Postsecondary • 1yr.
(Calcul différentiel, sciences de la nature)
Bonjour,
J'ai de la difficulté à trouver le domaine de la fonction suivante, car mes valeurs exclues (qui seront mes candidats à l'étude pour la, ou les, discontinuité.s) ne sont pas bonnes. Le domaine est supposé être:
IR\{7π/6 ; 11π/6}
Mais je trouve:
IR\{5π/3}
Ça fait un bout que je n'ai pas touché au cercle trigonométrique...pouvez-vous m'aider? Merci!
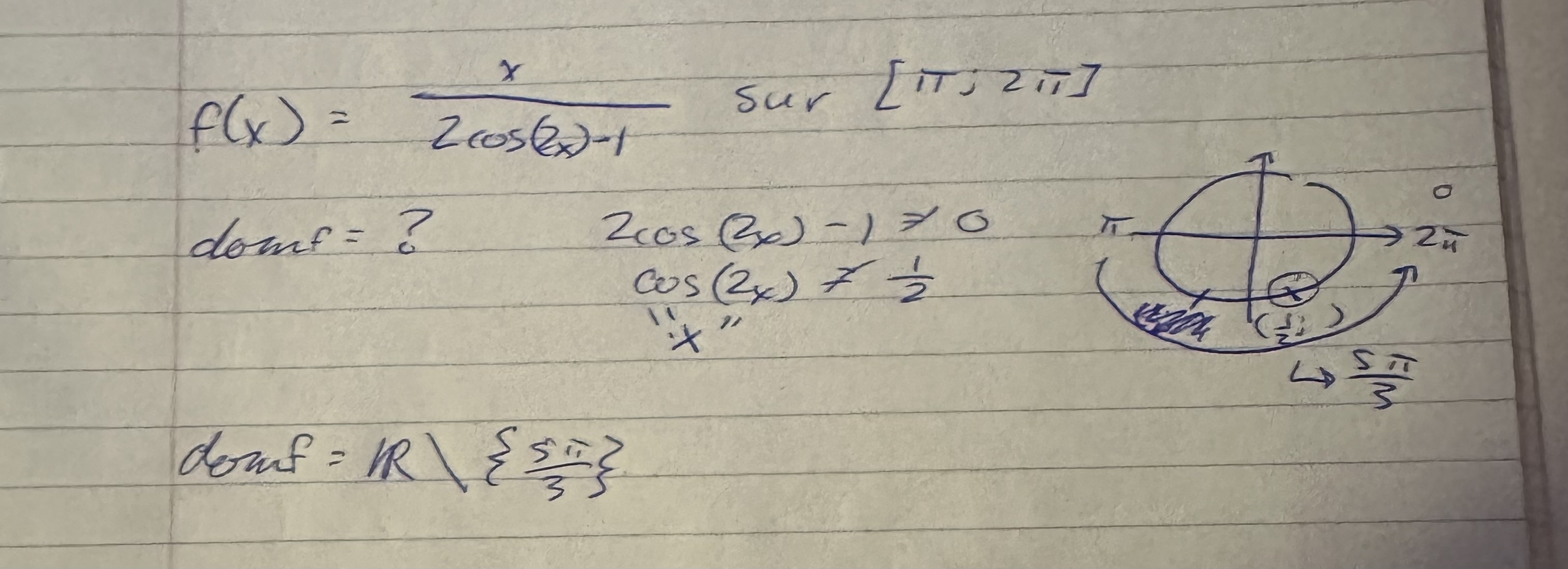






Explanation verified by Alloprof
This Explanation was verified by a member of the Alloprof team.
Le domaine doit être tel que π ≤ x ≤ 2π donc 2π ≤ x ≤ 4π
on doit aussi s'assurer que 2cos(2x) -1 ≠ 0
cos(2x) ≠ 1/2
dans le cercle trigonométrique cela signifie que 2x doit être différent de π/3 + k2π et 5π/3 + k2π, pour tenir compte de la période de 2π (note que pour 2π/3 et 4π/3 le cosinus est de -1/2)
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Ce qui revient à un x qui doit être différent de π/6 + kπ et 5π/6 + kπ
dans l'intervalle [π,2π] il y a π/6 + π = 7π/6 et 5π/6 + π = 11π/6 qu'on doit exclure
donc le domaine de la fonction est [π, 2π] \ {7π/6, 11π/6}
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.