Secondary V • 1yr.
Bonjour,
je n'arrive pas à comprendre ce problème mathématique. Est-ce que quelqu'un peux m'aider?
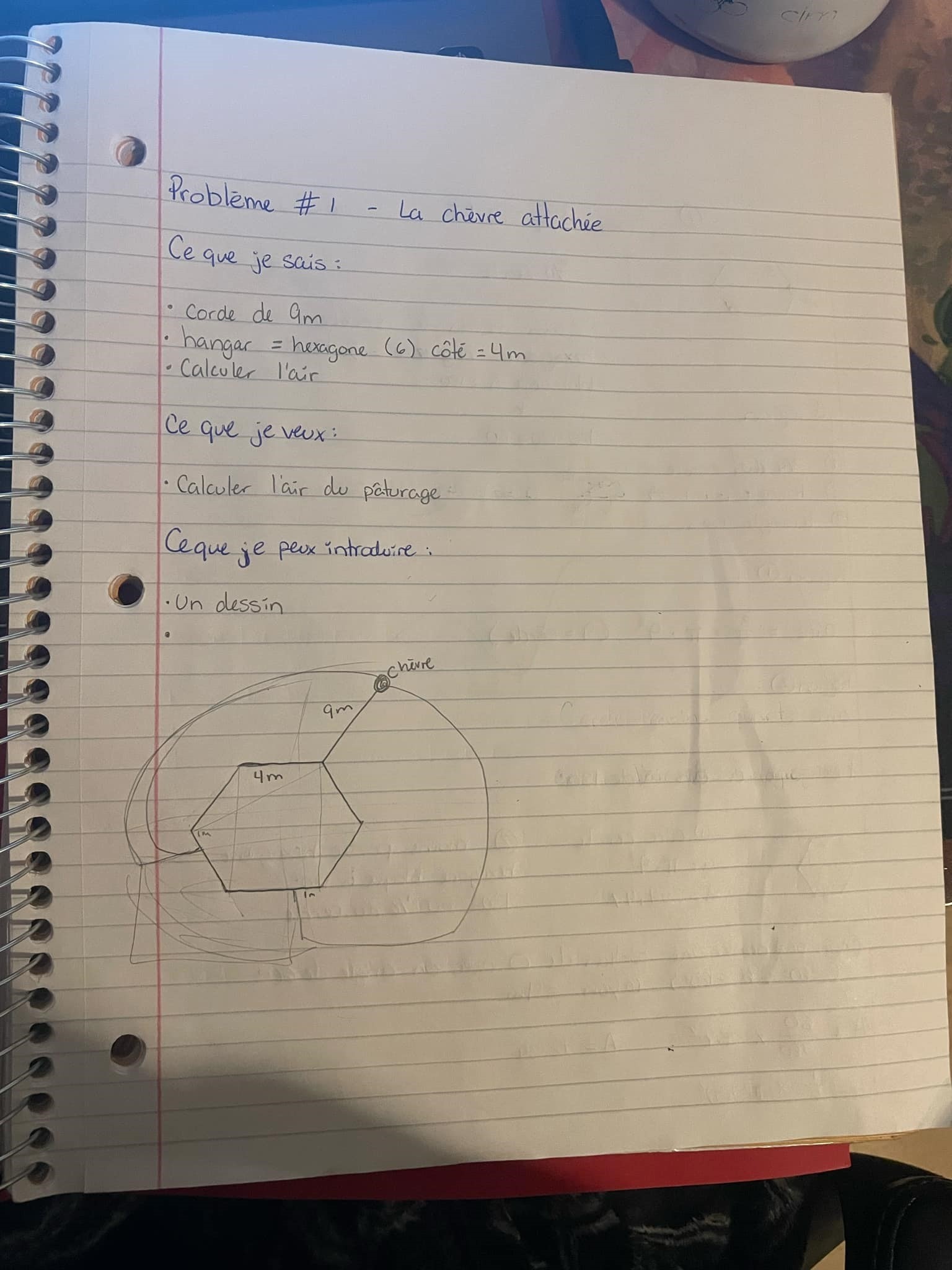
Une chèvre est attachée par une corde de 9 m au coin extérieur d’un hangar de la forme d’un hexagone régulier dont le côté mesure 4 m, situé dans un pâturage. Calculer l’aire de pâturage que la chèvre peut brouter.






Explanation from Alloprof
This Explanation was submitted by a member of the Alloprof team.
Bonsoir, DiplodocusOrange3310!
Tu as assez bien illustré la situation, félicitations!
On peut séparer l'aire atteinte en différents secteurs de disques.
Secteur 1
On calcule l'aire du premier secteur provenant d'un disque ayant comme rayon 9 m.
$$ \dfrac{\text{Angle au centre}}{360^\circ}=\dfrac{\text{Aire du secteur}}{\text{Aire du disque}} $$
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
«L'angle au centre» est en fait l'angle extérieur de l'hexagone. Pour le trouver, on calcule d'abord l'angle intérieur selon la formule ci-dessous, puis on soustrait cette valeur de 360 pour connaître l'angle externe.
$$ \begin{align}\text{Mesure d'un angle intérieur}&= \frac{\text{somme des angles intérieurs}}{\text{nombre de côtés du polygone}}\\ &= \frac{(n - 2) \times 180^\circ}{n}\end{align} $$
Secteur 2
Les deuxièmes secteurs ont un rayon de 5 m et un angle extérieur (l'angle compris entre un côté et le prolongement du côté adjacent) de l'hexagone.
$$ \begin{align}\text{Mesure d'un angle extérieur}&= \frac{360°}{\text{nombre de côtés du polygone}}\\ &= \frac{360°}{n}\end{align} $$
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Secteur 3
L'aire des derniers secteurs est calculée avec l'angle précédent, mais le rayon est de 1 m cette fois.
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
N'hésite pas à poser d'autres questions!