Bonjour!
J'avais des confusion sur la théorie des coniques qui me bloquent.
D'abord, je n'arrive pas à comprendre ce qu'est un foyer. Qu'est-ce qu'est le foyer, visuellement, physiquement et théoriquement? Mon enseignant fait souvent référance au cercle lorsqu'il explique le foyer, mais je suis tout de même bloquée. Je n'arrive vraiment pas à comprendre ce qu'il représente et comment il peut servir dans des calculs mathématiques :_(
Ensuite, en ce qui concerne la parabole, nous avons appris que la distance entre le foyer et un point de la parabole est la même que la distance entre ce même point et la droite directrice. Mais qu'est-ce qui explique cette corrélation? Comment prouver et démontrer que cette affirmation est vraie? Ça m'aiderait beaucoup si vous pourriez m'expliquer cette corrélation avec une démonstration mathématique?
Puis, j'aimerais juste comprendre comment et pourquoi l'équation de la parabole passe de:
à:
Je sais que c'est beaucoup de questions, mais je suis vraiment perdue. Ça m'aiderait beaucoup si vous m'expliquez avec détails, suivi d'illustrations, de graphiques et de démonstrations mathématiques si possible vu que je suis une personne très visuelle. Merci beaucoup!
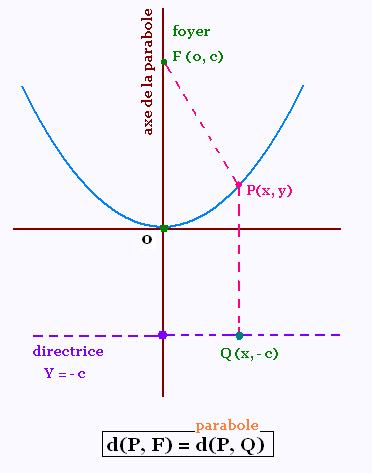
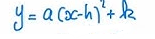
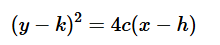






Pour prouver que d(P,F) = d(P,Q)
ou encore mFP = mPQ pour un point quelconque (x,y) sur la courbe
on a mFP² = (c-y)² + x²
et mPQ² = (y+c)²
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
donc mFP² = mPQ²
si et seulement si (qu'on représente par le symbole <=>)
(c-y)² + x² = (y+c)²
<=> c² -2cy + y² + x² = y² + 2cy + c²
<=> -2cy + x² = 2cy (après simplification)
<=> x² = 4cy
qui est vrai puisque c'est l'équation de la courbe: la parabole centrée à l'origine de foyer (0,c)
donc l'énoncé initial (d(P,F) = d(P,Q)) est vrai
Explanation verified by Alloprof
This Explanation was verified by a member of the Alloprof team.
L'équation
y = a(x - h)² + k (1)
est utilisée pour une parabole verticale de sommet (h,k)
or
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
https://www.alloprof.qc.ca/fr/eleves/bv/mathematiques/la-parabole-conique-m1330
il faut donc comparer cette équation (1) à
(x - h)² = 4c(y - k)
(x - h)²/(4c) = y - k
y = (x - h)²/(4c) + k
ce qui correspond en posant a = 1/(4c)
"Ensuite, en ce qui concerne la parabole, nous avons appris que la distance entre le foyer et un point de la parabole est la même que la distance entre ce même point et la droite directrice. Mais qu'est-ce qui explique cette corrélation? "
Ce n'est pas une corrélation, ce n'est pas aléatoire, c'est une relation.
Elle est bien illustrée ici (si j'ai le temps j'en ferai la démonstration plus tard)
https://www.alloprof.qc.ca/fr/eleves/bv/mathematiques/la-parabole-conique-m1330
Bonne chance !