Secondary IV • 8mo.
Bonsoir, je ne comprends pas comment vous arrivez à 0 quand f(x)= 72 car moi ça me donne 3. Pouvez-vous m'expliquer cela s'il vous plaît ? Aussi mes résultats sont les suivants:
Pente=1
Période=6
Valeur initiale (b) =3
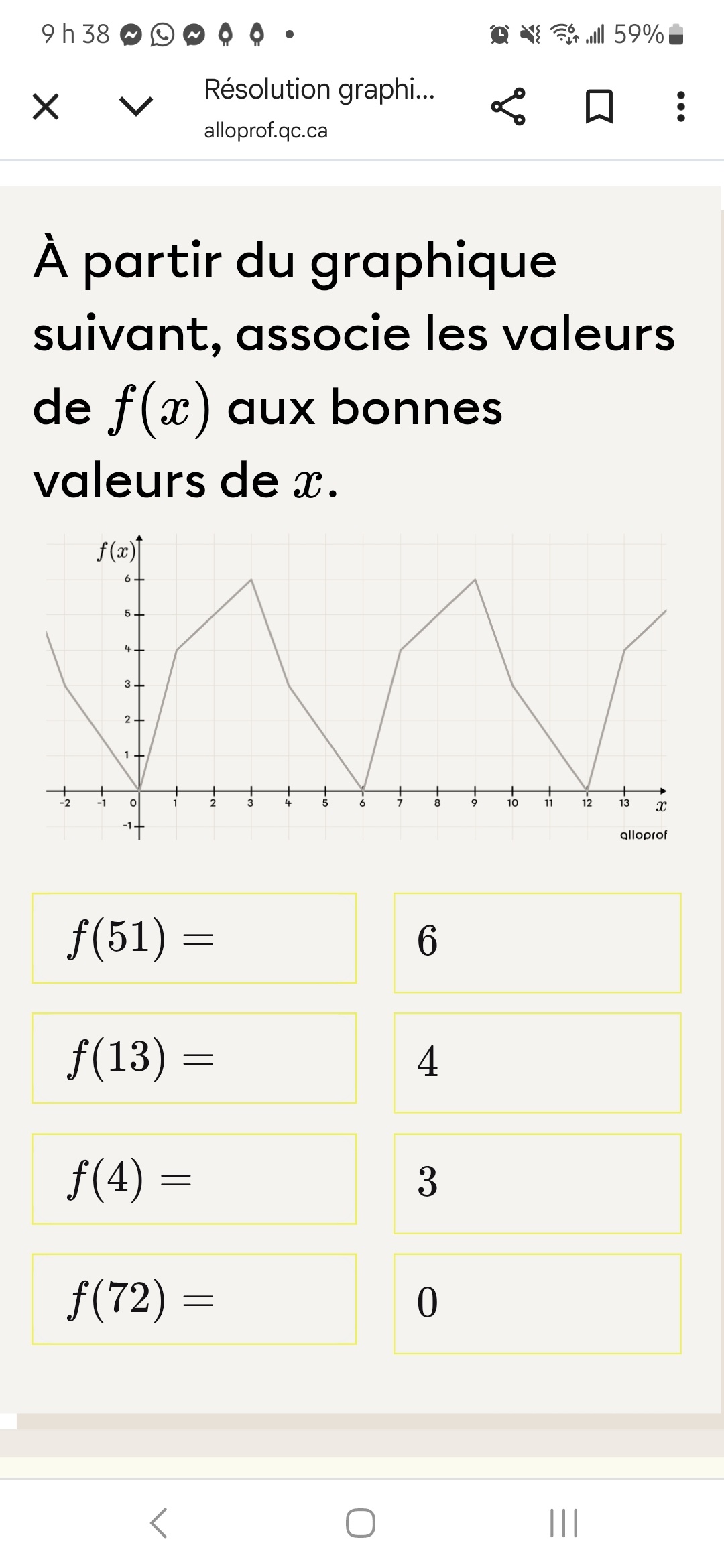
Pour la question qui est sur la photo j'ai eu tout mes résultats bon par rapport aux vôtres sauf celui de f(x)=72
Merci






Explanation from Alloprof
This Explanation was submitted by a member of the Alloprof team.
Salut!
Tu as une fonction périodique, c'est-à-dire une fonction où il y a un motif qui se répète à chaque cycle.
Ceci est 1 cycle complet :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
La période est donc bien de 6.
Cependant, la fonction n'a pas de pente ni de valeur initiale. En fait, chaque partie du motif périodique possède sa propre règle. En d'autres mots, la droite rouge possède une équation y=ax+b, la droite bleue aussi, la droite verte aussi, et la droite rose aussi.
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Il n'y a donc pas une seule pente et une seule valeur initiale pour l'ensemble de la fonction.
Ensuite, pour trouver f(72), c'est-à-dire la coordonnée en y du point à x=72, on doit trouver le point correspondant dans les cycles précédents, plus précisément ceux dans la partie visible du graphique donné. En d'autres mots, on va soustraire la période (6) jusqu'à ce qu'on soit avant x=13 afin de pouvoir trouver la réponse en observant le graphique :
$$72-6-6-6-6-6-6-6-6-6-6=12$$
On sait donc que f(72)=f(12). On peut trouver f(12) en regardant le graphique :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
On voit que la coordonnée en y du point à x=12 est de 0!
J'espère que c'est plus clair pour toi! :)