Bonjour!
J'ai deux cas que je veux clarifier avec vous concernant les situations liées aux graphiques de MRUA; les-voici:
Situation 1:
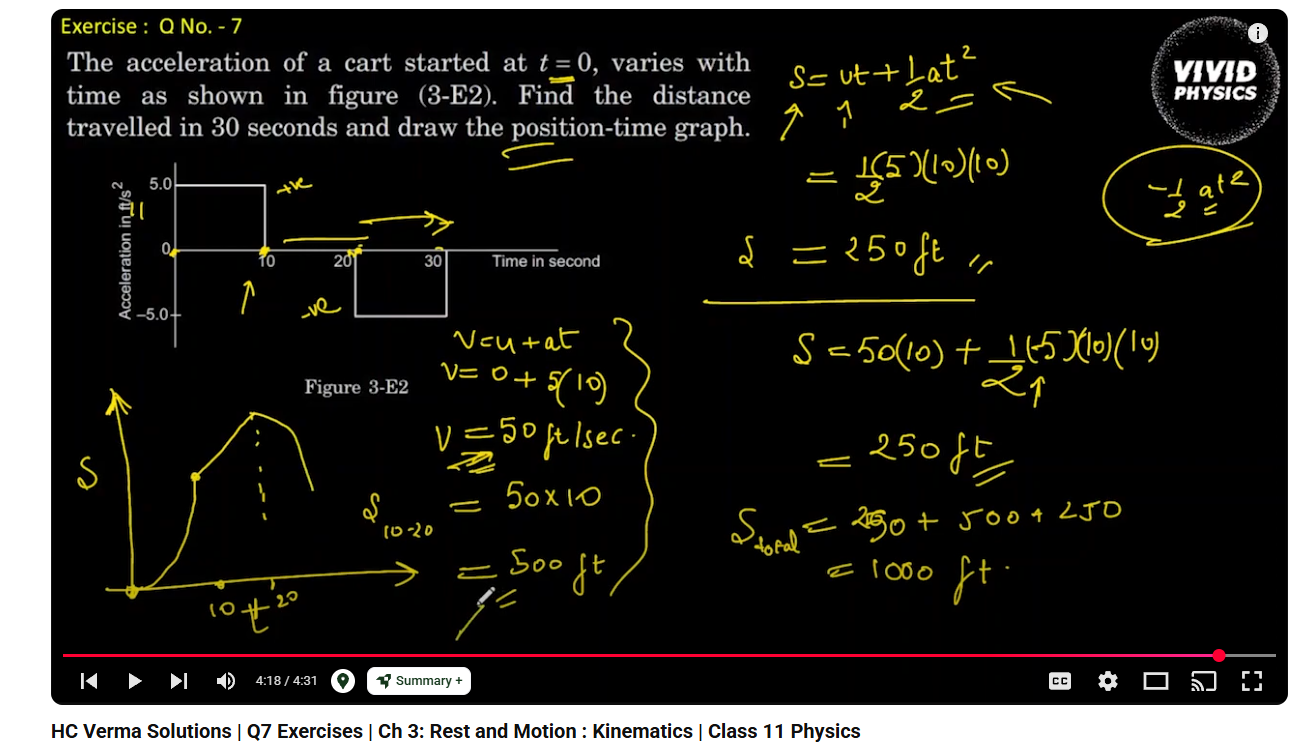
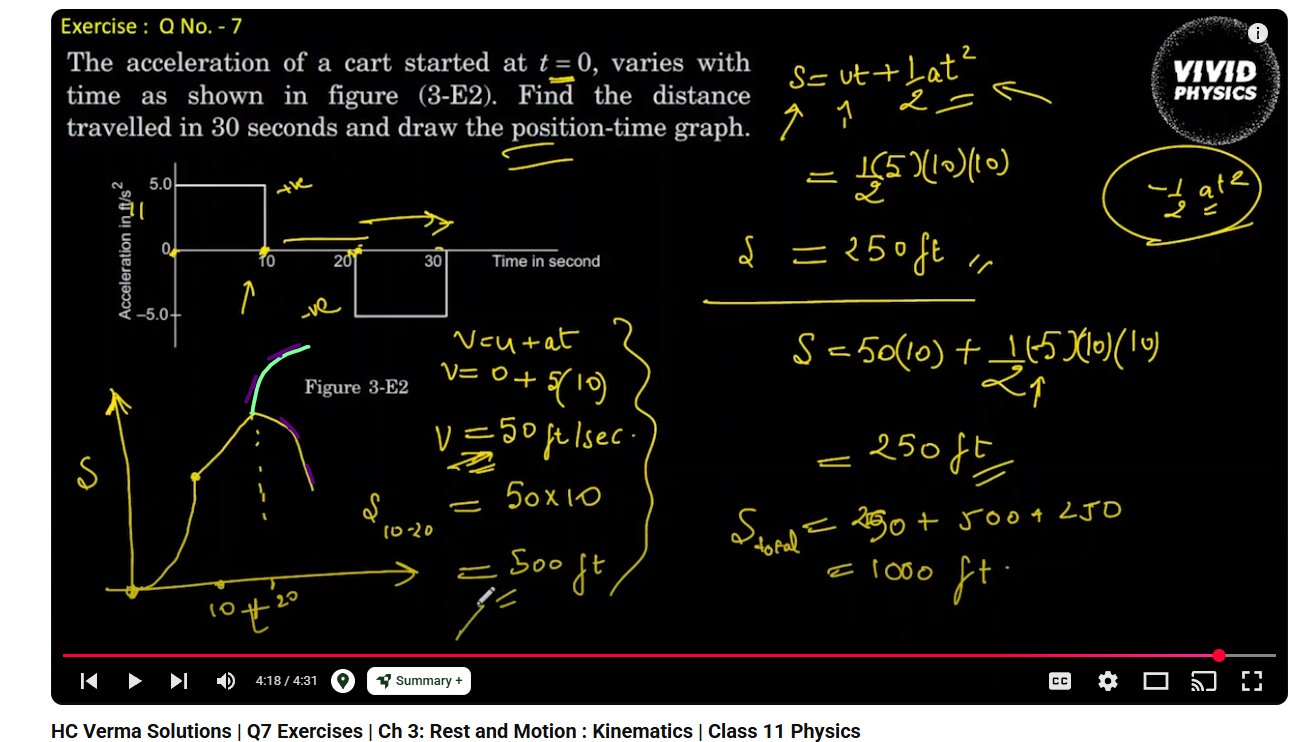
Je comprends que la personne a utilisé les formules de la cinétique pour trouver les déplacements, or je doute qu'il y a une erreur dans la dernière section de son graphique de position en fonction du temps. En fait, j'ai l'impression que le graphique à la fin devrait plutôt ressembler à ça, non?
Une autre question: comment savoir si le sens de déplacmeent est réellement positive ou négative et comment déterminer également le signe des vitesses si j'ai seulement un graphique de l'accélération?
Situation 2: https://youtu.be/7T-TPFnjjV8
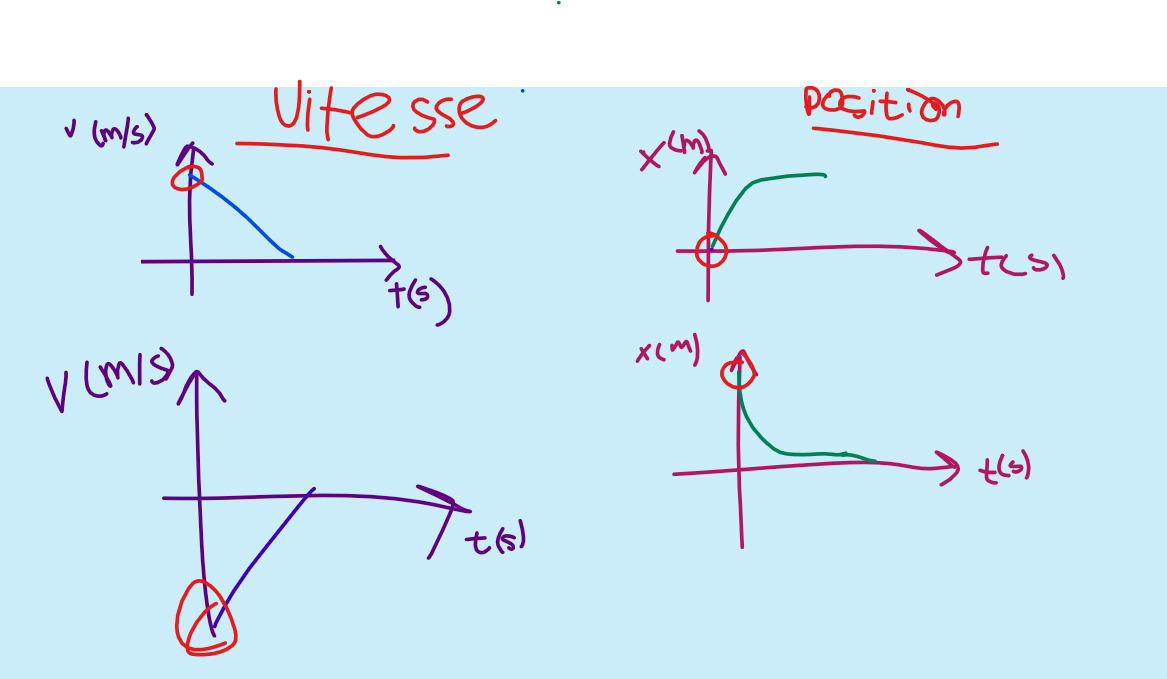
Dernière question, dans les minirécup de alloprof sur les graphiques de MRUA, j'avais une confusion par rapport au début du dessin de ces deux paires de graphique :
Pour la première paire de graphiques en haut (dans un cas où le déplacement est positive et l'objet avance, mais se ralentit), pourquoi est-ce que le graphique de la vitesse ne commence pas par l'origine ? Si on regarde le graphique de la position, est-ce que la tangeante au point à l'origine est nulle? SI oui, alors la vitesses instantanée au début du graphique de la vitesse devrait aussi commencer par l'origine, non?
Même chose pour la deuxième paire de graphique dans lequel l'objet recule et ralentit... La tangeante du premier point dans le graphique de la positon est également nulle, non? Donc, pourquoi le graphique de svitessesne comence pas de l'origine?
Merci énormément pour avoir clarifié ces doutes :)






Explanation from Alloprof
This Explanation was submitted by a member of the Alloprof team.
Salut!
Il y a en effet une erreur dans la dernière section du graphique, tu as bien raison, la parabole devrait être croissante, et non décroissante.
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
On peut le prouver en utilisant nos formules du MRUA.
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
De t=20 à t=30, on va chercher △x en utilisant cette formule :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
$$△x=v_{i}(30-20) + \frac{1}{2}(-5)(30-20)^2$$
$$△x=v_{i}(10) + \frac{1}{2}(-5)(10)^2$$
$$△x=10v_{i}+ \frac{1}{2}(-5)(100)$$
$$△x=10v_{i} + \frac{1}{2}(-500)$$
$$△x=10v_{i} -250$$
On a besoin de trouver \(v_{i}\), c'est-à-dire la vitesse initiale de ce mouvement, donc la vitesse à t=20, afin de trouver le déplacement.
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Je te laisse terminer les calculs. J'espère que c'est plus clair pour toi! :)
Bonjour CannebergeEnthousiaste9454,
Tout d'abord je me permets de te féliciter pour ton sens critique : tu ne sembles pas accepter tout ce qu'on te dit sans justification, tu te sers de ton jugement pour critiquer ce qu'on te donne. Et tu le fais à juste titre puisque... tu as entièrement raison.
Je commence par ta première figure. Tu as correctement identifié une erreur commise dans la réponse que tu nous as soumise : dans la dernière partie, il est exact que la courbe ne redescend pas mais plutôt qu'elle continue à monter mais à un rythme de moins en moins rapide.
Dans cette section, l'accélération négative représente une décélération mais un mouvement qui se continue dans le sens positif, exactement comme tu le proposes. Tu as 100% raison.
On pourrait aussi améliorer le graphique d'une autre façon : de la seconde 19,999 à la seconde 20,0001, si on veut faire un graphique parfait, il ne faudrait pas percevoir de changement de vitesse et par conséquent la pente du graphique ne devrait pas changer de façon perceptible. La vitesse constante de 20s à 30s devrait être identique à la vitesse finale du mouvement accéléré de 0s à 10s et devrait aussi être identique à la vitesse initiale du mouvement accéléré (ouais... décéléré, si tu préfères) de 20s à 30s. Il ne faudrait donc pas, en théorie, percevoir de changement de pente dans le graphique. Mais comme c'est difficile à respecter lorsqu'on trace une esquisse, c'est un détail qu'on néglige souvent. Je t'ai fait une illustration plus exacte pour t'aider.
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Pour ta deuxième question : c'est une question complexe qui mérite une réponse. En bref, ce qu'il faut techniquement faire, c'est lire le graphique de gauche à droite à partir de zéro et de calculer l'aire sous la droite de façon cumulée. Exemple : de 0s à 5s, l'aire est au-dessus de l'axe (donc positive), par conséquent la vitesse est positive. De 0s à 24s, il y a une aire positive de 50 et une aire négative de -20, ce qui donne une aire cumulative de 50-20=30, ce qui est positif, et on peut alors conclure que la vitesse est encore positive. À t=30s sur ce graphique, l'aire cumulative est égale à zéro, donc la vitesse est nulle. Elle pourrait devenir négative dans d'autres graphiques.
Pour tes autres questions :
1- «pourquoi est-ce que le graphique de la vitesse ne commence pas par l'origine ?» Réponse : parce qu'il est tout à fait possible d'étudier un objet qui est déjà en mouvement. S'il est déjà en mouvement au moment où on commence à l'étudier, alors la vitesse à t=0s n'est pas zéro. Cela ne cause aucun problème. Tu as le droit de partir ton chronomètre dans ton auto durant un voyage et étudier ce qui se passe à partir de cet instant.
2- «Si on regarde le graphique de la position, est-ce que la tangeante au point à l'origine est nulle?» Réponse : non, bien sûr, puisqu'il y a une vitesse initiale dans le graphique de vitesse
3- «SI oui, alors la vitesses instantanée au début du graphique de la vitesse devrait aussi commencer par l'origine, non?» Réponse : oui, tu as entièrement raison. Si la tangente du graphique position-temps est horizontale à t=0s, le graphique vitesse-temps doit partir de zéro.
Et c'est la même chose pour l'autre graphique, comme tu l'as fort justement fait remarquer.
En résumé, tu me sembles vraiment bien comprendre ces notions !