Populaires
Re : Question
Salut!
Oui, en effet des côtés homologues sont des côtés identiques.
Dans les statistiques, le caractère qualitatif signifie que l'information qu'on cherche ne peut pas être comptée (ce ne sont pas des nombres). Par exemple, la couleur préférée.
Quantitatif discret signifie que l'information recherchée est composée de nombres entiers. Par exemple, le nombre d'animaux de compagnie par élève.
Quantitatif continu signifie que l'information peut prendre différente valeurs dans intervalle donné. Par exemple, la taille d'un bébé à sa naissance. cette information (en nombres évidemment) va varier.
j'espère que c'est un peu plus clair, n'hésite pas si tu as d'autres questions:)
Re : Question
Salut!
Le degrès d'un terme, c'est son exposant et homologue signifie identiques.
J'espère que ça t'aide:)
Re : Question
Allo!
Les déterminants possessifs sont ceux qui démontrent à qui appartient quelque chose. Par exemple: Le garçon promenne son chien. Son est un déterminant possessif, le chien appartient au garçon.
Défini: Ce sont les déterminants qui montrent que l'on parle de quelque chose en précie. Par exemple: La fille joue dans le jardin. La est un déterminant définie, on parle d'une fille en précis.
Indéfini: C'est l'inverse des définis. On parle en général. Exemple: Des rues seront bientôt reconstruites. Des est un déterminant indéfini, on ne précise pas quelles rues.
Démonstratif: Déterminants qui démontrent quelque chose. Exemple: Cette semaine, j'irai au magasins. Cette démontre que c'est cette semaine que j'y irais.
Numéral: Tous les nombres et chiffres.
J'espère que ça t'est util:)
Question
Bonjour, Je ne comprend pas trop les ensembles de nombres ( Nb naturels N; Nb entiers Z; Nb rationnel; Nb irrationnels; Nb réels) est que vous pourriez m'aider a mieux comprendre ses termes. Merci
Re : Question
Bonjour!
Ici, on dit que les Algonquiens mettaient du bois dans l'eau pour le rendre plus mou et être capable de faire la courbe du du tobogan. En mettant le bois dans l'eau, le bois devenait plus facile à plier pour créer la sorte de demi-cercle qu'on retrouve à l'avant du tobogan, comme on voit sur l'image.
Si tu as d'autres questions, n'hésite pas à nous réécrire. Nous te répondrons avec plaisir!
Laurie :)
Re : Question
Allo ElfeSociable1552,
Merci pour ta question!
Techniquement, il y a plus de cours qui nécessite les SN4 comme préalable. Par contre, ça dépend de ton domaine. Comme tu n'es pas intéressé par les domaines scientifiques, tu n'as pas besoin de les avoir!
J'espère t'avoir aidé!
Lea-Kim
Re : Question
Salut :D
Peux-tu nous envoyer un exemple de problème que tu souhaites compléter en photo?
Ça nous aidera à mieux t'aider. :)
Tu connais le répertoire de révision, ça pourrait bien t'être utile.
À tout de suite :D
Re : Question
on pose x, y les deux nombres en question
x+y=1 x,y réels
S(x,y)=2y^2+x^3
on doit trouver un maximum local de la somme S(x,y)
y=1-x
S(x,y)=2(1-x)^2+x^3
S(x,y)=2(x^2-2x+1)+x^3
S(x,y)=x^3+2x^2-4x+2
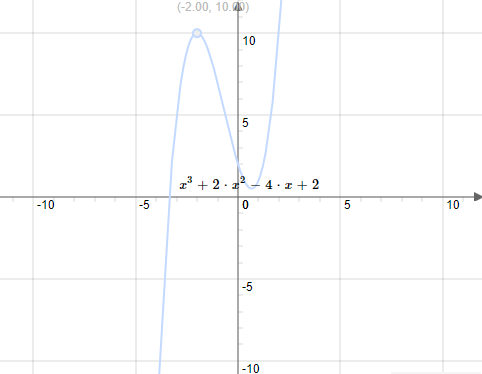
on pose f(x)=x^3+2x^2-4x+2
polynôme du 3 degré
f'(x)=3x^2+4x-4
f'(x)=0 deux solutions x=-2 ou x=2/3
f'(x)=3(x+2)(x-2/3)
Signe de f'(x)
]-∞, -2 [ f'(x) strictement positive, f est croissante
]-2, 2/3 [ f'(x) strictement négative, f est décroissante
]2/3, +∞ [ f'(x) strictement positive f est croissante
x=-2 f'(-2)=0, tangente horizontale
donc en x=-2 on a un extremum local
x=2/3 f'(2/3)=0, tangente horizontale
donc en x=2/3 on a un minimum local
limite f(x) quand x tend vers -∞ = -∞
limite f(x) quand x tend vers +∞ = +∞
d'après le graphe
x=-2 on a un extremum local
f(-2)=(-2)^3+2(-2)^2-4(-2)+2
f(-2)=10
pour x=-2 on obtient y=3
donc pour le couple (-2,3) est solution
S(x,y)=2y^2+x^3
S(-2,3)=2(3)^2+(-2)^3
S(-2,3)=18+(-8)=10
Re : Question
Après 495 il y a: 496, 497, 498.
Est-ce bien la question que tu voulais poser?