Populaires
Re : Question
Bonjour CyborgAlerte,
Merci de faire appel à nos services! :)
Habituellement, au deuxième cycle (sec 3, sec 4 et sec 5), c'est par matière. Alors, si tu coules mathématiques, par exemple, tu redoubleras mathématiques secondaire 3 seulement. Pour les autres matières, tu monteras en secondaire 4.
N'hésite pas à nous réécrire si tu as d'autres questions! :)
Marilee
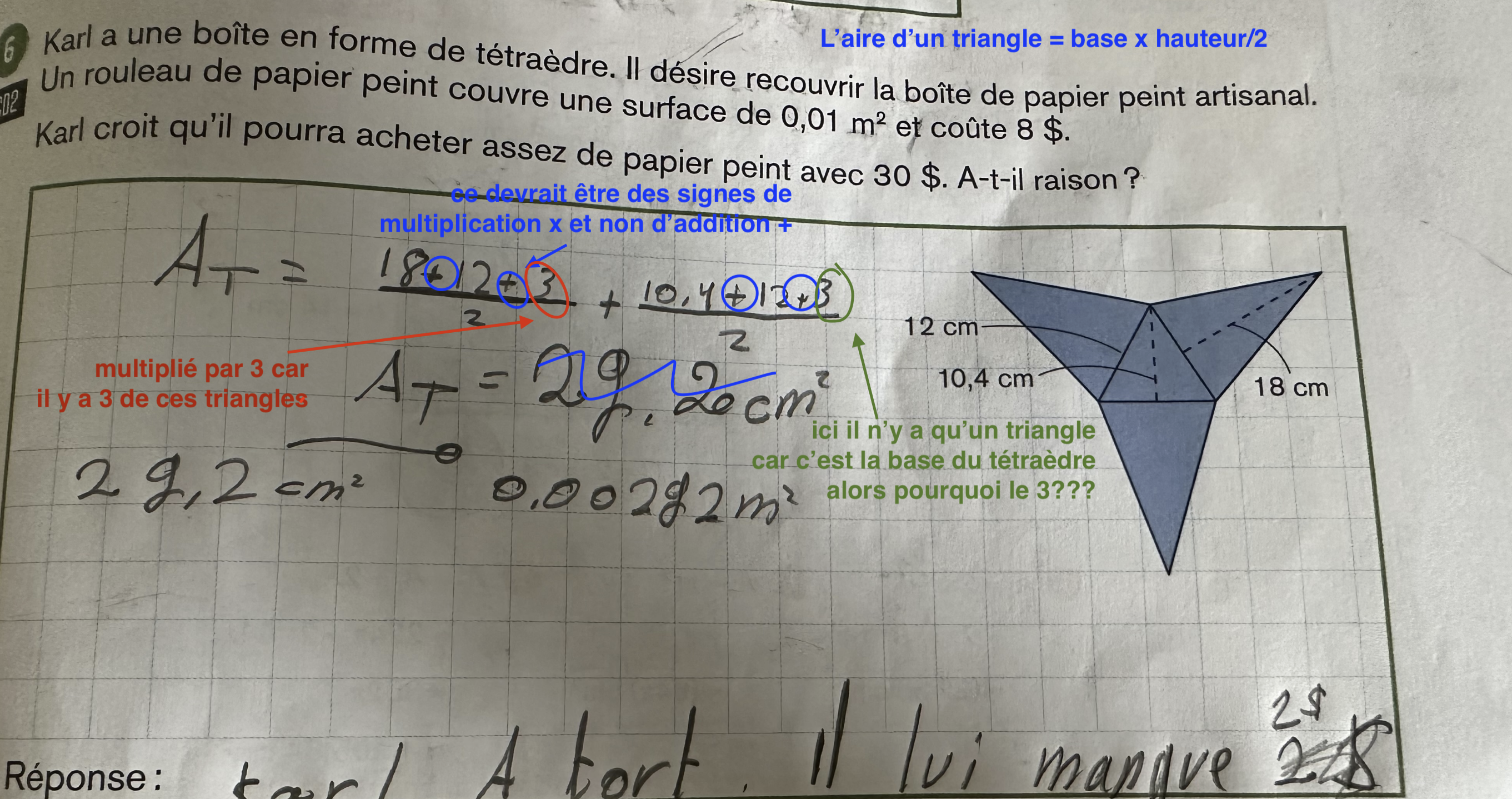
Re : Question
Tu as confondu signes de multiplication et signes d'addition. (Distraction? mauvaise écriture?)
Ton calcul de prix, basé sur la surface trouvée, m'intrigue
si pour 0.01 m² il en coûte 8$
alors pour 0.00292 m² il en coûtera 0.00292 x 8 / 0.01 = 2.34$
alors avec 30$ il aurait bien assez d'argent.
Re : Question
Bonjour,
D'abord, 60$/h est équivalent à 1$/min. C'est déjà une seule contrainte. Rappelle-toi que dans une heure il y a 60 minutes.
Ainsi, tu peux choisir le moyen que tu veux de l'écrire. Prends le moyen le plus avantageux qui allégera tes calculs.
N'hésite pas si tu as d'autres questions!
Re : Question
Ce problème d'optimisation est un peu différent de ceux que l'on voit en général.
soit x = le prix d'un oiseau
et y = le nombre de ventes d'oiseau par semaine
On suppose que la diminution des ventes est proportionnelle à l'augmentation des prix ce qui veut dire que
∆y / ∆x = k = (40 - 24)/(25-35) = -1.6 qui est aussi la pente de la droite y = mx + b
par ailleurs quand x = 50, y = 0 donc 0 = -1.6 · 50 + b et b = 80
donc la relation entre x et y est: y = -1.6x + 80
Par ailleurs on veut maximiser le profit
profit = y ( x - 4.50)
= (-1.6x + 80) (x - 4.50) = -1.6x² + 87.2x - 360
Les seules restrictions sont x≥ 0 et profit ≥ 800
cette dernière restriction donne
-1.6x² + 87.2x - 360 ≥ 800
et donc -1.6x² + 87.2x - 1160 ≥ 0
pour maximiser l'expression il faut trouver le x≥ 0 tel que la parabole est à son maximum - comme c'est une parabole verticale, un U à l'envers, son sommet est le maximum recherché.
En trouvant les zéros de la parabole, tu as ton point milieu et ton sommet.
Re : Question
Bonjour,
vous pouvez lui dire par exemple de faire ceci
prend 51- 3= 45
45-3 = 42
42-3 = 39
39-3= 36
ici il ya bcp plus d’essai Erfurt malheureusement
Re : Question
Note que si les données de départ avaient été disponibles, une moyenne de tous les âges aurait été la réponse idéale. La moyenne en utilisant le point milieu de chaque intervalle, pondéré par le nombre de personnes dans l'intervalle, est la meilleure approximation dans les circonstances.
Re : Question
Tu peux aussi commencer avec des valeurs simples
pour la fonction en (c) et le premier graphique -- qui est le bon, en passant --
f(x) = 2cos π(x+1) - 1
pour x = 0, f(0) = 2cos π(1) - 1 or cos π = -1 donc
f(0) = 2(-1) - 1 = -2 - 1 = -3
pour x = 2, f(2) = 2cos π(3) - 1 or comme le cycle du cosinus est 2π cos 3π = cos π
et f(2) = -2 - 1 = -3
Re : Question
Bonjour,
Tu as raison, la règle C correspond au graphique 1.
Ainsi, tu as seulement fait une erreur de frappe sur la calculatrice. Lorsque tu as entré les données, tu ne t'es pas assuré que le π x (2+1) soit à l'intérieur du cos, tu as juste entré le π et par après tu as multiplié par 3, ce qui est mauvais.
Tu devrais taper 2cos(π(2+1))-1 et avoir -3 comme réponse. N'oublie pas que la calculatrice aussi respecte la priorité des opérations.
N'hésite pas si tu as d'autres questions!
Re : Question
Une inéquation est une inégalité qui contient une inconnue x. Résoudre une inéquation, c'est trouver toutes les valeurs de x qui vérifient cette inégalité. Il s'agit d'un ensemble de valeurs. Les solutions sont tous les nombres
-strictement inférieurs à
-strictement supérieurs à
-inférieurs ou égal à
-supérieurs ou égal à
Re : Question
Bonjour,
Pour résoudre une équation ou une inéquation du premier degré, il est possible d'utiliser différentes méthodes générales (la balance, les opérations inverses, le terme caché et l'essai-erreur). Ces méthodes sont expliquées dans la fiche suivante.
Il y a même des vidéos, regarde-les!
Pour résoudre une inéquation, on procède sensiblement de la même façon que pour résoudre une équation: on isole la variable désirée. La différence entre les équations et les inéquations réside dans le signe d’inégalité.
Pour résoudre une inéquation, il est primordial de se rappeler qu'il faut appliquer les mêmes manipulations à gauche et à droite de l’égalité.
Lorsque l’on divise ou que l’on multiplie par un nombre négatif, on doit changer le sens du signe d'inégalité.
Pour plus d'explications et d'exemples, consulte la fiche suivante.
N'hésite pas si tu as d'autres questions!