Secondaire 5 • 2a
Bonjour, pouvez-vous m'aider!
J'ai commencé par faire comme si les points (9,32) et (3,8) étaient une droite. Alors j'ai trouvé leur équation qui me donne y=4x-4 et là je suis bloqué je ne sais plus quoi faire.






bonsoir,
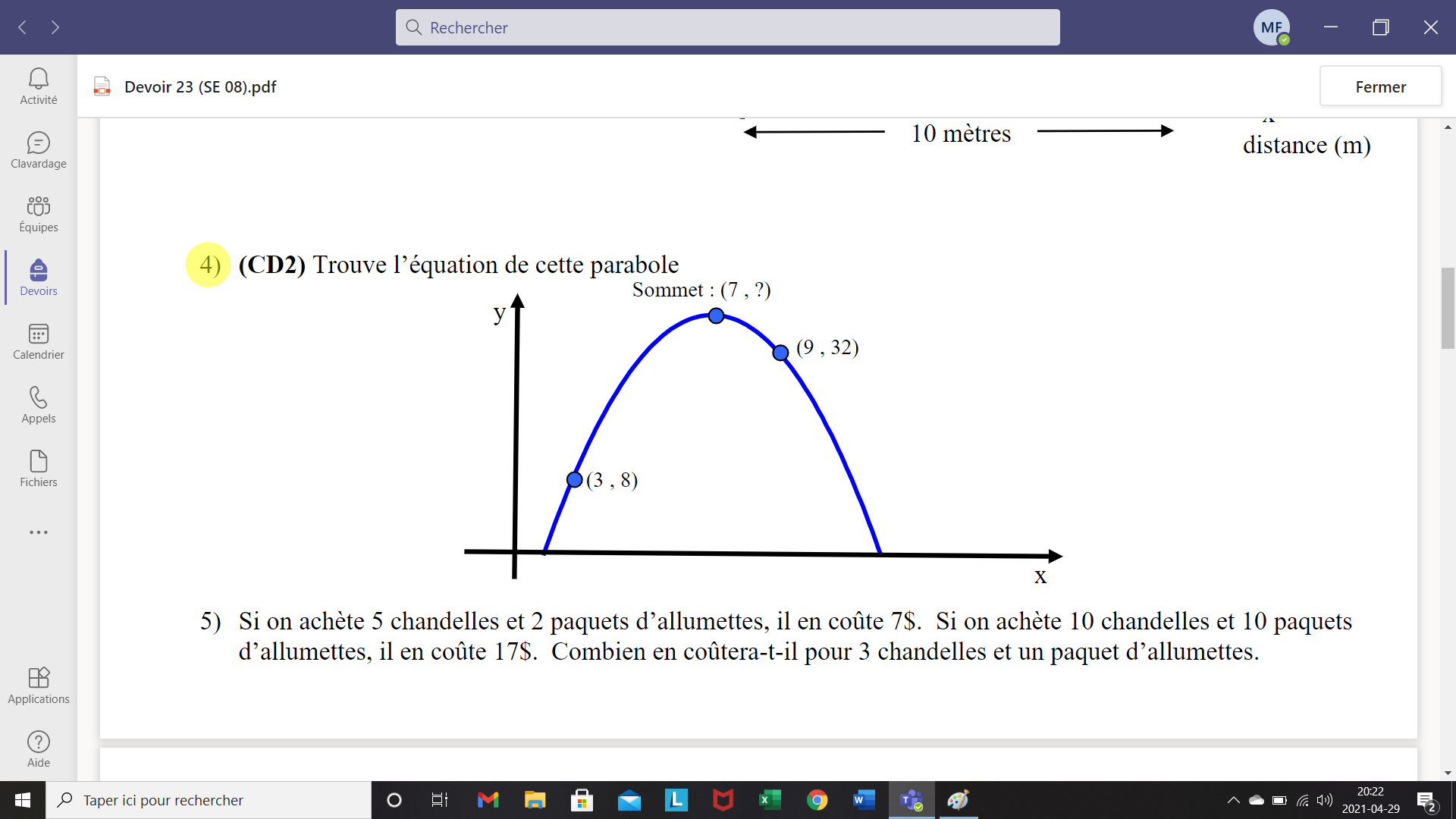
La règle est de la forme y=a(x-h)²+k.
Le sommet de la parabole te donne h=7.
D'où y=a(x-7)²+k.
Avec les coordonnées du point (3,8) tu écris cette équation : 8=a(3-7)²+k qui devient 8=16a+k.
Tu fais pareil avec l'autre point et tu résous le système d' équations pour déterminer la valeur de a et k.
Tu termines en donnant la règle (l'équation) de la parabole.
Note: quand j'ai commencé à écrire mon explication, celle de Simon n'était pas là!
Explication d'Alloprof
Cette explication a été donnée par un membre de l'équipe d'Alloprof.
Salut,
c'est l'équation d'une parabole, pas d'une droite.
L'équation sous forme canonique est \[f(x) = a(x -h)^2 + k\]
Ici, on connaît l'abscisse du sommet, c'est-à-dire que \(h = 7\), mais on n'a ni la valeur de \(a\), ni la valeur de \(k\).
Ce qu'on peut faire, c'est remplacer \(x\) et \(y\) deux fois par les coordonnées des deux autres points, \((3, 8)\) et \((9,32)\).
\begin{align*}32 &= a(9-7)^2 + k \\ \\ 8 &= a(3-7)^2 + k\end{align*}
Si on simplifie un peu, on obtient \begin{align*}32 &= a\cdot 2^2 + k \\ \\ 8 &= a\cdot (-4)^2 + k\end{align*}
et enfin \begin{align*}32&= 4a + k \\ \\ 8 &= 16a + k\end{align*}
Là tu peux résoudre le système d'équations (comparaison, substitution, réduction). Cela te donnera les valeurs de \(a\) et de \(k\).
À toi de jouer !
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!