Expressing a Fraction as a Mixed Number and Vice Versa

1. Divide the numerator by the denominator. The result will consist of an integer and a remainder.

2. Write the integer followed by a fraction whose numerator is the remainder and whose denominator is the same as that of the original fraction.

Express |\displaystyle \frac{14}{5}| as a mixed number.

1. Divide the numerator by the denominator.

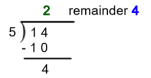
The result consists of an integer (|\color{green}{2}|) and a remainder (|\color{blue}{4}|).

2. Write the integer followed by a fraction whose numerator is the remainder and whose denominator is the same as the original fraction.

Therefore, the fraction |\displaystyle \frac{14}{5}| can be expressed as the mixed number |\displaystyle 2\frac{4}{5}|.

1. Express the integer of the mixed number as a fraction with a denominator of |1|.

2. Add this fraction and the fractional part of the mixed number.

Express |\displaystyle 4\frac{2}{3}| as a fraction.

1. Express the integer of the mixed number as a fraction with a denominator of |1|.

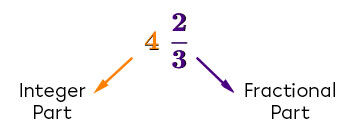
Expressing the integer as a fraction results in the following: |\displaystyle4\Rightarrow \frac{4}{1}|

2. Add this fraction and the fractional part of the mixed number.
   ||\begin{align}\frac{4}{1}+\frac{2}{3}&=\frac{4\color{red}{\times 3}}{1\color{red}{\times 3}}+\frac{2}{3}& &(\text{Put on the same denominator})\\
   &=\frac{12}{3}+\frac{2}{3}\\
   &=\frac{14}{3}\end{align}||
   Therefore, |\displaystyle 4\frac{2}{3}| is equivalent to the fraction |\displaystyle \frac{14}{3}|

1. Multiply the integer of the mixed number by the denominator of its fractional part and then add this result to the numerator.

2. Write the final result of step 1 as the numerator of a fraction whose denominator is the same as the fractional part.

Express |8\;\displaystyle \frac{3}{7}| as a fraction.

1. Multiply the integer of the mixed number by the denominator of its fractional part and then add this result to the numerator.
   In this example, the integer is |8|, the denominator is |7|, and the numerator is |3|. Thus, the following result is obtained: ||8\times 7+3=59||

2. Write the final result of step 1 as the numerator of a fraction whose denominator is the same as the fractional part of the mixed number.
   The result is |59| and the denominator is |7|. Thus, the final result is: ||\displaystyle 8\;\displaystyle \frac{3}{7}=\frac{59}{7}||

Think of this procedure as resembling a wheel because the order of operations is performed in a circular movement.

Let's take the example above and analyze the operations.

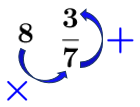
The circular movement enables the mixed number to be expressed as a fraction.
||\displaystyle \frac{8\color{blue}{\times}7\color{blue}{+}3}{7}=\frac{59}{7}||
This is a great way to remember this method!