Finding the Rule of a Logarithmic Function

The values of |b| and |c| are known

Find the equation of the logarithmic function that passes through the point |(5, -3)| if the value of the parameter |b| is |2| and the value of the base |c| is |10|.

Replace |\color{blue}{b}|, |\color{red}{c}|, |\color{green}{x}|, and |\color{purple}{y}| in the equation.
||\begin{align}\color{purple}{y} &= a \log_{\color{red}{c}} \big(\color{blue}{b}(\color{green}{x})\big)\\ \color{purple}{-3} &= a \log_{\color{red}{10}} \big(\color{blue}{2} \times \color{green}{5}\big)\\-3 &= a \end{align}||
Answer: the equation is |y=-3 \log \big(2(x)\big).|

The values of |a| and |c| are known

Find the equation of the logarithmic function passing through the point |(-12, 8)| if the value of the base |c| is |2| and the parameter |a| is |-4|.

Replace |\color{magenta}{a}|, |\color{red}{c}|, |\color{green}{x}|, and |\color{purple}{y}| in the equation.
||\begin{align}\color{purple}{y} &= \color{magenta}{a}\log_{\color{red}{c}} \big(b(\color{green}{x})\big)\\ \color{purple}{8} &= \color{magenta}{-4} \log_{\color{red}{2}} \big(b \times \color{green}{-12}\big) \end{align}||
Isolate the expression containing the logarithm.
||-2 = \log_2 (-12b)||
Switch to exponential form to isolate |b|.
||\begin{align}2^{-2} &= -12b\\ \dfrac{2^{-2}}{-12} &= b\\ \dfrac{\text{-}1}{48}&=b \end{align}||
Answer: the equation is |y= -4 \log_2 \left(\dfrac{\text{-}1}{48}(x) \right).|

The value of |a| is known

Find the equation of a logarithmic function that goes through the points |(0.25; -4)| and |(128, 8).|

Let the parameter |a| equal |4|. Replacing |a| with |4,| results in the equation |y= 4 \log_c \big(b(x)\big).|

Replace |x| and |y| with the coordinates in the equation.

The result is |-4 = 4 \log_c (b \times 0.25)| and |8 = 4 \log_c (b \times 128).|

Next, isolate |b| in both equations.
For the first equation:
||\begin{align}-1 &= \log_c (0{.}25b)\\c^{-1} &= 0.25b\\ \dfrac{c^{-1}}{0.25}&=b \end{align}||
For the second equation:
||\begin{align}2 &= \log_c (128b) \\ c^{2} &= 128b\\ \dfrac{c^{2}}{128} &= b \end{align}||
Next, use the comparison method.
||\dfrac{c^{-1}}{0.25} = \dfrac{c^{2}}{128}||
Rearrange the fractions:
||\begin{align} \dfrac{128}{0.25} &= \dfrac{c^2}{c^{-1}}\\ 512 &= c^3\\ \sqrt[3]{512} &= \sqrt[3]{c^3}\\ 8 &= c \end{align}||
Therefore, the result is that the base |c=8.|

Simply replace |c| in one of the starting equations to find the value of |b.|
||b = \dfrac{c^{-1}}{0.25} = \dfrac{8^{-1}}{0.25} = \dfrac{1/8}{1/4} = \dfrac{1}{2}\\ b = \dfrac{c^2}{128} = \dfrac{8^2}{128} = \dfrac{64}{128} = \dfrac{1}{2}||
Answer: The equation of the function is |y= 4 \log_8 \left(\dfrac{1}{2}(x)\right).|

When the value of a single parameter is known, the best approach is to use the coordinates of two points located on the curve. Then, use the comparison method.

There are two ways to express the equation of a logarithmic function in standard form.

||y= \log_c \big(b(x-h)\big)||

OR

||y= \log_c (\pm(x-h)) + k||

Consider the following concrete example.

||\begin{align} y &= \log_c \big(b(x-h)\big) && \text{first standard form}\\\\ &= \log_2 \big(-16(x-8)\big) && \text{equation we are working with}\\\\ &= \log_2 16 + \log_2 (-(x-8)) && \text{logarithm of a product} \\\\ &= 4 + \log_2 (-(x-8))&& \text{calculating the logarithm}\\\\ &= \log_2 (-(x-8)) + 4 && \text{rearranging the terms} \\\\ y &= \log_c (\pm(x-h)) + k && \text{second standard form} \end{align}||

In a logarithmic function, there is a multiplying factor at work with each change in the independent variable when the dependent variable increases by |1|. This multiplying factor corresponds to the base |c| of the function.

Here is a table of values of the function |y=\log_9 x.|

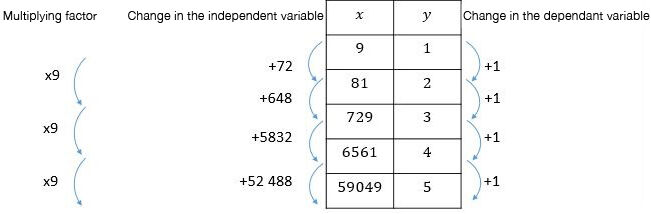
Note that the multiplying factor is |9|, which corresponds to the base |c| of the function |y=\log_9 x.|

Here are the steps to follow in order to find the equation of a logarithmic function in the form |y= \log_c \big(\pm(x-h)\big)+k .|

1. Find the value of the base |c| by finding the multiplying factor.

2. Depending on the value of the base |c|, determine whether to use the + or the - in the bracket.

3. Replace |x| and |y| in the equation of the function with the coordinates of 2 points.

4. Isolate the parameter |k| in both equations.

5. Use the algebraic comparison method to find the value of parameter |h.|

6. Replace |h| in either of the two equations to find the value of parameter |k.|

Here is the table of values of a logarithmic function.

1. Find the value of the base |c| by finding the multiplying factor

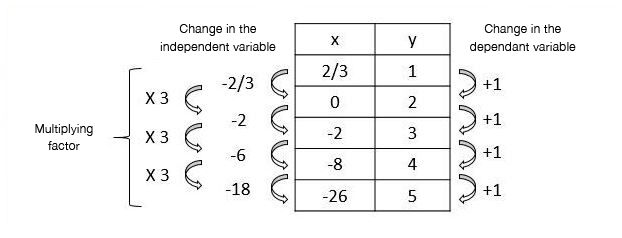
Therefore, the base is |c=3.|

2. According to the value of the base |c|, determine whether to use the + or the - in the bracket
   
   In this case, the more the values of |x| increase, the more the values of |y| decrease. Since the function is decreasing and the value of the base |c| is greater than |1|, use the sign |-| in the bracket. ||\begin{align} y &= \log_{\color{magenta}{c}} (\color{red}{\pm}(x-h))+k\\ y &= \log_{\color{magenta}{3}} (\color{red}{-}(x-h))+k\end{align}||

3. Replace |x| and |y| in the equation of the function by 2 points
   
   Take the points |(0, 2)| and |(-8, 4)| and insert them into the equation. ||\begin{align} 2 &= \log_3 (-(0-h))+k\\ \Rightarrow\ 2 &= \log_3 (h) +k \\\\ 4 &= \log_3 (-(-8-h))+k \\ \Rightarrow\ 4 &= \log_3 (8+h) +k\end{align}||

4. Isolate the parameter |k| in both equations
   
   The result is the following |2- \log_3 (h) = k| and |4-\log_3 (8+h) = k.|

5. Use the algebraic comparison method to find the value of parameter |h|
   ||\begin{align} 2 - \log_{3}{(h)} &= 4 - \log_{3}{(8+h)}\\\\ 2 - 4 &= -\log_{3}{(8+h)} + \log_{3}{(h)} \\\\ -2 &= \log_{3}{(h)} - \log_{3}{(8+h)} && \text{Rearranging the logarithms}\\\\ -2 &= \log_{3}\left(\dfrac{h}{8+h}\right) && \text{Logarithm of a quotient}\\\\ 3^{-2} &= \dfrac{h}{8+h} && \text{Use exponential laws}\\\\ \dfrac{1}{3^{2}} &= \dfrac{h}{8+h} && \text{Definition of a negative exponent} \\\\ \dfrac{1}{9} &= \dfrac{h}{8+h} \\\\ 8+h &= 9h && \text{By cross multiplication} \\\\ 8 &= 8h \\\\ h &= 1 \end{align}||

6. Replace |h| in either of the two equations to find the value of the parameter |k| 
   ||\begin{align}
   4 &= \log_3 (-(-8-h))+k \\\\
   4 &= \log_3 (-(-8-1)) + k && \text{Replace } h \text{ with its value} \\\\
   4 &= \log_3 (9) + k\\\\
   4 &= 2 + k && \text{Calculate the logarithm}\\\\
   2&=k \end{align}||

Therefore, the conclusion is that the equation of the logarithmic function is |y= \log_3 (-(x-1))+2.|

1. Replace |h| with the value of the asymptote.

2. Substitute in each of the points to create a system of equations.

3. Find the value of the base |c| using the comparison method.

4. Use one of the two equations from step 2 to find the value of the parameter |b.|

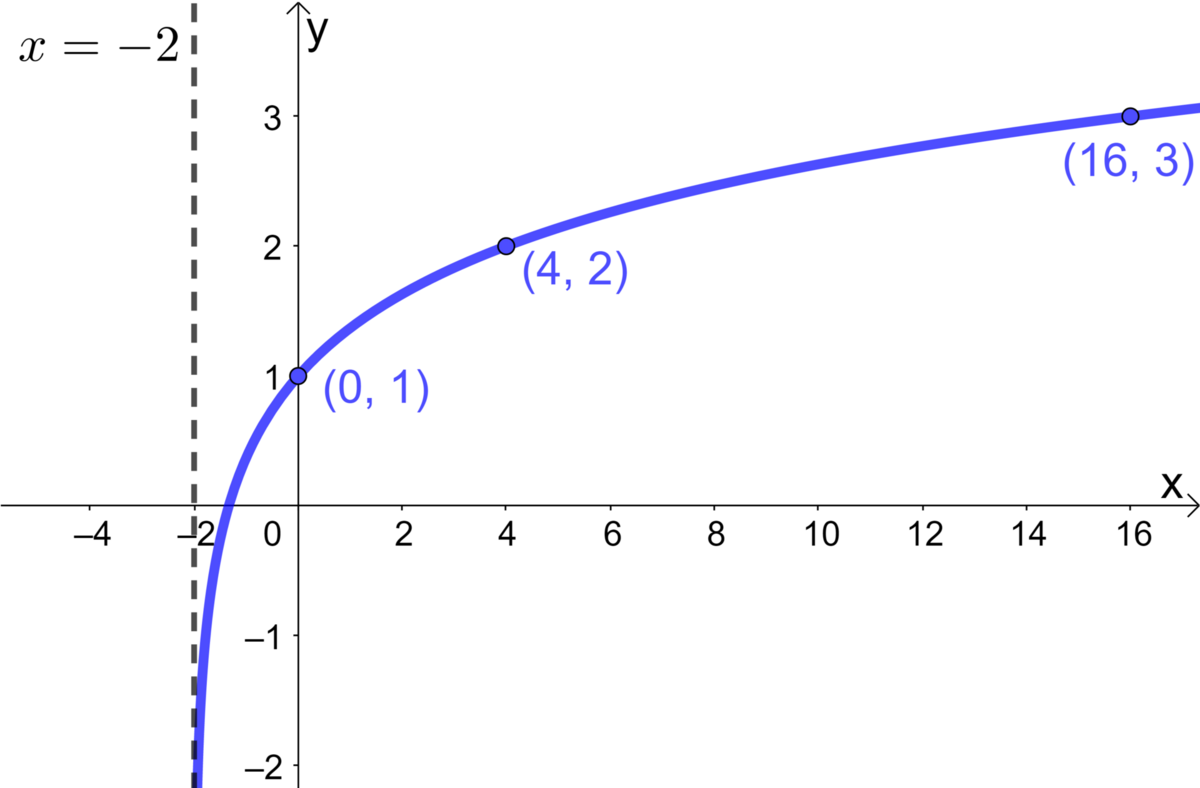
1. Replace |h| with the asymptote’s value||\begin{align} y &= \log_c \big(b(x-\color{green}{h})\big) \\y &= \log_c \big(b(x-\color{green}{\text{-}2})\big) \\y &= \log_c \big(b(x\color{green}{+2})\big) \\ \end{align}||

2. Substitute in each of the points to create a system of equations

||\begin{align} &1^{\text{st}}\text{ coordinate pair: }(0,1) && 2^{\text{nd}}\text{ coordinate pair: }(16,3) \\\\ y &= \log_c \big(b(x+2)\big) && y = \log_c \big(b(x+2)\big) \\\\ 1 &= \log_c \big(b(0+2)\big) && 3 = \log_c \big(b(16+2)\big) && \text{Substitute in } x \text{ and } y \\\\ 1 &= \log_c (2b) && 3 = \log_c (18b) \\\\ c^1 &=2b && c^3 =18b \\\\ \dfrac{c}{2} &= b && \dfrac{c^3}{18} = b && \text{Isolate } b \end{align}||

3. Find the value of the base |c| using the comparison method||\begin{align} b & = b \\\\ \frac{c}{2} & = \frac{c^3}{18} \\\\ \frac{18}{2} & = \frac{c^3}{c} \\\\ 9 & = c^2 && \text{exponent properties} \\\\ \sqrt9 & = \sqrt{c^2} \\\\ 3 & = c\end{align}||

4. Use one of the two equations from step 2 to find the value of the parameter |b| ||b = \dfrac{c}{2} = \dfrac{3}{2} = 1.5||

Finish by writing the equation of the logarithmic function: |y = \log_3 \big(1.5(x+2)\big).|

1. Find the value of the parameter |b.|

2. Substitute the points |(x,y)| in the equation.

3. Determine the value of the base |c.|

Find the equation of the logarithmic function with the following characteristics.

• The equation of the asymptote is |x=-1.|

• Its |x|-intercept is |-\dfrac{1}{2}.|

• It goes through the point |(4,1).|

1. Find the value of the parameter |b|
   Given the value of the parameter |h| and the |x|-intercept, the value of parameter |b| can be found. Therefore, ||\begin{align}
   \dfrac{1}{b} + h & = \text{x-intercept} \\\\
   \dfrac{1}{b} -1 &= -\dfrac{1}{2}\\\\
   \dfrac{1}{b} &= \dfrac{1}{2} \\\\
   b &=2 \end{align}||

2. Substitute the points |(x,y)| in the equation
   Since the curve passes through |(4,1),| the result is the following. ||\begin{align}
   y & = \log_c \big(2(x+1)\big) \\
   1 &= \log_c \big(2(4+1)\big)\end{align}||

3. Find the value of the base |c|
   According to the equation obtained previously, ||\begin{align}
   1&= \log_c \big(2(4+1)\big) \\
   c^1 &= 2(4+1)\\
   c^1 &= 10 \\
   c & = 10\end{align}||

Answer: The equation of the function is |y= \log_{10} \big(2(x+1)\big).|