Subjects
Grades
In some situations, it is useful to switch from a percentage to a fraction or vice versa. The following concept sheet outlines the methods used to perform these conversions.
It is possible to express a fraction as a percentage. Here are two methods that can be used.
The following method is most efficient when the denominator of the starting fraction is a divisor or multiple of |100|. Simply find an equivalent fraction whose denominator is |100.|
Determine the number by which to multiply or divide the denominator to obtain |100.|
Multiply or divide the numerator and denominator of the fraction by this number.
Write the numerator of the fraction obtained in step 2 and add the % symbol to the right of it.
Express the fraction |\displaystyle \frac{6}{25}| as a percentage.
Determine the number by which to multiply or divide the denominator to obtain |100|
It is possible to multiply the denominator of the fraction by |\color{green}{4}| to obtain |100|.||25\times \color{green}{4}=100||
Multiply or divide the numerator and denominator of the fraction by this number.||\displaystyle \frac{6\times \color{green}{4}}{25\times \color{green}{4}}=\frac{24}{100}||
Write the numerator of the fraction obtained in step 2 and add the % symbol to the right of it
The answer is then |24\ \%.|
The following example uses division instead of multiplication to obtain a denominator of |100.|
Express the fraction |\dfrac{163}{200}| as a percentage.
Determine the number by which to multiply or divide the denominator to obtain |100|
It is possible to divide the denominator of the fraction by |\color{green}{2}| to obtain |100|.||200\div \color{green}{2}=100||
Multiply or divide the numerator and denominator of the fraction by this number ||\displaystyle \frac{163\div \color{green}{2}}{200\div \color{green}{2}}=\frac{81{.}5}{100}||
Write the numerator of the fraction obtained in step 2 and add the % symbol to the right of it
The answer is then |81{.}5\ \%.|
This method is a little more complex than the first one but more versatile.
Divide the numerator by the denominator.
Multiply the quotient by |100.|
Add the % symbol to the right of the result.
Write the fraction |\dfrac{5}{8}| as a percentage.
Divide the numerator by the denominator
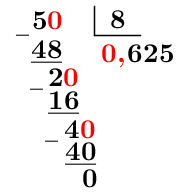
Multiply the quotient by |100| ||0{.}625\times 100=62{.}5||
Add the % symbol to the right of the result
|\dfrac{5}{8}| equals |62{.}5\ \%.|
Just as a percentage can be expressed as a fraction whose denominator is |100|, it is possible to convert a percentage to a fraction using the following method.
Express the percentage as a fraction whose denominator is |100.|
If the numerator is not a whole number, convert it into a whole number by multiplying the numerator and the denominator by an appropriate power of |10|.
|
Number of digits after the decimal |
Power of |10| |
|
|1| |
|10| |
|
|2| |
|100| |
|
|3| |
|1\ 000| |
|
... |
... |
If necessary, simplify the fraction to obtain an irreducible fraction.
There are two possible situations: either the percentage is a whole number, or the percentage is not a whole number. Here is an example of each situation.
Express |28\ \%| in the form of an irreducible fraction.
Express the percentage as a fraction whose denominator is |100|||\dfrac{28}{100}||
If the numerator is not a whole number, convert it into a whole number by multiplying the numerator and the denominator by an appropriate power of |10|
Since the numerator is a whole number, we can go directly to step 3.
If necessary, simplify the fraction to obtain an irreducible fraction ||\dfrac{28\color{green}{\div 4}}{100\color{green}{\div 4}}=\dfrac{7}{25}||
|28\ \%| is equivalent to the irreducible fraction |\dfrac{7}{25}.|
Here is an example where the numerator is not a whole number.
Express |72{.}4\ \%| in the form of an irreducible fraction.
Express the percentage as a fraction whose denominator is |100| ||72{.}4\ \%=\displaystyle \frac{72{.}4}{100}||
If the numerator is not a whole number, convert it into a whole number by multiplying the numerator and the denominator by an appropriate power of |10|
Since the numerator has a number after the decimal point, we will have to multiply the numerator and the denominator by |10.| ||\dfrac{72{.}4\color{green}{\times 10}}{100\color{green}{\times 10}}=\dfrac{724}{1\ 000}||
If necessary, simplify the fraction to obtain an irreducible fraction
Simplify the fraction.||\dfrac{724\color{green}{\div 4}}{1\ 000\color{green}{\div 4}}=\dfrac{181}{250}||
|72{.}4\ \%| is equivalent to the irreducible fraction |\dfrac{181}{250}.|