Subjects
Grades
Metric Relations in a Right Triangle
Concept sheet | Mathematics
Secondary
4-5
In a right triangle, if the height |(\boldsymbol{h})| is drawn from the right angle, 2 new right triangles are created. We can prove that these 3 triangles are similar to each other using the minimum condition A-A.
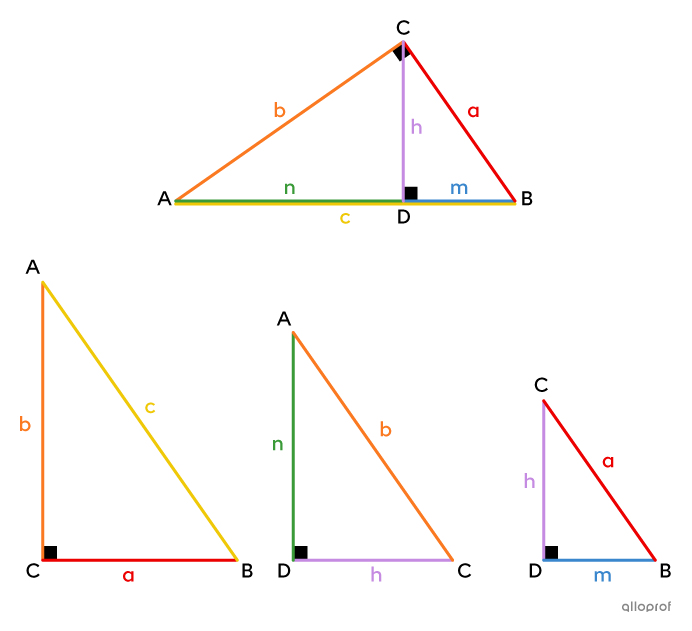
It is possible to create several proportions from the corresponding sides of these right triangles. These proportions yield 3 metric relations that can be used to find missing measurements in right triangles.
||\begin{align}\dfrac{\color{#3b87cd}m}{\color{#ec0000}a}&=\dfrac{\color{#EC0000}a}{\color{#efc807}c}\\\\
\dfrac{\color{#3a9a38}n}{\color{#fa7921}b}&=\dfrac{\color{#fa7921}b}{\color{#efc807}c}\end{align}||
Altitude to Hypotenuse Theorem
||\dfrac{\color{#3b87cd}m}{\color{#c58ae1}h}=\dfrac{\color{#c58ae1}h}{\color{#3a9a38}n}||
||\dfrac{\color{#c58ae1}h}{\color{#ec0000}a}=\dfrac{\color{#fa7921}b}{\color{#efc807}c}||
Here are the steps to find the length of a segment in a triangle using metric relations.
-
Identify the given measurements and the unknown measurement.
-
Determine which metric relation to use.
-
Find the missing measurement.
If more than one measure is missing in order for a metric relation to be used, one can sometimes be found using the Pythagorean theorem.
Proportional Mean Theorem
In a right triangle, each leg |(a| and |b)| is the proportional mean between its projection onto the hypotenuse |(m| or |n)| and the entire hypotenuse |(c).|
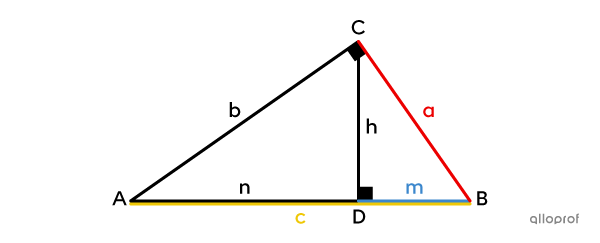
|\dfrac{\color{#3b87cd}m}{\color{#ec0000}a}=\dfrac{\color{#ec0000}a}{\color{#efc807}c}\ \Rightarrow\ \color{#ec0000}a^2= \color{#3b87cd}m\color{#efc807}c|
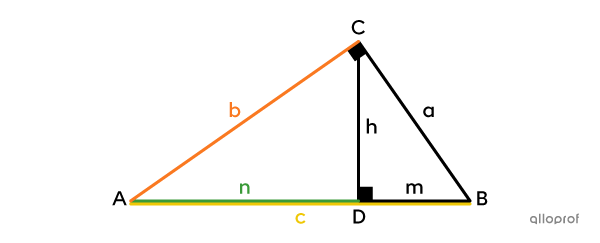
|\dfrac{\color{#3a9a38}n}{\color{#fa7921}b}=\dfrac{\color{#fa7921}b}{\color{#efc807}c}\ \Rightarrow\ \color{#fa7921}b^2=\color{#3a9a38}n\color{#efc807}c|
Determine the measure of |\overline{BC}| in the following triangle.
-
Identify the given measurements and the unknown measurement.
||\begin{align}\text{m}\overline{AB}&=c=16\ \text{cm}\\\text{m}\overline{BD}&=m=4\ \text{cm}\\\text{m}\overline{BC}&=a=\ ?\end{align}|| -
Determine which metric relation to use.
We are looking for the metric relation that involves measurements |a,| |c| and |m.| This is the Proportional Mean theorem. -
Find the missing measurement.
||\begin{align}a^2 &= m c \\a^2 &= 4\times 16\\a^2 &= 64\\a &= 8\end{align}||
Answer: Segment |\overline{BC}| measures |8\ \text{cm}.|
Altitude to Hypotenuse Theorem
In a right triangle, the height |(h)| drawn from the right angle is the proportional mean between the 2 segments it creates on the hypotenuse |(m| and |n).|
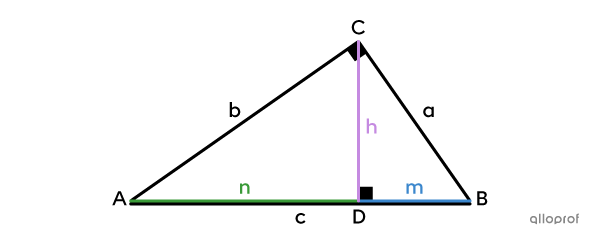
|\dfrac{\color{#3b87cd}m}{\color{#c58ae1}h}=\dfrac{\color{#c58ae1}h}{\color{#3a9a38}n}\ \Rightarrow\ \color{#c58ae1}h^2 = \color{#3b87cd}m\color{#3a9a38}n|
Find the measure of |\overline{BD}| in the following triangle.
-
Identify the given measurements and the unknown measurement.
||\begin{align}\text{m}\overline{AD}&=n=12\ \text{cm}\\
\text{m}\overline{CD}&=h=6\ \text{cm}\\
\text{m}\overline{BD}&=m=\ ?\end{align}|| -
Determine which metric relation to use.
We are looking for the metric relation that involves measurements |h,| |m| and |n.| This is the Altitude to Hypotenuse theorem. -
Find the missing measurement.
||\begin{align}h^2 &= mn\\6^2 &= 12\times m\\36 &= 12\times m\\3 &= m\end{align}||
Answer: Segment |\overline{BD}| measures |3\ \text{cm}.|
Product of the Sides Theorem
In a right triangle, the product of hypotenuse |(c)| and the corresponding height |(h)| is equal to the product of the legs |(a| and |b).|
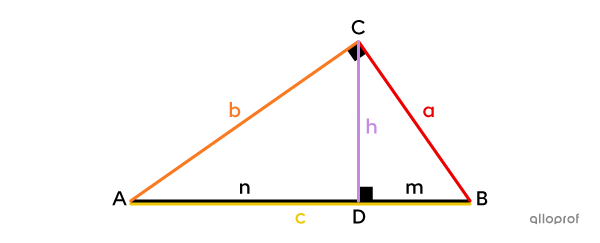
|\dfrac{\color{#c58ae1}h}{\color{#ec0000}a}=\dfrac{\color{#fa7921}b}{\color{#efc807}c}\ \Rightarrow\ \color{#efc807}c\color{#c58ae1}h = \color{#ec0000}a\color{#fa7921}b|
Find the measure of |\overline{CD}| in the following triangle.
-
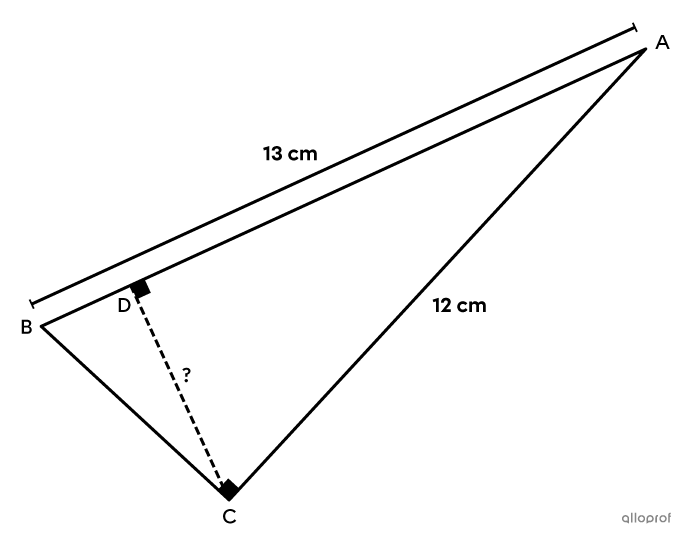
Identify the given measurements and the unknown measurement.
||\begin{align}\text{m}\overline{AB}&=c=13\ \text{cm}\\
\text{m}\overline{AC}&=b=12\ \text{cm}\\
\text{m}\overline{CD}&=h=\ ?\end{align}|| -
Determine which metric relation to use.No metric relation uses only these 3 values. However, if we use the Product of the Sides theorem, only the length of the second leg is missing |(\overline{BC}),| and it can be found using the Pythagorean theorem.||\begin{align} a^2 + b^2 &= c^2\\a^2 + 12^2 &= 13^2\\a^2 &= 169 - 144\\a^2 &= 25\\a &= 5\end{align}||
-
Find the missing measurement.
||\begin{align}ch&=ab\\13h &= 5\times 12\\13h &= 60\\h &\approx 4.6\end{align}||
Answer: Segment |\overline{CD}| measures approximately |4.6\ \text{cm}.|
Solving Problems Involving Metric Relations
More complex problems can be solved by using multiple metric relations.
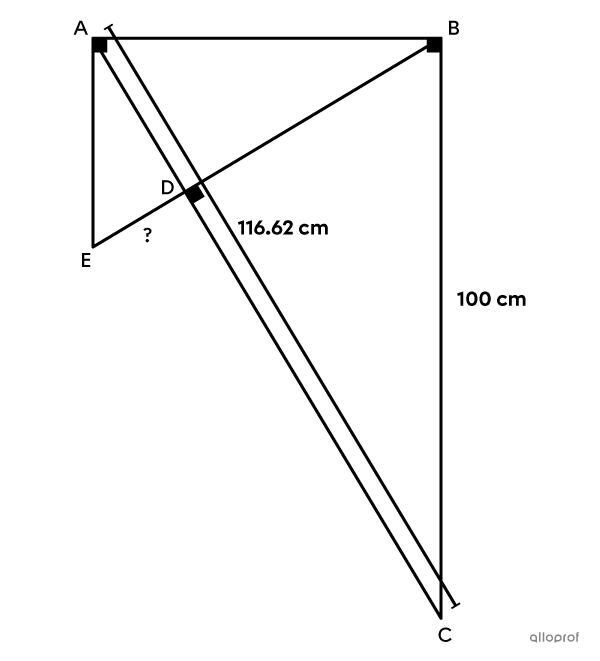
In the image below, segment |\overline{BC}| measures |100\ \text{cm},| and segment |\overline{AC}| measures |116.62\ \text{cm}.| Find the length of segment |\overline{DE}.|
