In the following animation, experiment with modifying the parameters |a,| |h,| and |k| of the quadratic (or second-degree polynomial) function. Observe the effects of the parameters on the function’s properties. Afterwards, consult the concept sheet for all of the details concerning the properties of the function.

Properties of Quadratic Functions in the Form |f(x)=ax^2|

Properties	Quadratic function in the form \|\|f(x)=ax^2\quad \text{where}\quad a<0\|\|The curve of the function opens downwards.	Quadratic function in the form \|\|f(x)=ax^2\quad \text{where}\quad a>0\|\|The curve of the function opens upwards.
Domain	The set of real numbers \|\mathbb{R}\|	The set of real numbers \|\mathbb{R}\|
Range (image)	The set of negative real numbers, \|\mathbb{R}_-\|.	The set of positive real numbers, \|\mathbb{R}_+\|.
\|y\|-Intercept	\|0\|	\|0\|
\|x\|-intercept (zeroes of the function)	\|0\|	\|0\|
Vertex	The point \|(0,0)\|	The point \|(0,0)\|
Variation or increasing and decreasing intervals	The function increases over \|]\text{-}\infty, 0]\| and decreases over \|[0,\infty[.\|	The function increases over \|[0,\infty[\| and decreases over \|]\text{-}\infty,0].\|
Extrema	The function has a maximum of \|y=0.\|	The function has a minimum of \|y=0.\|
Signs or positive and negative intervals	The function is negative over all its domain.	The function is positive over all its domain.
Axis of symmetry	The equation of the axis of symmetry is \|x=0.\|	The equation of the axis of symmetry is \|x=0.\|

Properties of a Quadratic Function in General Form, Standard Form, and Factored Form

Properties	General form \|f(x)=ax^2+bx+c\|	Standard form \|f(x)=a(x-h)^2+k\|	Factored form \|f(x)=a(x-x_1)(x-x_2)\|
Domain	\|x \in \mathbb{R}\|
Range	If \|a>0\|, then \|\left[\frac{4ac-b^2}{4a}, +\infty \right[.\| If \|a<0\|, then \|\left]-\infty, \frac{4ac-b^2}{4a}\right].\|	If \|a>0\|, then \|[k,+\infty[.\| If \|a<0\|, then \|]-\infty, k].\|	If \|a>0\|, then \|\left[\frac{-a(x_2-x_1)^2}{4},+\infty\right[.\| If \|a<0\|, then \|\left] - \infty, \frac{-a(x_2-x_1)^2}{4} \right].\|
\|y\|-intercept \|\big(f(0)\big)\|	\|f(0)=c\|	\|f(0)=ah^2+k\|	\|f(0)=ax_1x_2\|
\|y\|-intercept \|\big(f(0)\big)\|	Replace \|x\| with \|0\| in the equation and calculate the value of \|y.\|
\|x\|-intercept (zeroes of the function)	If \|b^2-4ac>0\|, then there are 2 distinct zeroes. If \|b^2-4ac=0\|, then there is only one zero. If \|b^2-4ac<0\|, then there is no zero. Zeroes can be found by factorization or the quadratic formula. \|\|x_{1,2}=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\|\|	If \|a\| and \|k\| have different signs, then there will be 2 distinct zeroes. If \|k=0\|, then there will be a single zero. If \|a\| and \|k\| have the same sign, then there will be no zero. Zeroes can be found by replacing \|f(x)\| by \|0\| and isolating \|x\|, or by using the following formula. \|\|x_{1,2}=h\pm \sqrt{\frac{-k}{a}}\|\|	The zeroes are \|x_1\| and \|x_2.\|
Vertex	\|\left(\dfrac{-b}{2a},\dfrac{4ac-b^2}{4a}\right)\|	\|(h,k)\|	\|\left(\dfrac{x_1+x_2}{2},\dfrac{-a(x_2-x_1)^2}{4}\right)\|
Variation or Increasing and decreasing intervals	If \|a>0\|, then the function decreases over \|\left]-\infty,\frac{-b}{2a}\right]\| and increases over \|\left[\frac{-b}{2a},+\infty\right[.\| If \|a<0\|, then the function increases over \|\left]-\infty,\frac{-b}{2a}\right]\| and decreases over \|\left[\frac{-b}{2a},+\infty\right[.\|	If \|a>0\|, then the function decreases over \|]-\infty,h]\| and increases over \|[h,+\infty[.\| If \|a<0\|, then the function increases over \|]-\infty,h]\| and decreases over \|[h,+\infty[.\|	If \|a>0\|, then the function decreases over \|\left]-\infty,\frac{x_1+x_2}{2}\right]\| and increases over \|\left[\frac{x_1+x_2}{2},+\infty\right[.\| If \|a<0\|, then the function increases over \|\left]-\infty,\frac{x_1+x_2}{2}\right]\| and decreases over \|\left[\frac{x_1+x_2}{2},+\infty\right[.\|
Extrema	\|\dfrac{4ac-b^2}{4a}\| A maximum if \|a<0.\| A minimum if \|a>0.\|	\|k\| A maximum if \|a<0.\| A minimum if \|a>0.\|	\|\dfrac{-a(x_2-x_1)^2}{4}\| A maximum if \|a<0.\| A minimum if \|a>0.\|
Signs or Positive and negative intervals	If \|a>0\| and there is only one or no zero, then the function is positive for all \|x.\| If \|a<0\| and there is only one or no zero, then the function is negative for all \|x.\| If \|a>0\| and there are 2 zeroes, then the function is negative for the interval between the 2 zeroes and positive for all other \|x.\| If \|a<0\| and there are 2 zeroes, then the function is positive for the interval between the 2 zeroes and negative for all other \|x.\|
Axis of symmetry	\|x=\dfrac{-b}{2a}\|	\|x=h\|	\|x=\dfrac{x_1+x_2}{2}\|
Asymptotes	There are no asymptotes.

Example

Determine the properties of the quadratic function with the following equation. ||f(x)=-2x^2-x+3||

It may be useful to sketch the graph of the function.

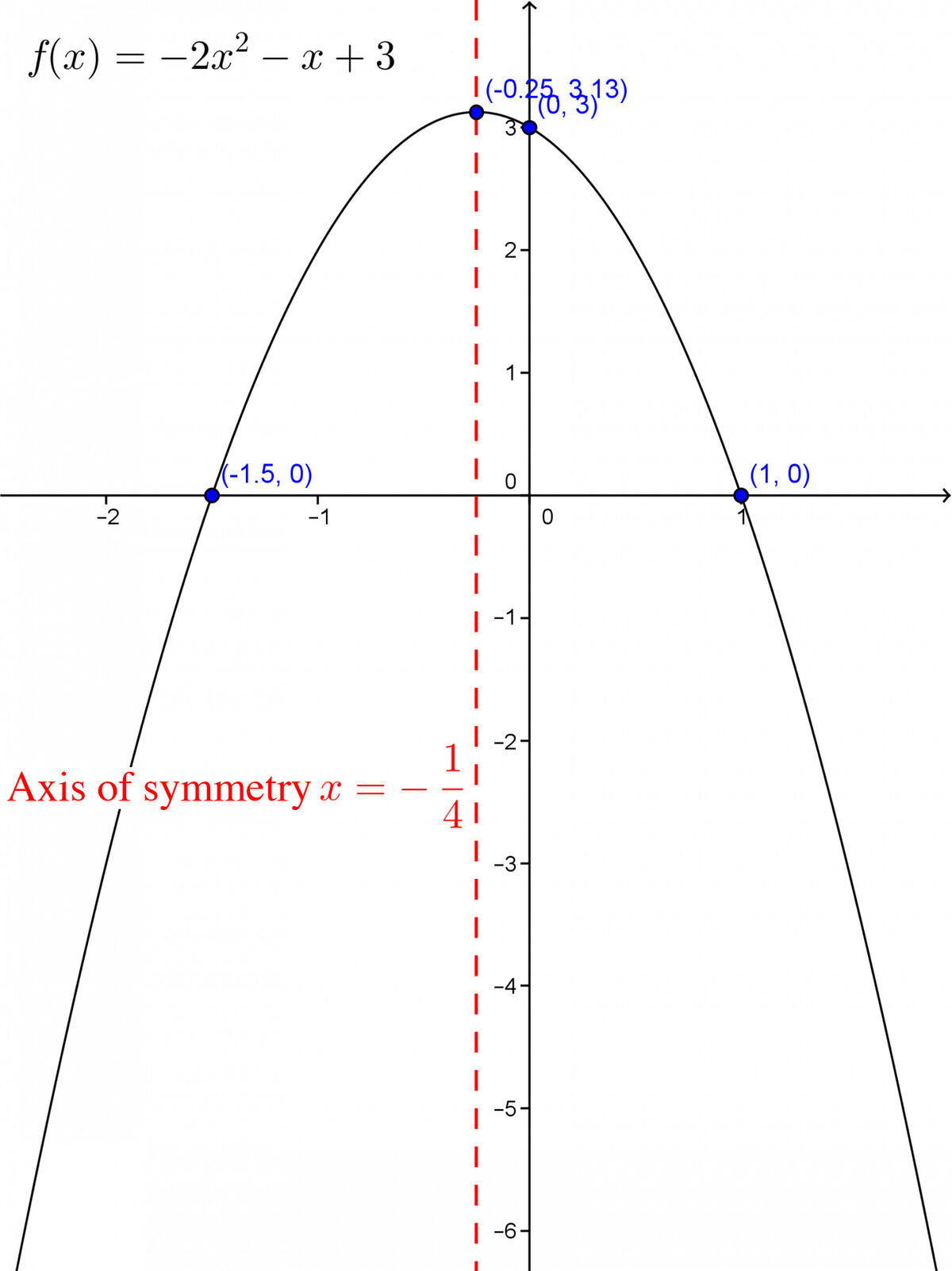
Graph illustrating a parabola opening downwards

The domain of the function is |\mathbb{R}.|
To determine the range of the function, it is important to know if the function opens upwards or downwards, as well as the |y|-coordinate of the vertex, i.e. the parameter |k.|
The parameter |a| is negative, so the graph of the function must open downwards (the graph confirms it). As for the parameter |k,| it must be calculated using the formula |\displaystyle k=\frac{4ac-b^2}{4a}.| ||\begin{align} k &= \frac{4ac-b^2}{4a} \\ &= \frac{4(-2)(3) - (-1)^2}{4 (-2)} \\ &= \frac{-25}{-8} \\ &= \frac{25}{8} \end{align}||Thus, the range of the function is |]-\infty, \frac{25}{8}].|
The |y|-intercept of a quadratic polynomial function in general form is given by the value of |c|, which here is |3.|
The zeroes of the function can be found using the quadratic formula. ||\begin{align} x_{1,2} &= \frac{-b \pm\sqrt{b^2-4ac}}{2a} \\ &= \frac{-(-1) \pm \sqrt{(-1)^2-4 (-2) (3)}}{2 (-2)} \\ &= \frac{1 \pm \sqrt{25}}{-4} \end{align}||Next, separate the formula into two answers: one using the |+| and the other using the |-.| |x_1| will be one zero and |x_2| will be the other zero. ||\begin{align} x_1 &= \frac{1+\sqrt{25}}{-4} = \frac{1+5}{-4}=\frac{6}{-4}=- \frac{3}{2} \\ x_2 &= \frac{1-\sqrt{25}}{-4}=\frac{1-5}{-4}=\frac{-4}{-4}=1 \end{align}||Thus, the two zeroes of the function are |-\dfrac{3}{2}| and |1.|
To find the parameter |h,| calculate the average between the two zeroes. ||h = \frac{-\frac{3}{2}+1}{2} = \frac{-\frac{1}{2}}{2}=-\frac{1}{4}||Thus, the coordinates of the vertex are |\displaystyle (h,k)=\left( -\frac{1}{4}, \frac{25}{8} \right).|
The variation or intervals of increase and decrease: the function increases over |\left]-\infty, -\dfrac{1}{4}\right]| and decreases over |\left[-\dfrac{1}{4}, +\infty\right[.|
Extrema: because the graph of the function opens downwards, it has a maximum of |y=k,| i.e. the maximum is |\dfrac{25}{8}.|
The sign or the positive and negative intervals: the function is positive over |[-1.5, 1]| and negative over |]-\infty, -1.5] \cup [1, +\infty[.|
The equation of the axis of symmetry is |x=h.| Therefore, |x= -\dfrac{1}{4}.|

To determine the properties of a quadratic function, it is easiest to work with the standard form of the function.

Example

Determine the properties of the quadratic function with the following equation. ||f(x)=2(x-2)^2+5||

It may be useful to sketch a graph of the function.

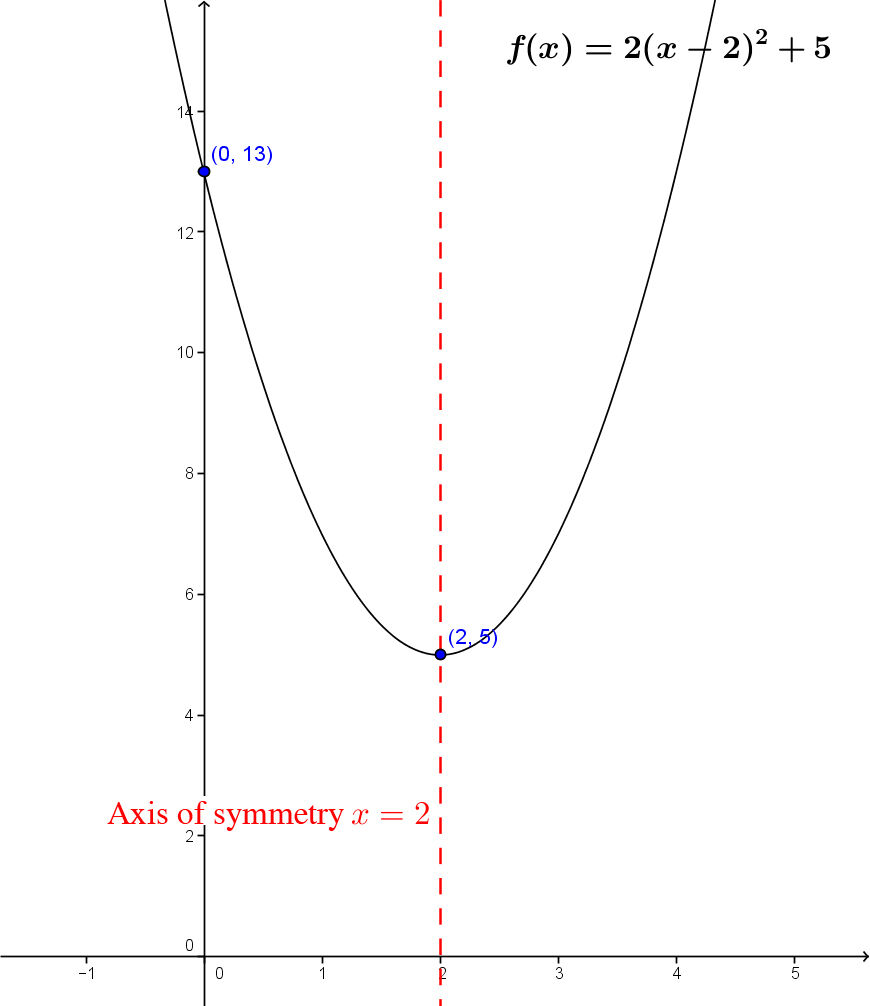
The domain of the function is |\mathbb{R}.|
The function’s range is |[5, +\infty[.| The function opens upwards, because its parameter |a| is positive and the |y|-coordinate of the vertex is |5.|
The |y|-intercept of a quadratic function in standard form is calculated by replacing |x| with |0.|||\begin{align} f(x) &= 2(x-2)^2+5 \\ f(0) &= 2(0-2)^2+5 \\ f(0) &= 2(-2)^2+5 \\ f(0) &= 2 (4) + 5 \\ f(0) &= 8 + 5 \\ f(0) &= 13 \end{align}|| The |y|-intercept of the function is |13.|
Since the |y|-coordinate of the vertex is greater than |0| and the graph of the function opens upwards, the function does not have a zero.
The coordinates of the vertex are |(h,k)=(2,5).|
The function increases over |[2, +\infty[| and decreases over |]-\infty,2].|
Since the graph of the function is open upwards, it has a minimum when |y=k|, i.e. the minimum is |5.|
As the range of the function is always positive |([5, + \infty[),| the function is positive over its entire domain.
The equation of the axis of symmetry is |x=h.| Thus, |x=2.|

Exercises

Exercise

Properties	Quadratic function in the form \|\|f(x)=ax^2\quad \text{where}\quad a<0\|\|The curve of the function opens downwards.	Quadratic function in the form \|\|f(x)=ax^2\quad \text{where}\quad a>0\|\|The curve of the function opens upwards.
Domain	The set of real numbers \|\mathbb{R}\|	The set of real numbers \|\mathbb{R}\|
Range (image)	The set of negative real numbers, \|\mathbb{R}_-\|.	The set of positive real numbers, \|\mathbb{R}_+\|.
\|y\|-Intercept	\|0\|	\|0\|
\|x\|-intercept (zeroes of the function)	\|0\|	\|0\|
Vertex	The point \|(0,0)\|	The point \|(0,0)\|
Variation or increasing and decreasing intervals	The function increases over \|]\text{-}\infty, 0]\| and decreases over \|[0,\infty[.\|	The function increases over \|[0,\infty[\| and decreases over \|]\text{-}\infty,0].\|
Extrema	The function has a maximum of \|y=0.\|	The function has a minimum of \|y=0.\|
Signs or positive and negative intervals	The function is negative over all its domain.	The function is positive over all its domain.
Axis of symmetry	The equation of the axis of symmetry is \|x=0.\|	The equation of the axis of symmetry is \|x=0.\|

Properties	General form \|f(x)=ax^2+bx+c\|	Standard form \|f(x)=a(x-h)^2+k\|	Factored form \|f(x)=a(x-x_1)(x-x_2)\|
Domain	\|x \in \mathbb{R}\|
Range	If \|a>0\|, then \|\left[\frac{4ac-b^2}{4a}, +\infty \right[.\| If \|a<0\|, then \|\left]-\infty, \frac{4ac-b^2}{4a}\right].\|	If \|a>0\|, then \|[k,+\infty[.\| If \|a<0\|, then \|]-\infty, k].\|	If \|a>0\|, then \|\left[\frac{-a(x_2-x_1)^2}{4},+\infty\right[.\| If \|a<0\|, then \|\left] - \infty, \frac{-a(x_2-x_1)^2}{4} \right].\|
\|y\|-intercept \|\big(f(0)\big)\|	\|f(0)=c\|	\|f(0)=ah^2+k\|	\|f(0)=ax_1x_2\|
\|y\|-intercept \|\big(f(0)\big)\|	Replace \|x\| with \|0\| in the equation and calculate the value of \|y.\|
\|x\|-intercept (zeroes of the function)	If \|b^2-4ac>0\|, then there are 2 distinct zeroes. If \|b^2-4ac=0\|, then there is only one zero. If \|b^2-4ac<0\|, then there is no zero. Zeroes can be found by factorization or the quadratic formula. \|\|x_{1,2}=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\|\|	If \|a\| and \|k\| have different signs, then there will be 2 distinct zeroes. If \|k=0\|, then there will be a single zero. If \|a\| and \|k\| have the same sign, then there will be no zero. Zeroes can be found by replacing \|f(x)\| by \|0\| and isolating \|x\|, or by using the following formula. \|\|x_{1,2}=h\pm \sqrt{\frac{-k}{a}}\|\|	The zeroes are \|x_1\| and \|x_2.\|
Vertex	\|\left(\dfrac{-b}{2a},\dfrac{4ac-b^2}{4a}\right)\|	\|(h,k)\|	\|\left(\dfrac{x_1+x_2}{2},\dfrac{-a(x_2-x_1)^2}{4}\right)\|
Variation or Increasing and decreasing intervals	If \|a>0\|, then the function decreases over \|\left]-\infty,\frac{-b}{2a}\right]\| and increases over \|\left[\frac{-b}{2a},+\infty\right[.\| If \|a<0\|, then the function increases over \|\left]-\infty,\frac{-b}{2a}\right]\| and decreases over \|\left[\frac{-b}{2a},+\infty\right[.\|	If \|a>0\|, then the function decreases over \|]-\infty,h]\| and increases over \|[h,+\infty[.\| If \|a<0\|, then the function increases over \|]-\infty,h]\| and decreases over \|[h,+\infty[.\|	If \|a>0\|, then the function decreases over \|\left]-\infty,\frac{x_1+x_2}{2}\right]\| and increases over \|\left[\frac{x_1+x_2}{2},+\infty\right[.\| If \|a<0\|, then the function increases over \|\left]-\infty,\frac{x_1+x_2}{2}\right]\| and decreases over \|\left[\frac{x_1+x_2}{2},+\infty\right[.\|
Extrema	\|\dfrac{4ac-b^2}{4a}\| A maximum if \|a<0.\| A minimum if \|a>0.\|	\|k\| A maximum if \|a<0.\| A minimum if \|a>0.\|	\|\dfrac{-a(x_2-x_1)^2}{4}\| A maximum if \|a<0.\| A minimum if \|a>0.\|
Signs or Positive and negative intervals	If \|a>0\| and there is only one or no zero, then the function is positive for all \|x.\| If \|a<0\| and there is only one or no zero, then the function is negative for all \|x.\| If \|a>0\| and there are 2 zeroes, then the function is negative for the interval between the 2 zeroes and positive for all other \|x.\| If \|a<0\| and there are 2 zeroes, then the function is positive for the interval between the 2 zeroes and negative for all other \|x.\|
Axis of symmetry	\|x=\dfrac{-b}{2a}\|	\|x=h\|	\|x=\dfrac{x_1+x_2}{2}\|
Asymptotes	There are no asymptotes.

The Properties of Quadratic Functions

Properties of Quadratic Functions in the Form |f(x)=ax^2|

Properties of a Quadratic Function in General Form, Standard Form, and Factored Form

See also

Exercises

The Properties of a Quadratic Function

Receive all the info and tips from Alloprof by email.