Subjects
Grades
In mathematics, a proportion is a relation of equality between two ratios or rates.
To form a proportion, the two ratios or rates must be equivalent.
It is important to review the following concepts to fully understand the notion of proportion.
The following ratios are proportional: ||\displaystyle 3:4=15:20||
Thus, the two ratios are equivalent. ||\begin{align}3\div 4&=0.75\\ 15\div20&=0.75\end{align}||
The following rates are proportional: ||\displaystyle \frac{300\ \text{inhabitants}}{5\ \text{km}^2}=\frac{600\ \text{inhabitants}}{10\ \text{km}^2}|| Thus, the two rates are equivalent. ||\begin{align}300\div 5&=60\ \text{inhabitants/km}^2\\ 600\div 10&=60\ \text{inhabitants/km}^2\end{align}||
Since a proportion is the equality between two ratios or rates, there will always be four terms.
In a proportion, the first and fourth terms are called the extremes of the proportion. The second and third terms are called the means of the proportion. ||\displaystyle \frac{\text{Extreme}}{\text{Mean}}=\frac{\text{Mean}}{\text{Extreme}}|| In other words, in the proportion ||\color{blue}{a}:\color{green}{b}=\color{green}{c}:\color{blue}{d}\\ \text{or}\\ \displaystyle \frac{\color{blue}{a}}{\color{green}{b}}=\frac{\color{green}{c}}{\color{blue}{d}}|| terms |\color{blue}{a}| and |\color{blue}{d}| are the extremes and terms |\color{green}{b}| and |\color{green}{c}| are the means.
Consider the following proportion: ||\displaystyle \frac{\color{blue}{1}}{\color{green}{2}}=\frac{\color{green}{4}}{\color{blue}{8}}|| Terms |\color{blue}{1}| and |\color{blue}{8}| are the extremes.
Terms |\color{green}{2}| and |\color{green}{4}| are the means.
The following section presents the fundamental property of proportions.
In a proportion, the product of the extremes is equal to the product of the means.
If |\displaystyle \frac{\color{blue}{a}}{\color{green}{b}}=\frac{\color{green}{c}}{\color{blue}{d}}|,
thus |\color{blue}{a}\times \color{blue}{d}=\color{green}{b}\times \color{green}{c}|.
Consider the following proportion: ||\displaystyle \frac{3}{4}=\frac{9}{12}|| Note the product of the extremes is equal to the product of the means. ||\begin{align}3\times 12&=4\times 9\phantom{1}\\36&=36\end{align}||
This property results in cross multiplication which makes it possible to find a missing term in a proportion – the same cross multiplication that can be used to solve a proportional situation.
The proportionality ratio is the number by which to multiply the numerator of a proportion’s rates or ratios to obtain the denominator.
Consider the following proportion: ||\displaystyle \frac{2}{6}=\frac{7}{21}|| In this proportion, the proportionality ratio is |\color{red}{3}|.
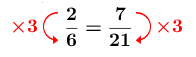
The proportionality ratio can be used to solve a proportional situation.
In a proportion, the factor of change is the number by which to multiply the numerator (or denominator) of one ratio or rate to obtain the numerator (or denominator) of the other ratio or rate.
Consider the following proportion: ||\displaystyle \frac{4}{5}=\frac{24}{30}||
In this proportion, the factor of change is |\color{red}{6}|.
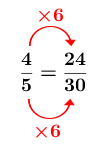
The factor of change can also be used to solve a proportional situation.