Subjects
Grades
Proving Vector Statements
Concept sheet | Mathematics
Secondary
5
Table of contents
- Top of page
- Prove that if |\overrightarrow{u} = (a,b)|, then |\mid \mid \overrightarrow{u}\mid \mid =\mid \mid -\overrightarrow{u}\mid \mid |.
- Prove that |\overrightarrow{u} \cdot \overrightarrow{u} =\mid \mid \overrightarrow{u}\mid \mid ^{2}|.
- Show that the diagonals of a rhombus are perpendicular
- If |ABCD| is a parallelogram, then the diagonals intersect at their midpoints.
- Show that the line segment that connects the midpoints of two sides of a triangle is parallel to the 3rd side and equal to half of the 3rd side’s length.
There is no single procedure to prove statements using vectors.
- Prove that if |\overrightarrow{u} = (a,b)|, then |\mid \mid \overrightarrow{u} \mid \mid = \mid \mid - \overrightarrow{u}\mid\mid|
- Prove that |\overrightarrow{u} \cdot \overrightarrow{u}=\mid \mid \overrightarrow{u}\mid \mid ^{2}|
- Show that the diagonals of a rhombus are perpendicular
- If |ABCD| is a parallelogram, then the diagonals intersect at their midpoints
- Prove that the line segment that connects the midpoints of two sides of a triangle is parallel to the 3rd side and equal to half of the 3rd side’s length
However, some strategies can be effective for proving these statements.
-
Set up a plan for proving the statement (mentally or on paper) before starting the calculations.
-
Work in a structured way. Tables like the ones used in the examples below often make a proof clearer.
-
Make use of Chasles' relation.
Prove that if |\overrightarrow{u} = (a,b)|, then |\mid \mid \overrightarrow{u}\mid \mid =\mid \mid -\overrightarrow{u}\mid \mid |.
|
Statement |
Justification |
|---|---|
|
|\mid \mid \overrightarrow{u}\mid \mid =\sqrt{a^{2}+b^{2}}| |
By definition |
|
|-\overrightarrow{u}=(-a,-b)| |
Opposite vector |
|
|\mid \mid - \overrightarrow{u}\mid \mid =\sqrt{(-a)^{2}+(-b)^{2}}| |
By definition |
|
|\mid \mid -\overrightarrow{u}\mid \mid =\sqrt{a^{2}+b^{2}}| |
By calculation |
|
The right sides of statements 1 and 4 are the same. |
Observation |
|
|\mid \mid \overrightarrow{u}\mid \mid =\mid \mid -\overrightarrow{u}\mid \mid | |
By the transitive property |
Prove that |\overrightarrow{u} \cdot \overrightarrow{u} =\mid \mid \overrightarrow{u}\mid \mid ^{2}|.
Let |\overrightarrow{u}=(r,s)|.
|
Statement |
Justification |
|---|---|
|
|\overrightarrow{u} \cdot \overrightarrow{u}=ac+bd| |
Definition of the dot product |
|
|\overrightarrow{u} \cdot \overrightarrow{u} =r^{2}+s^{2}| |
Substituting in the correct components |
|
|\mid \mid \overrightarrow{u}\mid \mid ^{2}=(\sqrt{a^{2}+b^{2}})^{2}| |
By definition |
|
|\mid \mid \overrightarrow{u}\mid \mid ^{2}=(\sqrt{r^{2}+s^{2}})^{2}| |
Substituting in the correct components |
|
|\mid \mid \overrightarrow{u}\mid \mid ^{2}=r^{2}+s^{2}| |
By calculation |
|
The right sides of statements 3 and 6 are the same. |
Observation |
|
|\overrightarrow{u} \cdot \overrightarrow{u}=\mid \mid \overrightarrow{u}\mid \mid ^{2}| |
By the transitive property |
Show that the diagonals of a rhombus are perpendicular
Hypothesis: |ABCD| is a rhombus.
Conclusion: |\overrightarrow{AC}\perp\overrightarrow{BD}|
So, we need to show that |\overrightarrow{AC}\cdot\overrightarrow{BD}=0| (dot product).
|
Affirmations |
Justifications |
|---|---|
|
|\overrightarrow{AC}\cdot\overrightarrow{BD}=(\overrightarrow{AB}+\overrightarrow{BC})\cdot(\overrightarrow{BA}+\overrightarrow{AD})| |
By Chasles’ relation |
|
|\overrightarrow{AC}\cdot\overrightarrow{BD}=(\overrightarrow{AB}+\overrightarrow{AD})\cdot(\overrightarrow{BA}+\overrightarrow{AD})| |
These are congruent sides of the rhombus |
|
|\overrightarrow{AC}\cdot\overrightarrow{BD}=(\overrightarrow{AD}+\overrightarrow{AB})\cdot(\overrightarrow{AD}+\overrightarrow{BA})| |
By the commutative property |
|
|\overrightarrow{AC}\cdot\overrightarrow{BD}=(\overrightarrow{AD}+\overrightarrow{AB})\cdot(\overrightarrow{AD}-\overrightarrow{AB})| |
Opposite vector |
|
|\overrightarrow{AC}\cdot\overrightarrow{BD}=\overrightarrow{AD}^2-\overrightarrow{AB}^2| |
Difference of squares |
|
|\overrightarrow{AC}\cdot\overrightarrow{BD}=\mid \mid \overrightarrow{AD}\mid \mid ^{2}-\mid \mid \overrightarrow{AB}\mid \mid ^{2}| |
|\overrightarrow{u}^{2}=\mid \mid \overrightarrow{u}\mid \mid ^{2}| |
|
|\overrightarrow{AC}\cdot\overrightarrow{BD}=\mid \mid \overrightarrow{AB}\mid \mid ^{2}-\mid \mid \overrightarrow{AB}\mid \mid ^{2}| |
Congruent sides of the rhombus |
|
|\overrightarrow{AC}\cdot\overrightarrow{BD}=0| |
By subtraction |
If |ABCD| is a parallelogram, then the diagonals intersect at their midpoints.
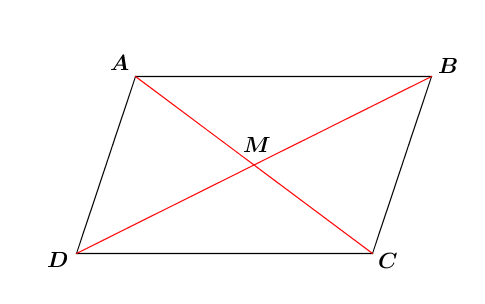
Hypotheses: |ABCD| is a parallelogram and |M| is the midpoint of the diagonal |AC|.
Conclusion: |M| is the midpoint of the diagonal |DB|.
So, we need to show that |\overrightarrow{MB}=\overrightarrow{DM}|.
|
Statement |
Justification |
|---|---|
|
|\overrightarrow{DM}=\overrightarrow{DA}+\overrightarrow{AM}| |
Chasles’ relation |
|
|\overrightarrow{DM}=\overrightarrow{CB}+\overrightarrow{AM}| |
Opposite sides of a parallelogram |
|
|\overrightarrow{DM}=\overrightarrow{CB}+\overrightarrow{MC}| |
By the hypothesis |
|
|\overrightarrow{DM}=\overrightarrow{MC}+\overrightarrow{CB}| |
Commutative property of addition |
|
|\overrightarrow{DM}=\overrightarrow{MB}| |
Chasles’ relation |
Show that the line segment that connects the midpoints of two sides of a triangle is parallel to the 3rd side and equal to half of the 3rd side’s length.
Hypotheses: |ABC| is a triangle and |\overrightarrow{AM}=\overrightarrow{MB}|, so |\overrightarrow{BN}=\overrightarrow{NC}|.
Conclusion: |\displaystyle \overrightarrow{MN}=\frac{1}{2} \overrightarrow{AC}|
|
Statement |
Justification |
|---|---|
|
|\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{BC}| |
Chasles’ relation |
|
|\overrightarrow{AC}=(\overrightarrow{AM}+\overrightarrow{MB})+(\overrightarrow{BN}+\overrightarrow{NC})| |
Chasles’ relation |
|
|\overrightarrow{AC}=\overrightarrow{MB}+\overrightarrow{MB}+\overrightarrow{BN}+\overrightarrow{BN}| |
By the hypothesis |
|
|\overrightarrow{AC}=2\overrightarrow{MB}+2\overrightarrow{BN}| |
Vector addition |
|
|\overrightarrow{AC}=2(\overrightarrow{MB}+\overrightarrow{BN})| |
Common factor |
|
|\overrightarrow{AC}=2\overrightarrow{MN}| |
Chasles’ relation |
|
|\displaystyle \frac{1}{2} \overrightarrow{AC} = \overrightarrow{MN}| |
Divide by 2 |