Subjects
Grades
Two parameters are present in the linear function: the parameter |a,| called the rate of change or slope, and the parameter |b,| called the |y|-intercept or the initial value.
The equation of a linear function is represented by:
||f(x) = \color{red}{a}x + \color{blue}{b}||
where |\color{red}{a}| and |\color{blue}{b}| are real numbers.
In a relationship between two variables, the rate of change (usually represented by the letter |a|) is the relationship between two corresponding changes of the variables.
When two values are related, a change in the values of the independent variable leads to a change in the corresponding values of the dependent variable. It is then possible to define the rate of change as follows.
||\text{Rate of change} = \dfrac{\text{Change in the dependent variable}}{\text{Change in the independent variable}}||
It can be simplified by the following expression.
||a=\dfrac{\Delta y}{\Delta x} = \dfrac{y_2 - y_1}{x_2 - x_1}||
Where |(x_1,y_1)| and |(x_2,y_2)| are two distinct points on the line and |\Delta| is the Greek letter delta representing a change.
In analytical geometry, the rate of change is called the slope of a line.
The |y|-intercept, also called the initial value and denoted |b,| corresponds to the value of the dependent variable |(y)| when the value of the independent variable |(x)| is |0.| Plotted on a graph, the |y|-intercept is the point of intersection between the line and the |y|-axis.
In the following interactive animation, you can modify the value of the parameters |a| and |b| of the linear function using the sliders. It’s also possible to move the two points of the line directly on the graph. Then, you can continue reading the concept sheet to learn how to determine the rate of change |(a)| and the initial value |(b)| from the equation of the line, a table of values, a graph, or a word problem.
The rate of change is denoted by the coefficient of the independent variable |(x).|
The |y|-intercept is the constant term.
In the equation below, the letter |\color{red}{a}| represents the rate of change and the letter |\color{blue}{b}| represents the |y|-intercept. ||y=\color{red}{a}x+\color{blue}{b}||
Examples of equations and their corresponding rate of change.
|
Equation |
Rate of change |
|y|-intercept |
|---|---|---|
|
|y=3x-9| |
|+3| |
|-9| |
|
|y=-8x+2| |
|-8| |
|+2| |
|
|y=4+9x| |
|+9| |
|+4| |
|
|y=\frac{1}{2} - \frac{3}{4}x| |
|- \frac{3}{4}| |
|+\frac{1}{2}| |
|
|y=x+7| |
|+1| |
|+7| |
|
|y=-x+8| |
|-1| |
|+8| |
|
|y=78| |
|0| |
|+78| |
To determine the rate of change and the |y|-intercept, |y| must be isolated on one side of the equation. In other words, the equation must be in the form |y=ax+b|. If it is not the case, we need to isolate the variable |y.|
Here are three examples where we are looking for the rate of change and the |y|-intercept.
Example 1: ||\begin{align} 2y &= 4x+8 \\ \frac{2y}{\color{green}{2}} &= \frac{4x}{\color{green}{2}} + \frac{8}{\color{green}{2}} \\ y &= \color{red}{2}x+\color{blue}{4} \end{align}||
The rate of change of the equation is |\color{red}{2}| and the |y|-intercept is |\color{blue}{4}.|
Example 2: ||\begin{align} y+6x &= 7 \\ y+6x \color{green}{-6x} &= 7 \color{green}{-6x} \\ y &= 7-6x \\ y &= \color{red}{-6}x+\color{blue}{7} \end{align}||
The rate of change of the equation is |\color{red}{-6}| and the |y|-intercept is |\color{blue}{7}.|
Example 3: ||\begin{align} \frac{y}{2}-\frac{6x}{5} &= -3 \\ \frac{y}{2}-\frac{6x}{5} \color{green}{+\frac{6x}{5}} &= -3 \color{green}{+\frac{6x}{5}}\\ \frac{y}{2} &= -3 + \frac{6x}{5} \\ \frac{y}{2} \color{green}{\times 2} &= \left(-3 + \frac{6x}{5}\right) \color{green}{\times 2} \\ y &= -6+\frac{12x}{5} \\y &= \color{red}{\frac{12}{5}}x \color{blue}{-6} \end{align}||
The rate of change of the equation is |\color{red}{\dfrac{12}{5}}| and the |y|-intercept is |\color{blue}{-6}.|
To calculate the rate of change and the initial value, we need to follow these 4 steps.
Identify the dependent and independent variables.
Choose 2 points on the line or 2 ordered pairs from the table of values.
Apply the formula for the rate of change. ||a=\dfrac{\Delta y}{\Delta x}=\dfrac{y_2 - y_1}{x_2 - x_1}||
Replace |a| with the value calculated in the previous step and |x| and |y| with the coordinates of a point, and then isolate |b.|
Note: sometimes, step 4 is not necessary to get the |y|-intercept, since it can be found directly in the graph or the table of values.
In the following example, we consider that the individual’s consumption habits are constant.
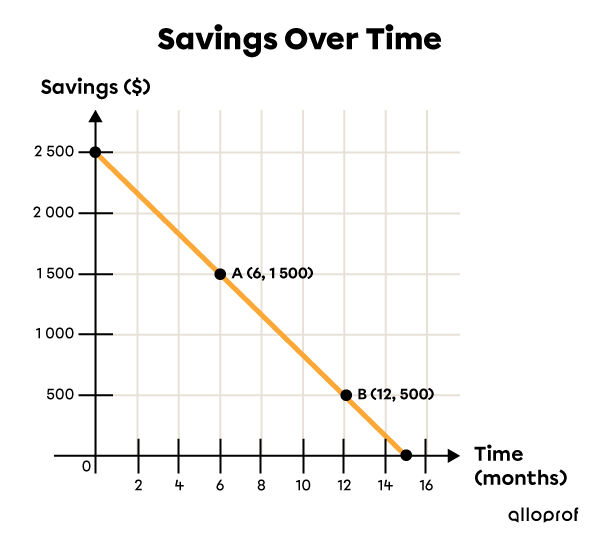
How much money does the individual save per month? (rate of change)
How much did they have saved at the start of the study? (|y|-intercept)
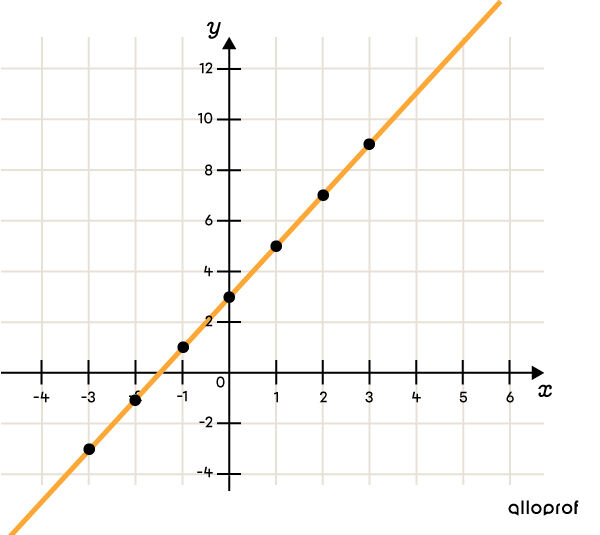
What is the rate of change |(a),| the initial value |(b),| and the equation of the straight line illustrated in the following Cartesian plane?
To calculate the rate of change and the |y|-intercept from a table of values, we follow the same procedure as with the graph. To make it easier, you can draw a graph.
Marc has just opened a print shop. He bought a high-performance photocopier. He decided on the costs below for using the photocopier.
|
Number of photocopies |
|5| |
|10| |
|15| |
|20| |
|40| |
|75| |
|---|---|---|---|---|---|---|
|
Cost |($)| |
|\$ 0.65| |
|\$ 1.30| |
|\$ 1.95| |
|\$ 2.60| |
|\$ 5.20| |
|\$ 9.75| |
What is the price per photocopy?
What is the initial price?
Ginette removes the plug from her bathtub, then she observes the water level in the bath every 2 minutes. The following is the data she collects.
|
Elapsed time (min) |
|2| |
|4| |
|6| |
|8| |
|---|---|---|---|---|
|
Water level (cm) |
|30| |
|22| |
|14| |
|6| |
How quickly does the water level in the tub drop? (rate of change)
What was the water level in the bath when Ginette removed the plug? (|y|-intercept or initial value)
In a word problem, it often happens that the rate of change and the initial value (|y|-intercept) are given directly. In this case, these values can be determined without having to perform any calculations.
At the start of his last trip, Justin's car had |125\ 000| km on the odometer. He maintained an average speed of |100| km/h during the trip. What will be the total mileage on his car after driving for |22| hours?
If the price of gasoline was |\$ 1.12\text{/L}| when I went to get gas, how many litres did I put in my car's fuel tank if I paid |\$ 56?|
In other word problems, it is necessary to use coordinate pairs and calculate the rate of change using them. Then, the initial value (|y|-intercept) is calculated after substituting |a,| |x,| and |y| into the equation of a linear function. In other words, follow the same procedure as when the graph of the situation is available.
Rudolph went camping. He wakes up at 7:00 a.m. and notices that the temperature inside his tent is 15ºC. At 11:00 a.m., he notices that the temperature inside his tent is 21ºC.
How many degrees on average did the temperature inside his tent rise per hour during the morning?
What is the initial value (|y|-intercept) and what does it represent in this situation?
A 100-litre water tank empties at a constant rate in 8 minutes.
Represent the situation on a graph, then give the rate of change, the initial value, and the equation representing the situation.