Subjects
Grades
Adding the parameters |a,| |b,| |h,| and |k| to the basic form |f(x)= \log_c x| results in what is called the standard form (also called the transformed form) of the logarithmic function.
The transformed logarithmic function is usually written like so: ||f(x)=a \log_c (b(x-h)) +k|| where |a,b,h,| and |k| act as parameters.
Note : The parameters |a| and |b| are always non-zero.
The base of the function |(c)| must be greater than |0| and not |1.|
In the following interactive animation, experiment with the values of parameters |a|, |b|, |c|, |h,| and |k| of the logarithmic function. Observe the modifications which take place on the transformed curve (in black) compared to the base function with |c=2| (in green). Observe the effect of modifying the parameters on the function’s properties.
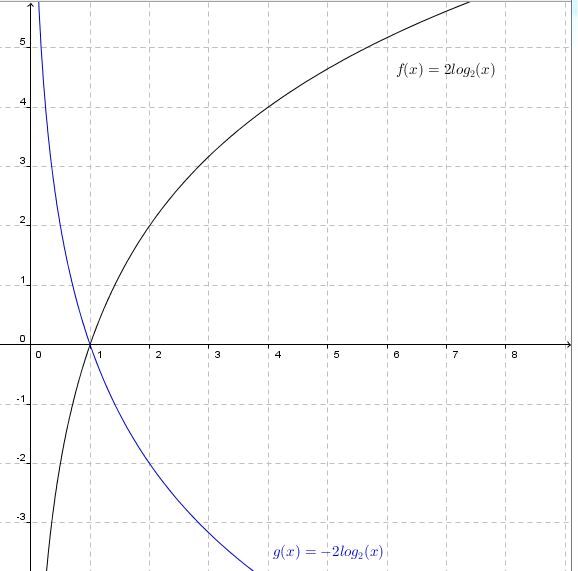
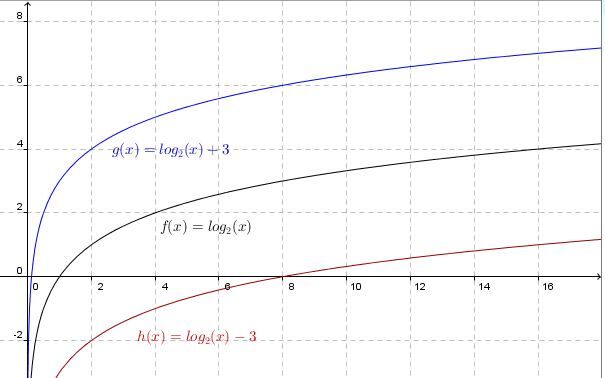
The graph stretches vertically compared to the base function. The greater the absolute value of the parameter |a|, the farther away the curve of the log function is from the |x|-axis.
The graph contracts vertically relative to the base function. The smaller the absolute value of the parameter |a| (closer to |0|), the closer the curve of the log function is to the |x|-axis.

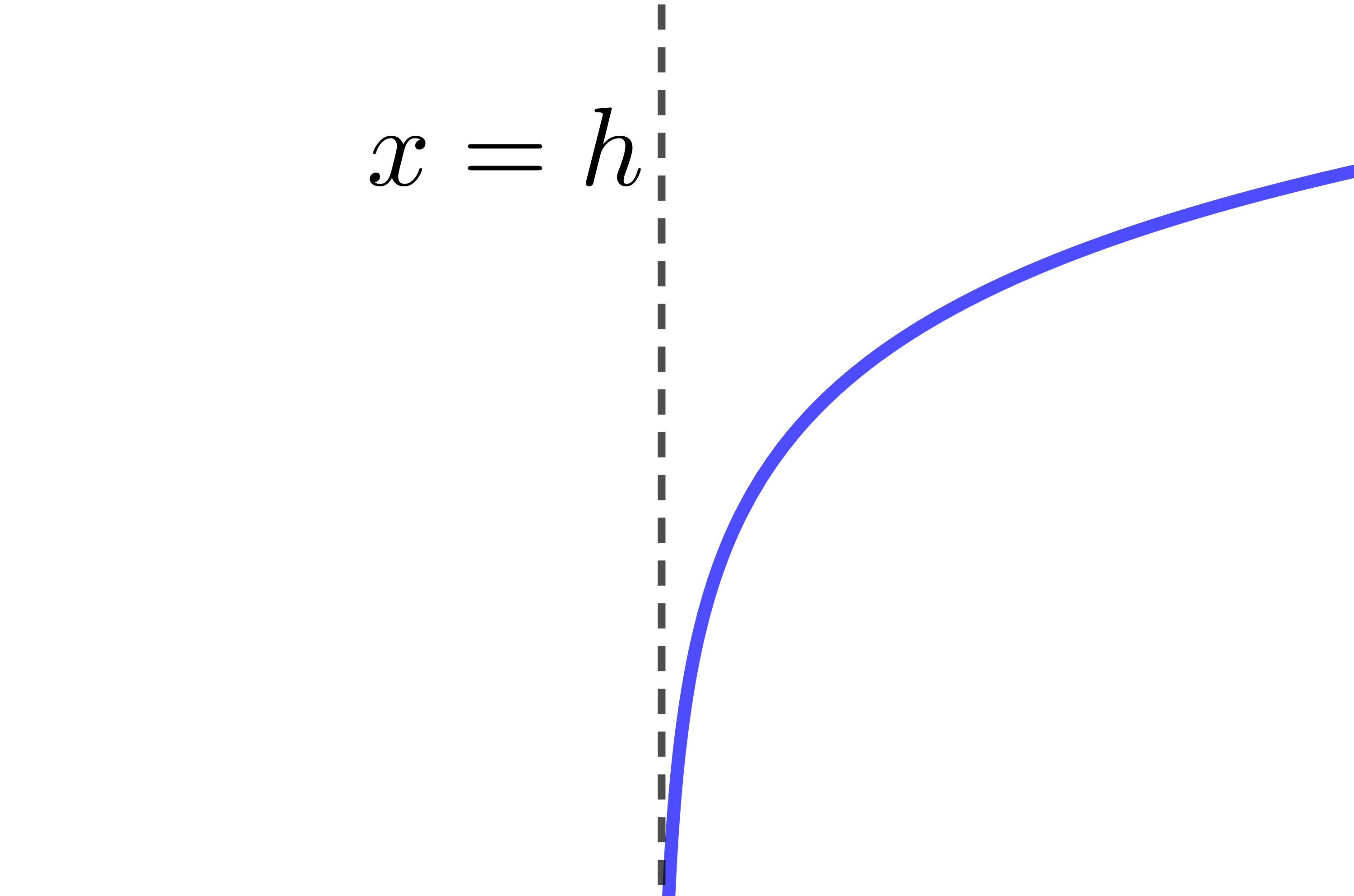
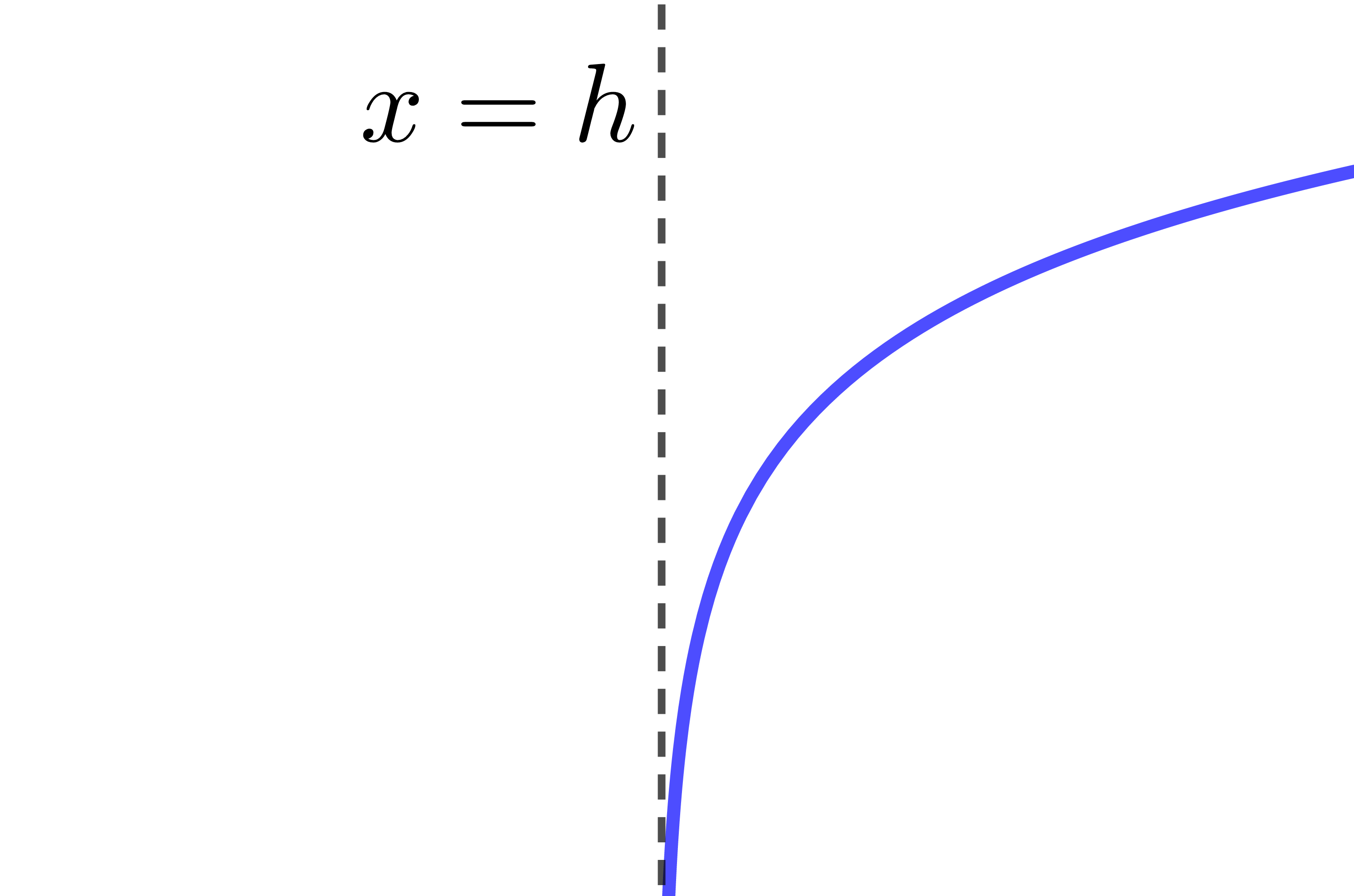
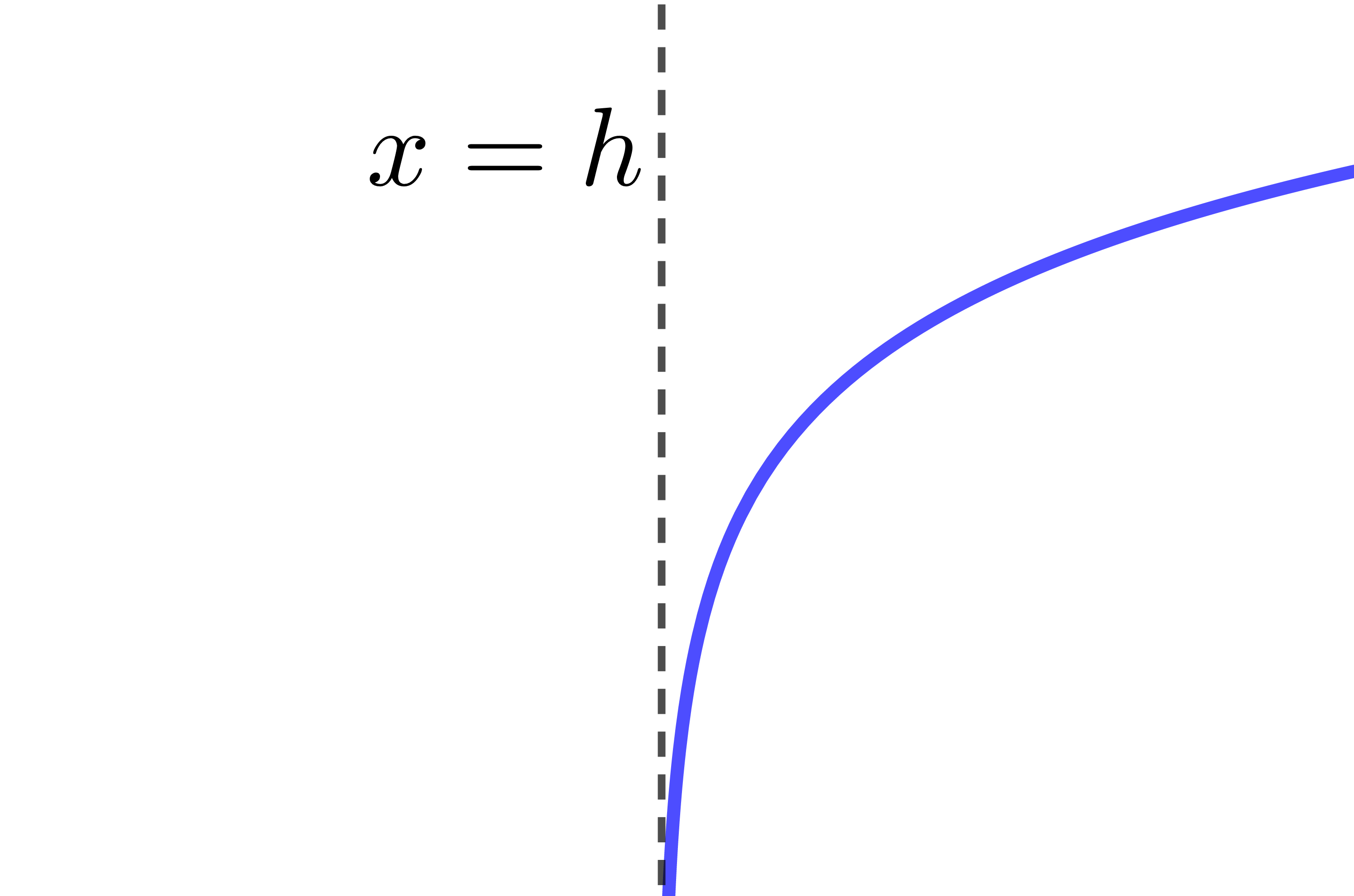
The curve of the logarithmic function is increasing.
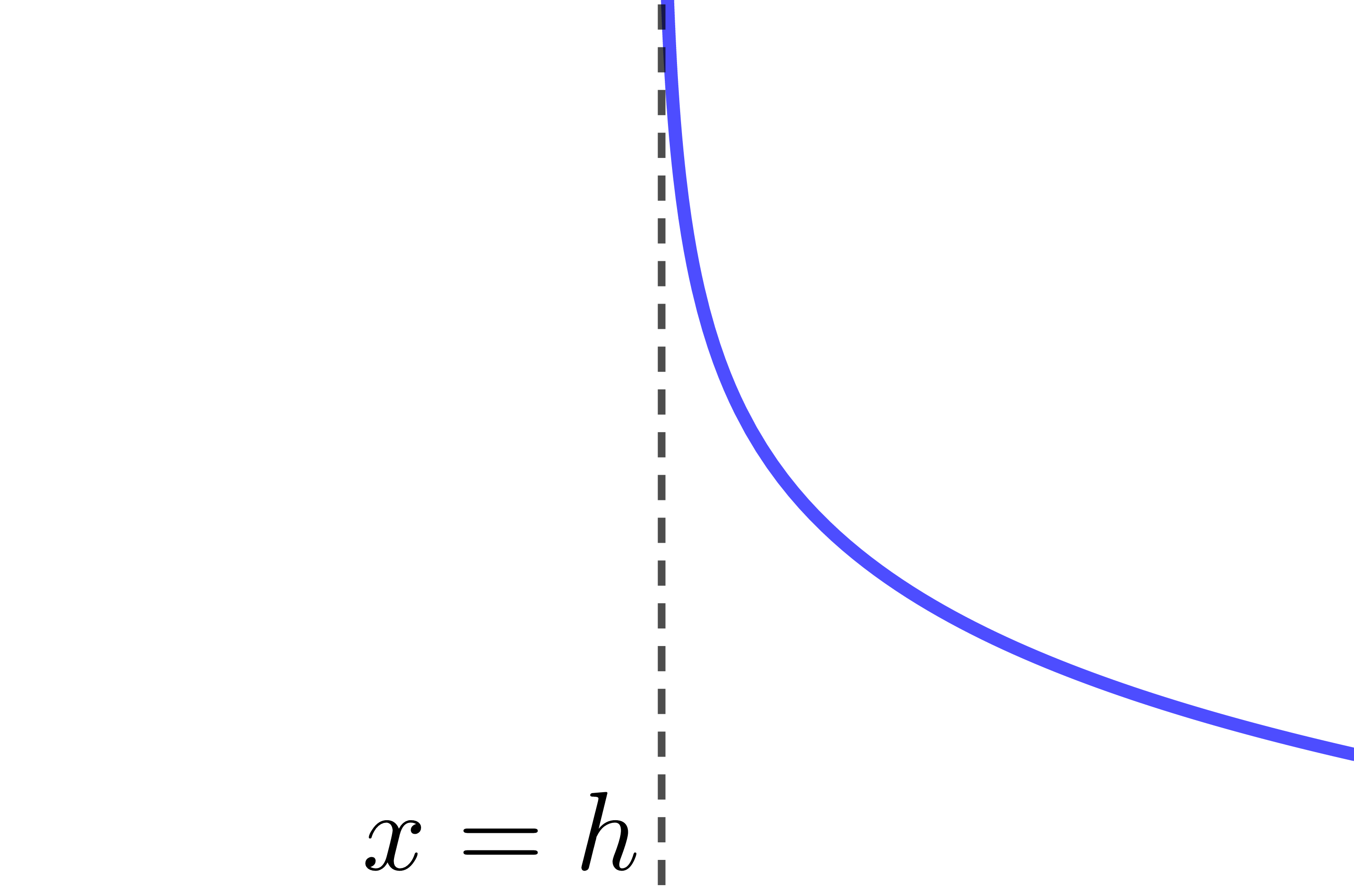
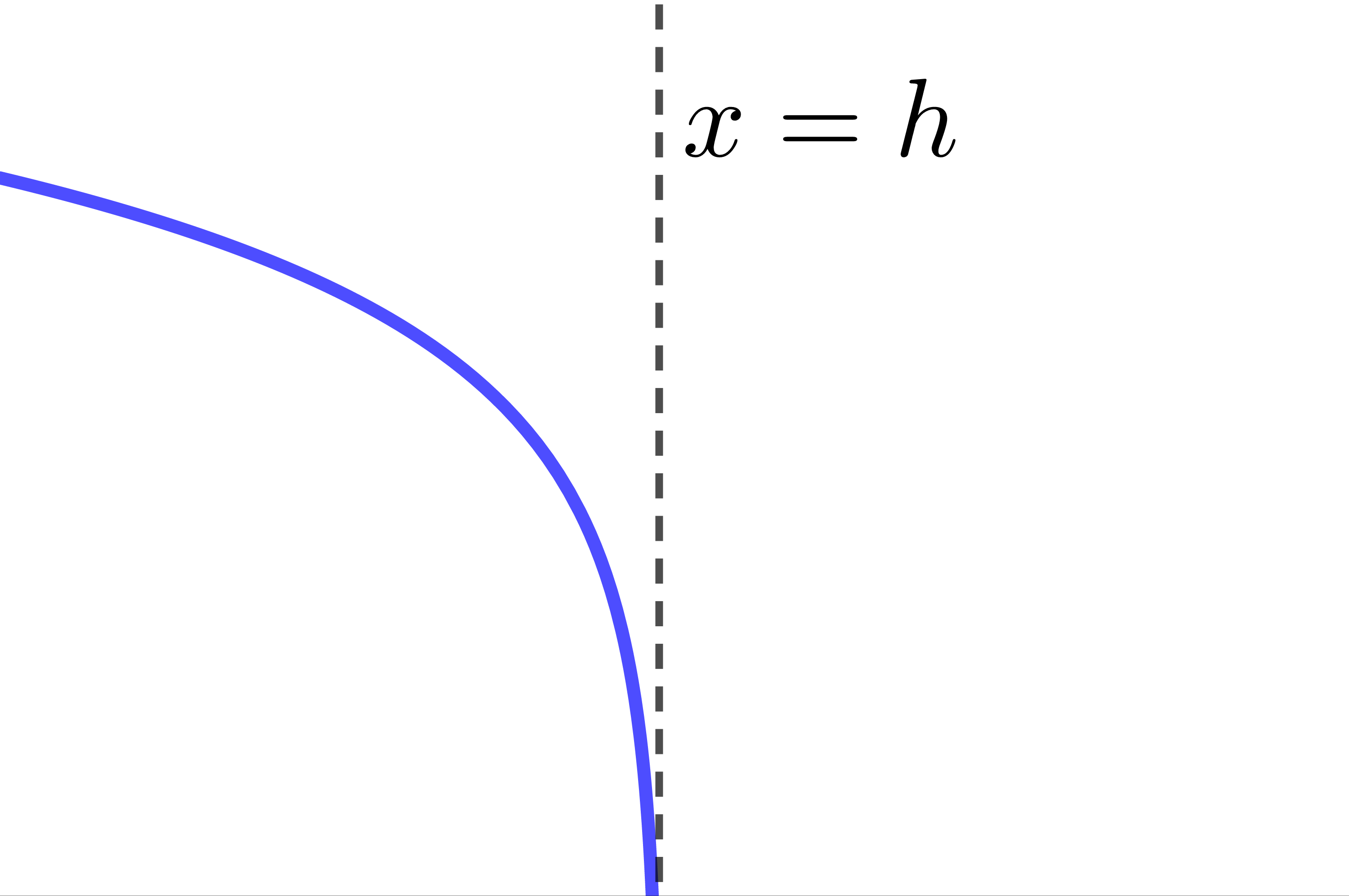
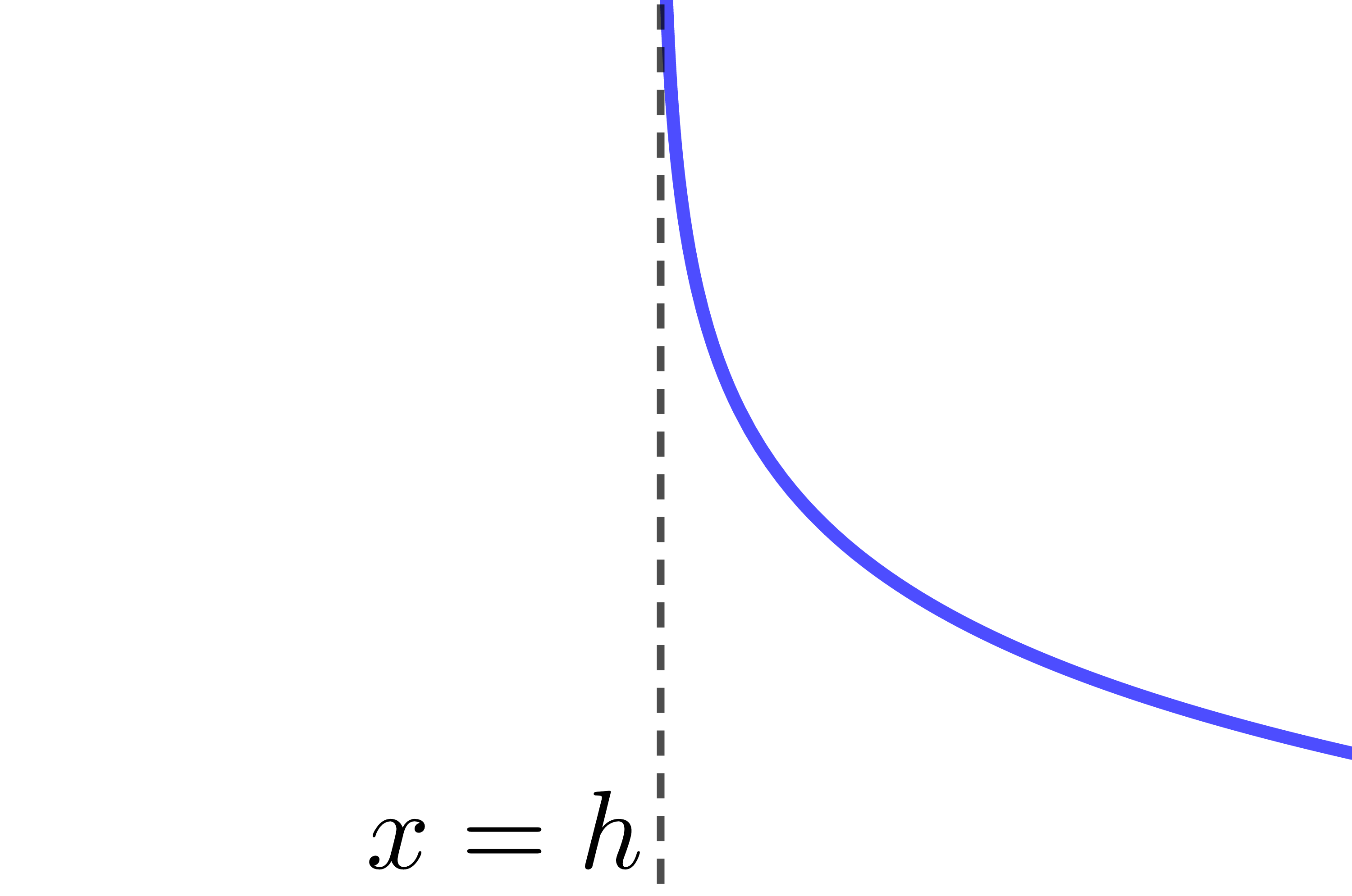
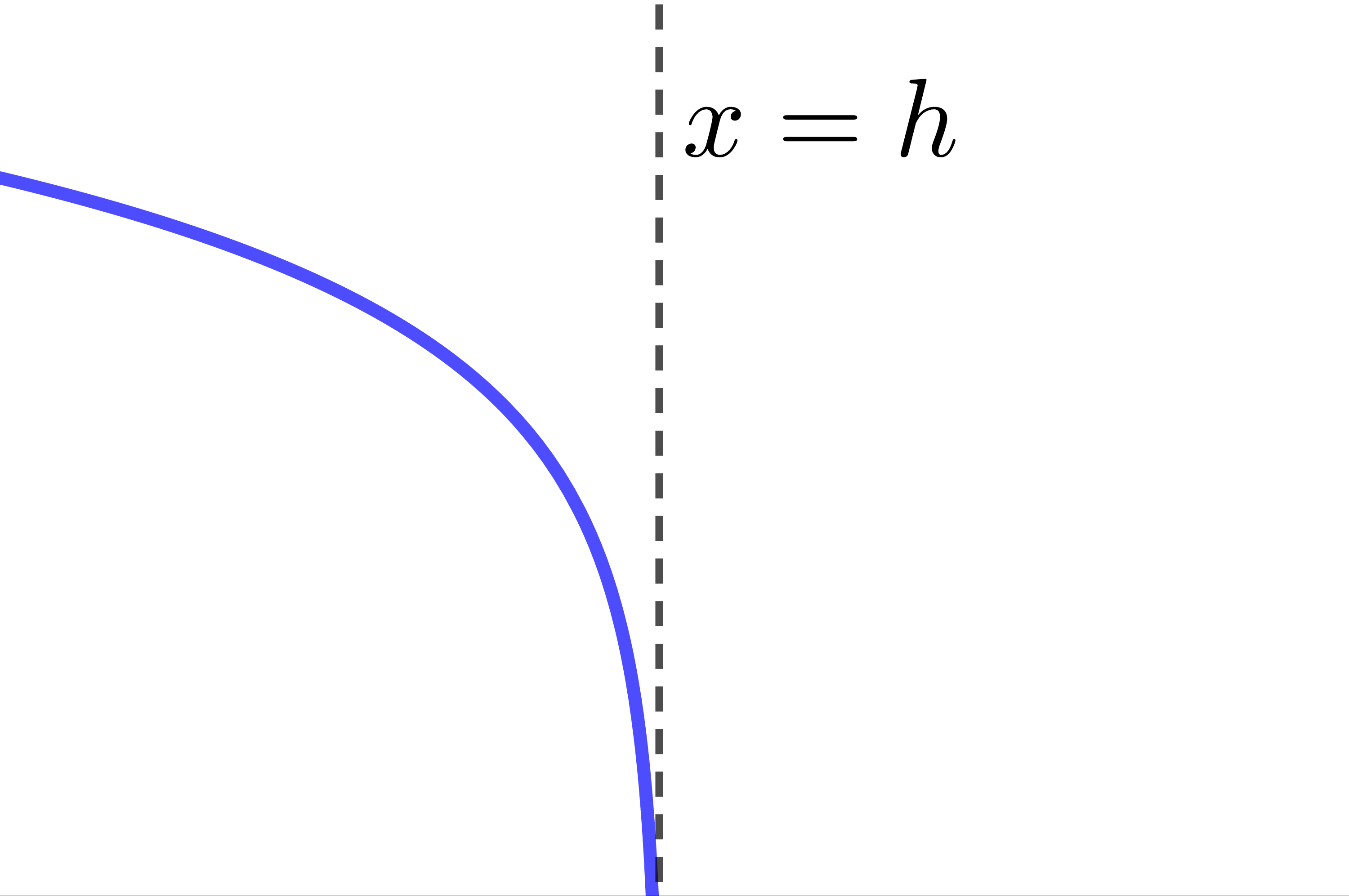
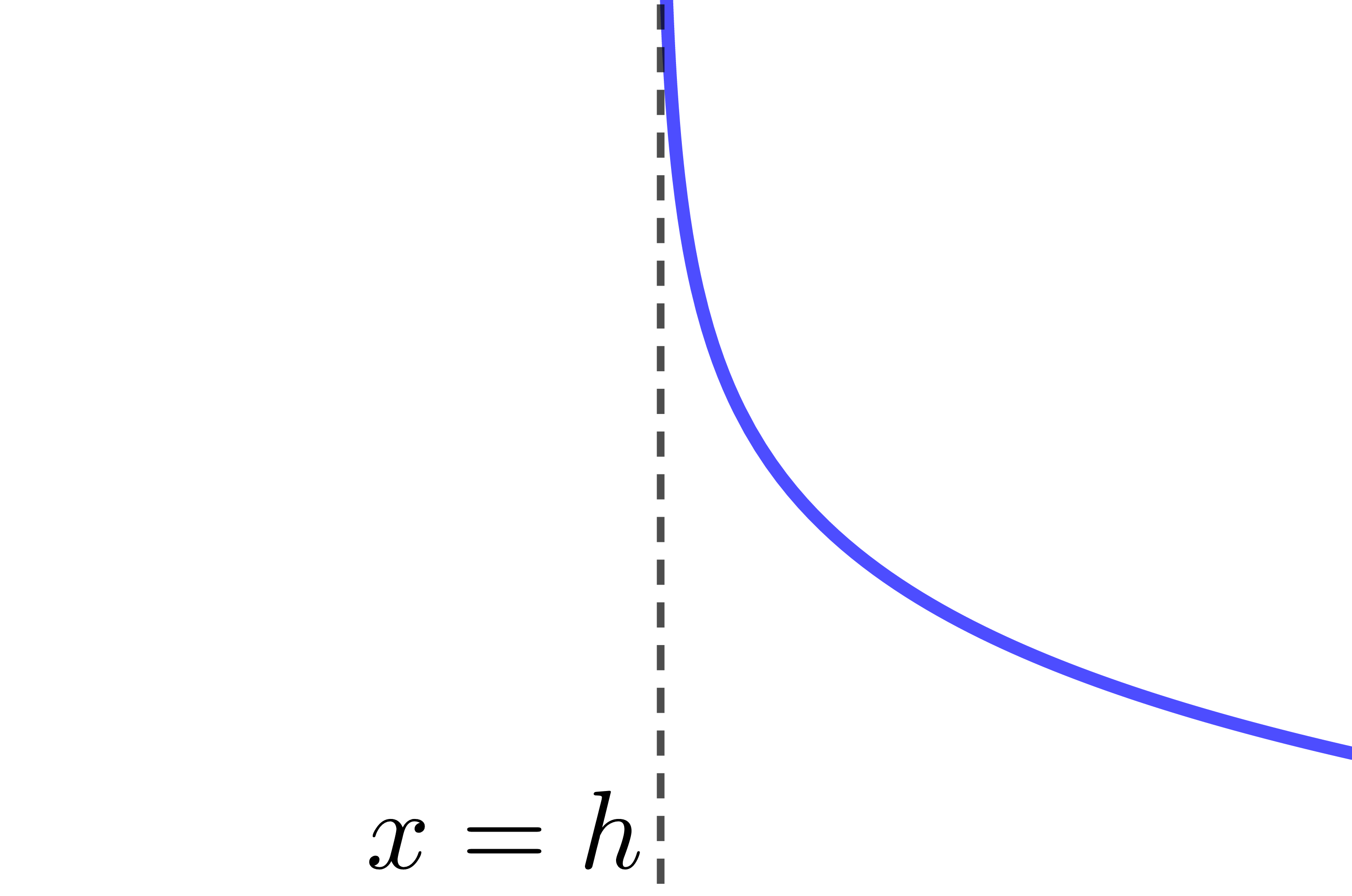
The curve of the logarithmic function is decreasing.
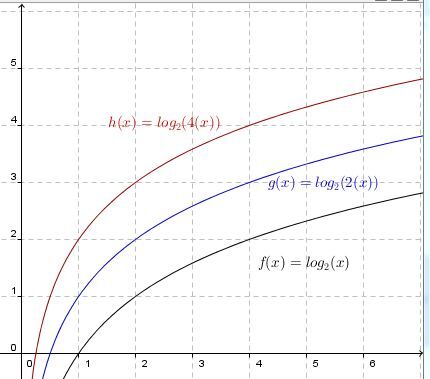
The graph contracts horizontally relative to the base function. The larger the absolute value of the parameter |b|, the more the curve of the logarithm function approaches the |y|-axis.
The graph stretches horizontally relative to the base function. The smaller (close to |0|) the absolute value of the parameter |b|, the farther the curve of the logarithm function is from the |y|-axis.
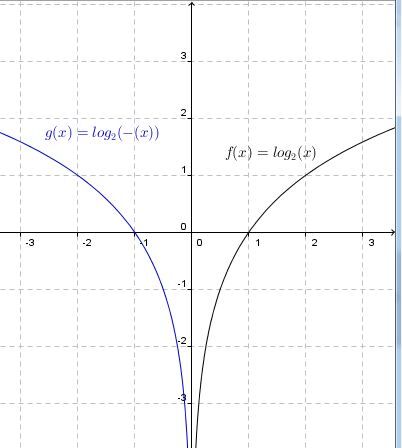
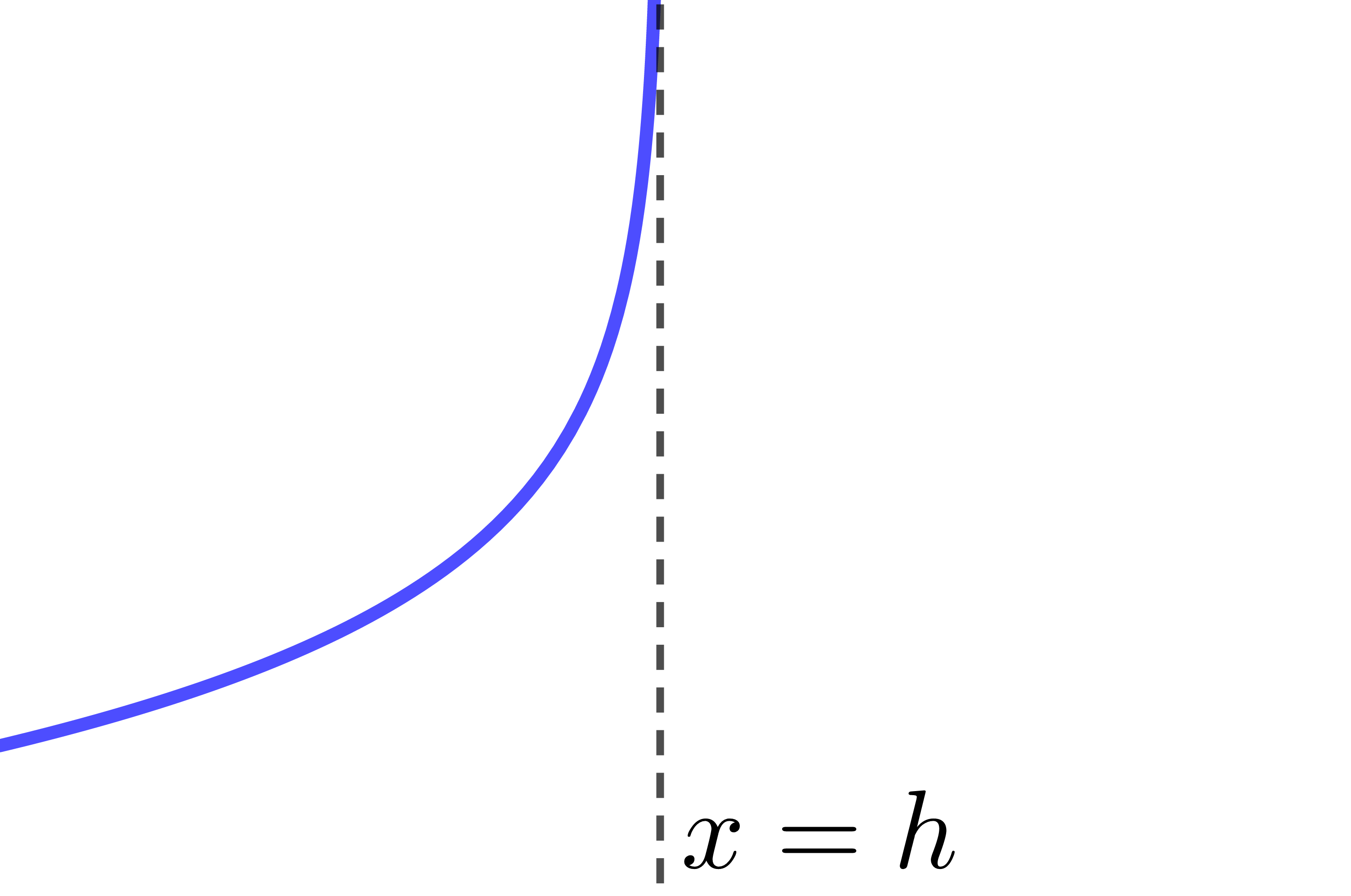
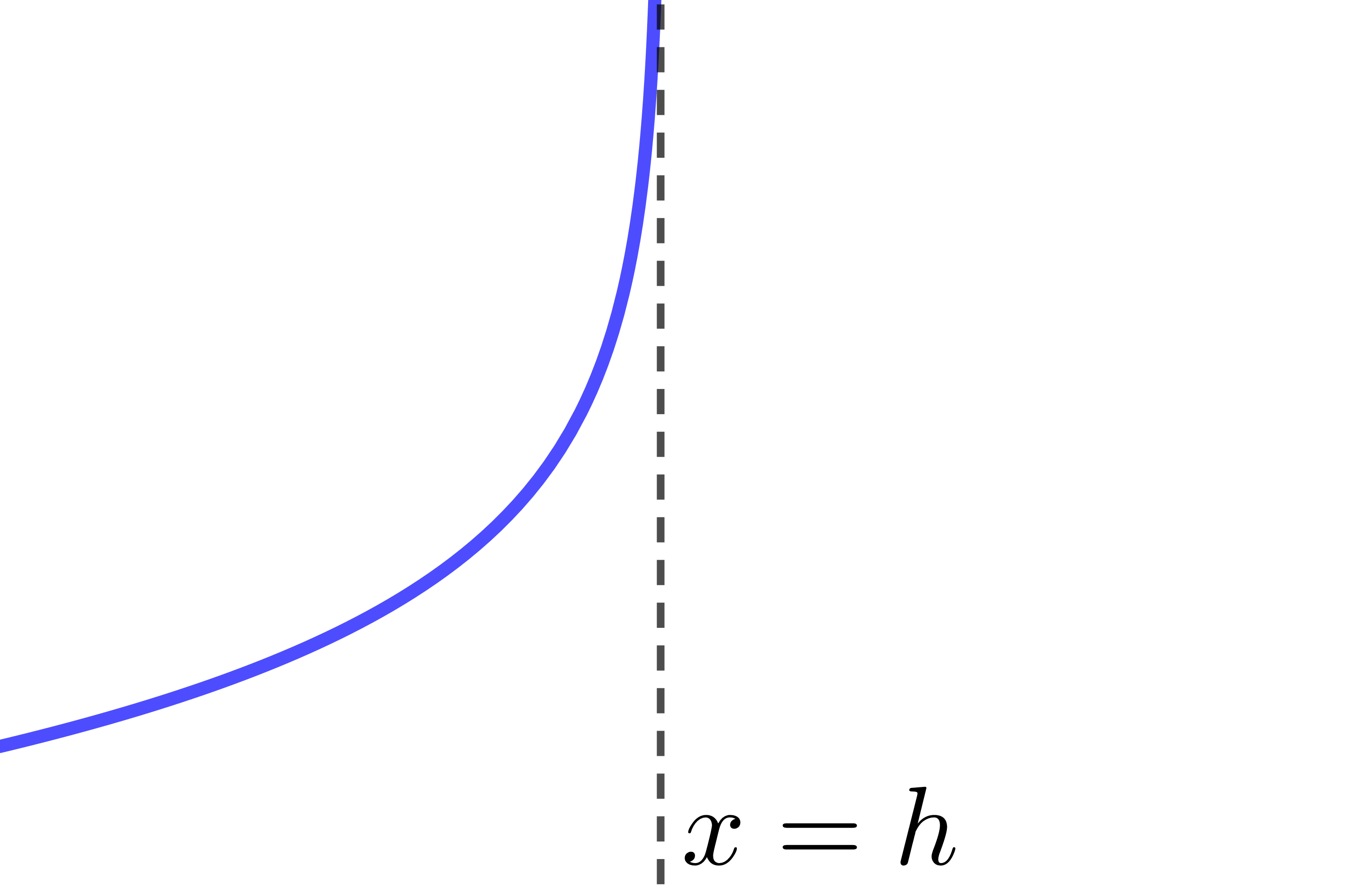
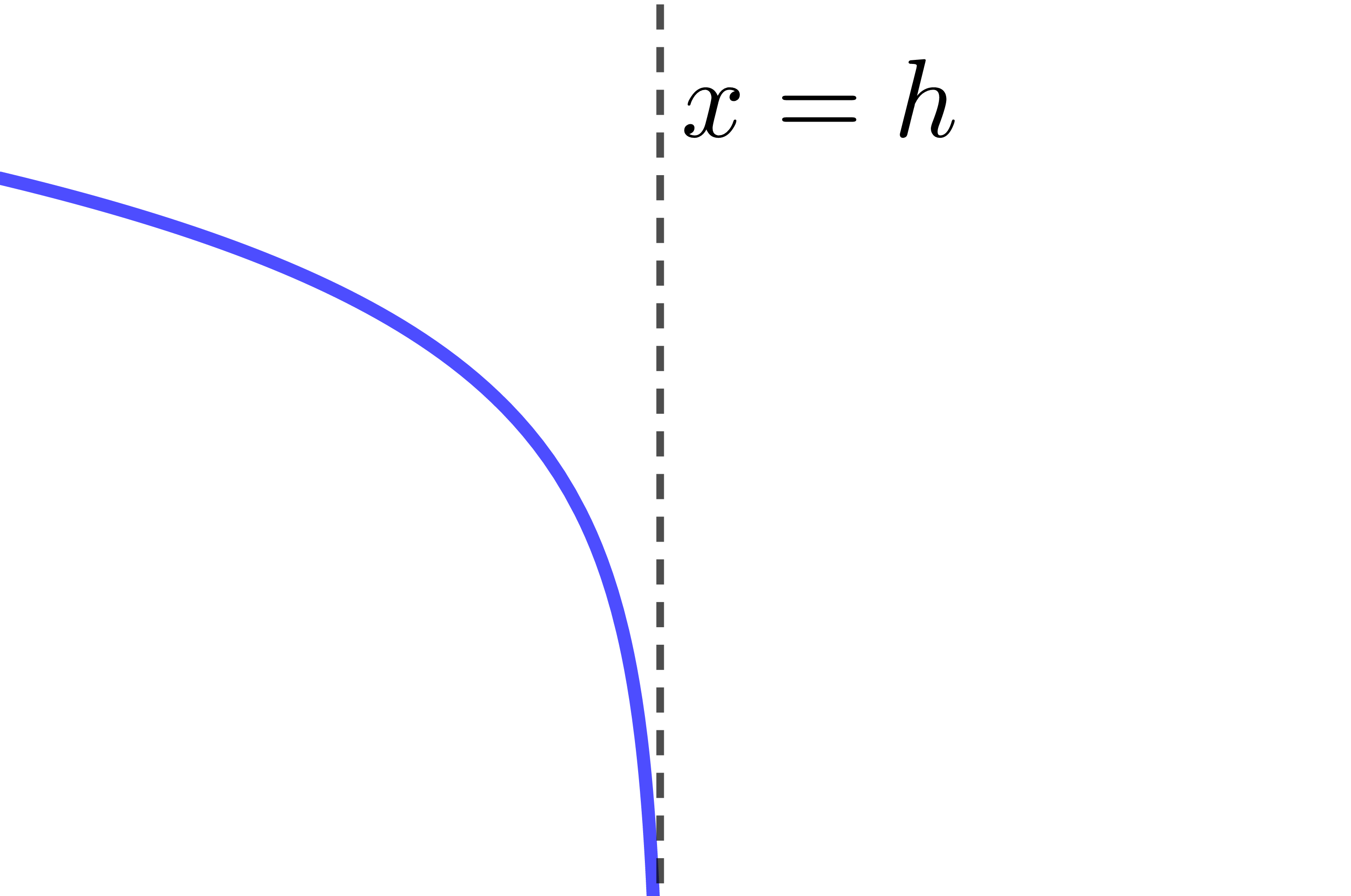
The curve of the logarithmic function is entirely located to the right of the asymptote.
The curve of the logarithmic function is entirely located to the left of the asymptote.
The value of |c| represents the base of the function, that is the multiplying factor present in the exponential function.
The basic function is increasing.
The basic function is decreasing.
Note that |\log_c x = -\log_{\frac{1}{c}} x|.
Using this property, it is possible to transform a logarithm with a base between |0| and |1| into a logarithm with a base greater than |1|.
According to the property |\log_c x = -\log_{\frac{1}{c}} x,| the function |f(x)=-\log_{\frac{1}{2}}x| is equivalent to the function whose equation is |f(x)=\log_2 x.|
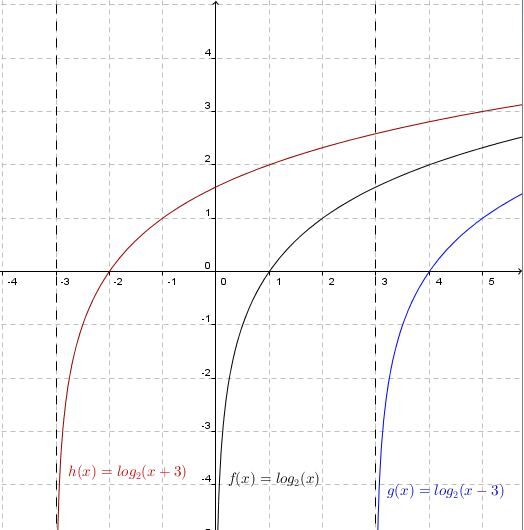
The curve of the logarithmic function moves to the right.
The curve of the logarithmic function moves to the left.
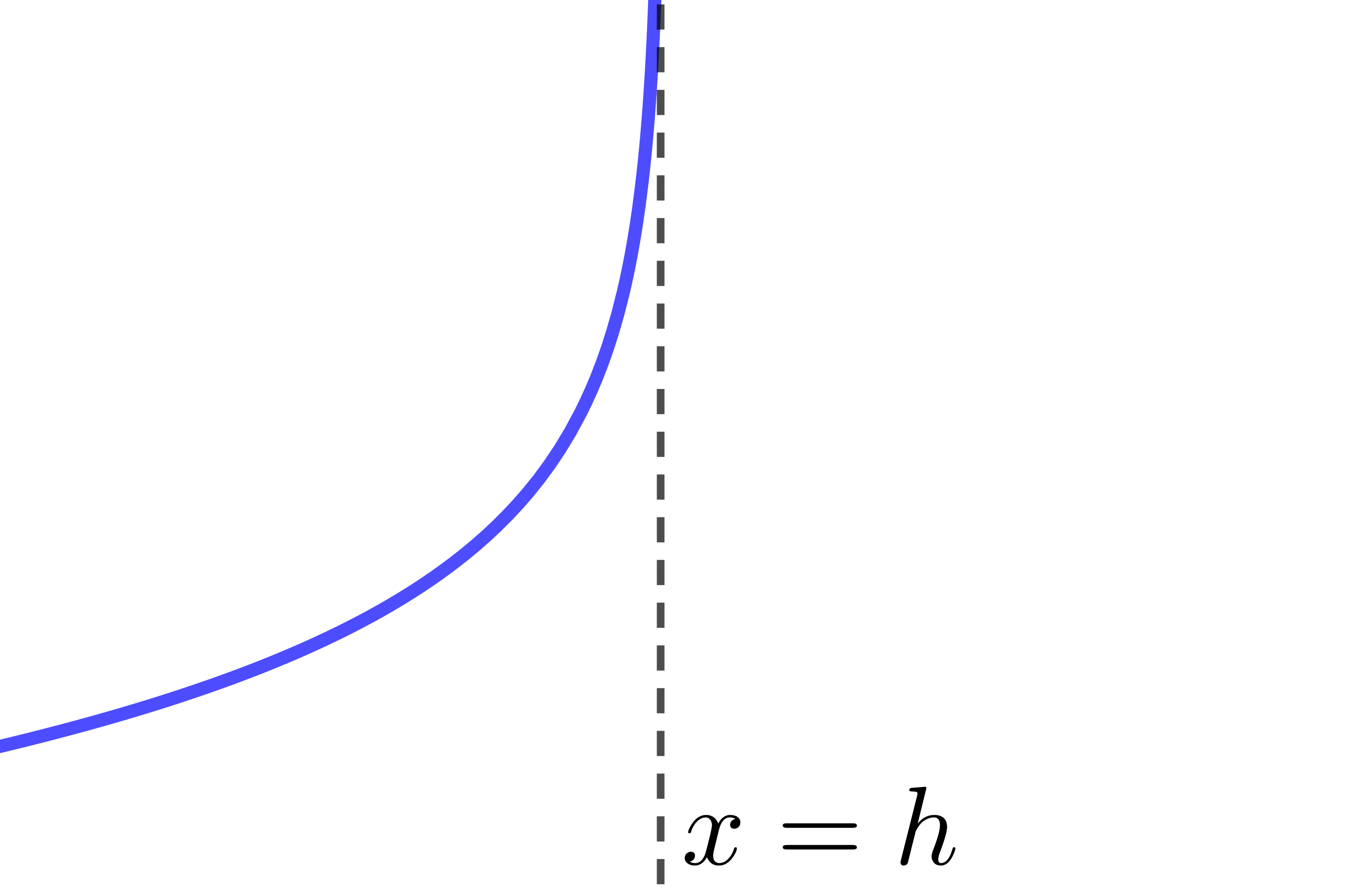
The asymptote of the logarithmic function has the equation |x=h.| Therefore, if the value of the parameter |h| changes, the location of the asymptote also changes.
The curve of the logarithmic function moves upwards.
The curve of the logarithmic function moves downward.
|
|
|a>0| |
|a<0| |
|---|---|---|
|
|b>0| |
 |
 |
|
|b<0| |
 |
 |
|
|
|a>0| |
|a<0| |
|---|---|---|
|
|b>0| |
 |
 |
|
|b<0| |
 |
 |
As seen in the summary table above, certain combinations of parameters give the same result. For example, having |c>1,| |a>0,| and |b>0| is equivalent to having |0<c<1,| |a<0| et |b>0.|
|
|
|b>0| |
|b<0| |
|---|---|---|
|
|c>1| |
 |
 |
|
|0<c<1| |
 |
 |