Subjects
Grades
A rational equation or inequality contains a variable that appears at least once in the denominator.
Since it is impossible to divide by |0,| restrictions must be placed on the variable so that the denominator of the rational fraction is not equal to |0.|
These restrictions must be set before solving the rational equation.
Here are the steps to follow to solve a rational equation.
Isolate the fraction.
Calculate the restrictions.
Perform cross-multiplication.
Solve the equation.
Verify the solution(s).
Write the solution(s).
The cross-multiplication technique, also called the cross-product or product of extremes and means technique, is a quick and effective strategy to solve rational equations. We can also apply inverse operations to obtain the same result.
Solving a rational equation
using cross-multiplication
||\begin{align}\dfrac{4x-5}{3x}&=7\\\dfrac{\color{#FA7921}{4x-5}}{\color{#3A9A38}{3x}}&=\dfrac{\color{#3A9A38}7}{\color{#FA7921}1}\\(\color{#FA7921}{4x-5})\times \color{#FA7921}1&=\color{#3A9A38}{3x}\times \color{#3A9A38}{7}\\4x-5&=21x\end{align}||
Solving a rational equation
using inverse operations
||\begin{align}\dfrac{4x-5}{3x}&=7\\\dfrac{4x-5}{3x}\color{#EC0000}{\times 3x}&=7\color{#EC0000}{\times 3x}\\4x-5&=21x\end{align}||
Solve the equation |\dfrac{2}{x-2}+1=5.|
Isolate the fraction||\begin{align}\dfrac{2}{x-2}+1&=5\\\dfrac{2}{x-2}&=4\end{align}||
Calculate the restrictions ||\begin{align}x-2&\neq0\\x&\neq2\end{align}||
Perform cross-multiplication ||\begin{align}\dfrac{\color{#FA7921}2}{\color{#3A9A38}{x-2}}&=\color{#3A9A38}4\\\color{#FA7921}2&=\color{#3A9A38}4(\color{#3A9A38}{x-2})\end{align}||
Solve the equation ||\begin{align}2&=4x-8\\10&=4x\\2{,}5&=x\end{align}||
Verify the solution
Because |2{.}5\neq 2,| the solution is valid.
Write the solution
The equation’s solution: |\dfrac{2}{x-2}+1=5| is |x=2{.}5.|
There are two ways to verify the solution obtained.
Ensure that the solution respects the restriction determined in step two, as shown in the previous example.
Substitute the solution into the original equation. In the previous example, the variable |x| is replaced in the original equation. Next, make sure that the left-hand side is equivalent to the right-hand side.||\begin{align}\dfrac{2}{\color{#3B87CD}x-2}+1&=5\\ \dfrac{2}{\color{#3B87CD}{2{,}5}-2}+1&\stackrel{?}{=}5\\4+1&\stackrel{?}{=}5\\5&=5\end{align}||The solution is indeed valid.
Solve the equation |\dfrac{3+2x}{x}=8.|
Isolate the fraction
The fraction is already isolated, so move on to the next step.
Calculate the restrictions ||x\neq 0||
Perform cross-multiplication ||\begin{align}\dfrac{\color{#FA7921}{3+2x}}{\color{#3A9A38}x}&=\color{#3A9A38}8\\\color{#FA7921}{3+2x}&=\color{#3A9A38}8(\color{#3A9A38}x)\end{align}||
Solve the equation ||\begin{align}3+2x&=8x\\3&=6x\\0{.}5&=x\end{align}||
Verify the solution
Because |0{.}5\neq 0,| the solution is valid.
Write the solution
The solution of the equation |\dfrac{3+2x}{x}=8| is |x=0{.}5.|
Here is an example where the equation has no solution.
Solve the equation |\dfrac{2x+5}{x-7}=2.|
Isolate the fraction
The fraction is already isolated, so move on to the next step.
Calculate the restrictions ||\begin{align}x-7&\neq0\\x&\neq7\end{align}||
Perform cross-multiplication ||\begin{align}\dfrac{\color{#FA7921}{2x+5}}{\color{#3A9A38}{x-7}}&=\color{#3A9A38}2\\\color{#FA7921}{2x+5}&=\color{#3A9A38}2(\color{#3A9A38}{x-7})\end{align}||
Solve the equation ||\begin{align}2x+5&=2x-14\\0x&=-19\\0&=-19\end{align}|| It’s necessary to stop solving at this step because there’s a false equality: |0| is not equal to |-19.| The equation has no solution.
Verify the solution
Since the equation has no solution, this step is optional. However, the absence of a solution can be verified using the graph of the rational function.
Represent the function as follows: |f(x)=\dfrac{2x+5}{x-7}| . Then, determine for which value(s) of |x| this function is equal to |2,| in other words when |\color{#333FB1}{y=2}.| Since the asymptote of the function is |\color{#333FB1}{y=2}| , a solution (or meeting point) cannot be obtained with the function.
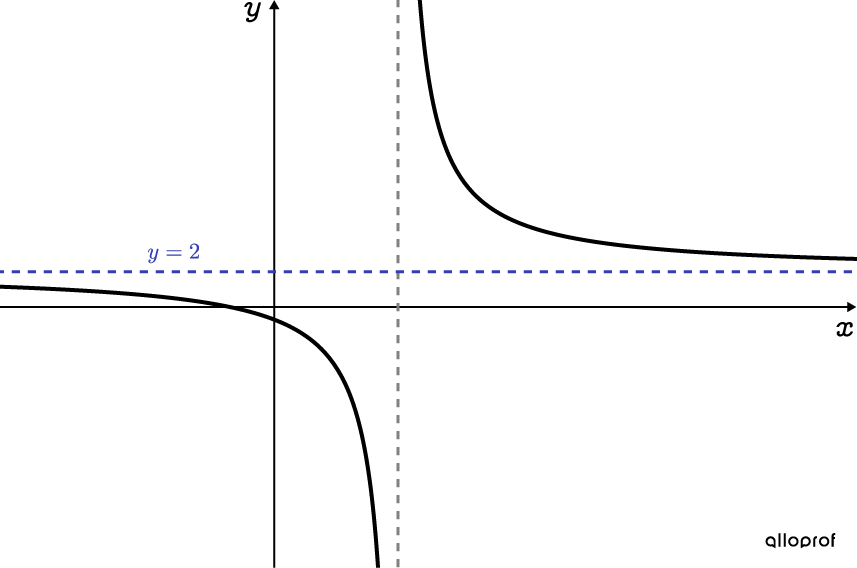
Write the solution set
There is no solution for the equation |\dfrac{2x+5}{x-7}=2.|
When solving a rational equation, sometimes the result is a quadratic equation. This result can mean that the equation has no solution – or it has one or two.
When these situations arise, solve a second-degree equation.
Solve the equation |\dfrac{2x+6}{x-2}=x+3.|
Isolate the fraction
The fraction is already isolated, so move on to the next step.
Calculate the restrictions||\begin{align}x-2&\neq 0\\x&\neq 2\end{align}||
Perform cross-multiplication ||\begin{align}\dfrac{\color{#FA7921}{2x+6}}{\color{#3A9A38}{x-2}}&=\color{#3A9A38}{x+3}\\\color{#FA7921}{2x+6}&=(\color{#3A9A38}{x-2})(\color{#3A9A38}{x+3})\\2x+6&=x^2+x-6\end{align}||
Solve the equation
The previous step resulted in a quadratic equation. Solve it using the quadratic formula.||\begin{align}2x+6&=x^2+x-6\\0&=x^2-x-12\end{align}||||\begin{align}x&=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}\\\\&=\dfrac{-(-1)\pm\sqrt{(-1)^2-4(1)(-12)}}{2(1)}\\\\&=\dfrac{1\pm\sqrt{49}}{2}\\\\x&\in\{-3,4\}\end{align}||
Verify the solutions
Since |-3\neq 2| and |4\neq 2,| the solutions are valid.
Write the solution set
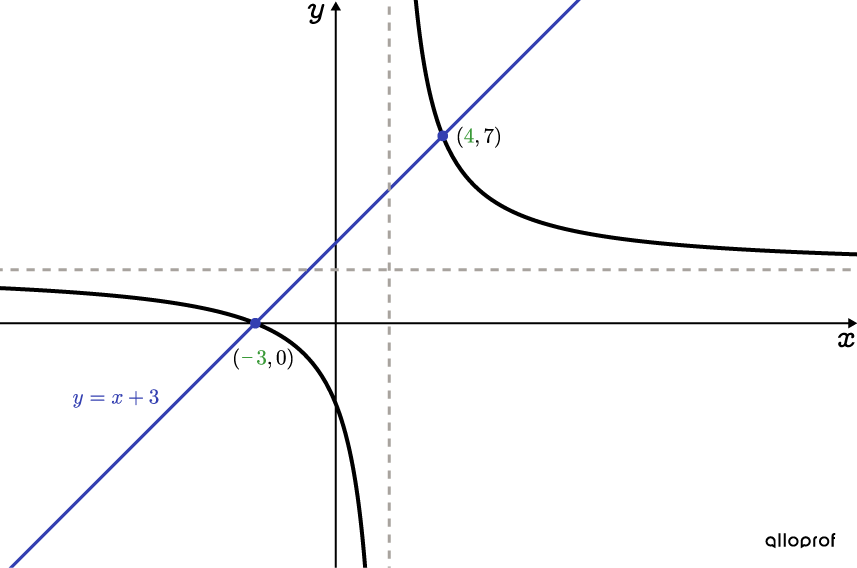
The solution set of the equation |\dfrac{2x+6}{x-2}=x+3| is |x\in\left\{-3,4\right\}.|
The solution set can be clearly seen using a graphical representation. First, draw the function |f(x)=\dfrac{2x+6}{x-2}| , then draw the line with equation |\color{#333FB1}{y=x+3}.| Since the line is oblique and not horizontal, there are two points of intersection. The |\color{#3A9A38}x| -coordinate of these points corresponds to the solutions determined in step 4.
To solve a rational inequality, apply the same steps as for a rational equation.
Replace the inequality symbol with the equal symbol.
Isolate the fraction.
Calculate the restrictions.
Perform cross-multiplication.
Solve the equation.
Verify the solution of the equation.
Determine the solution set of the inequality using a graph or number line.
Solve the inequality |\dfrac{3}{x-1}+4\geq 6.|
Replace the inequality symbol with the equal symbol||\dfrac{3}{x-1}+4=6||
Isolate the fraction||\dfrac{3}{x-1}=2||
Calculate the restrictions||\begin{align}x-1&\neq 0\\x&\neq1\end{align}||
Perform cross-multiplication||\begin{align}\dfrac{\color{#FA7921}3}{\color{#3A9A38}{x-1}}&=\color{#3A9A38}2\\\color{#FA7921}3&=\color{#3A9A38}2(\color{#3A9A38}{x-1})\end{align}||
Solve the equation||\begin{align}3&=2x-2\\5&=2x\\2{.}5&=x\end{align}||
Verify the solution of the equation
Because |2{.}5\neq 1,| the solution is valid.
Determine the solution set of the inequality
Draw the graph of the rational function to determine the solution set.
The vertical asymptote |x=1| corresponds to the restriction determined in step 3.
Draw the function |f(x)=\dfrac{3}{x-1}+4,| then draw a horizontal line at |\color{#333FB1}{y=6}.| This gives the coordinates of the point of intersection |(\color{#3A9A38}{2{.}5},6)| whose |\color{#3A9A38}x| coordinate corresponds to the solution determined in step 5.
We are looking for the values of |x| for which |f(x)\geq 6,| therefore, those which are greater than or equal to |6.| These values are shown in green on the following graph.
By analyzing the graph, we see that the solution set is between |1| and |2{.}5.|
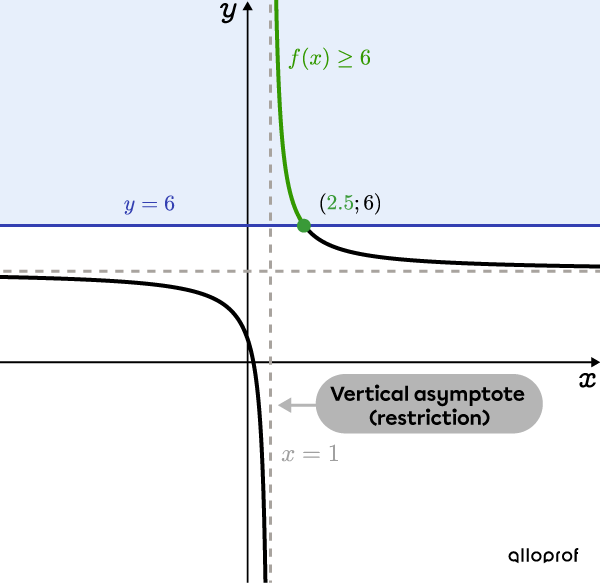
Answer: The solution set is |x\in \left]1, 2{.}5\right].|
Note: Since |x\neq 1| , it must be excluded from the answer using an open square bracket. |2{.}5| is included, since the inequality sign is |\geq| and not |>.|
The solution set (step 7) can be determined using a number line instead of a graphical representation. Using the previous example, here’s how to do it.
Place the restriction determined in step 3 on a number line. Represent it with an open point, since it is excluded from the solution set.
We also place the solution obtained in step 5. Use a solid point, since this value is included in the solution set (given that the inequality sign is |\geq| ).
|1| and |2{.}5| are called critical values.

These two values of |x| divide the number line into three intervals: |]-\infty, 1[,| |]1; 2{.}5]| , and |[2{.}5,+\infty[.| Therefore, it is necessary to verify by choosing a random value in each of these sections and plugging it into the initial inequality.
For |]-\infty, 1[,| use |x=0.|||\begin{align}\dfrac{3}{\color{#3B87CD}x-1}+4&\geq6\\ \dfrac{3}{\color{#3B87CD}{0}-1}+4&\stackrel{?}{\geq}6\\1&\color{#ec0000}{\not\geq}6\ \end{align}||This gives |1\color{#EC0000}{\not\geq} 6.| This conclusion shows that all values less than |1| cannot be in the solution set.
For |]1;2{.}5]|, use |x=2.|
This gives |7\geq 6.| Since this is true, we conclude that the interval |]1,2{.}5]| is part of the solution set.
For |[2{.}5;+\infty[,| use |x=4.|
This gives |5\color{red}{\not \geq} 6.| The conclusion is that all values greater than |2{.}5| cannot be in the solution set.
The solution set indeed corresponds to that determined using the graph, that is, |x\in \left]1, 2{.}5\right].|
Colour the section that corresponds to the solution set on the number line.

Solve the inequality |\dfrac{-2x}{4x-5}-3<-1.|
Replace the inequality symbol with the equal symbol||\dfrac{-2x}{4x-5}-3=-1||
Isolate the fraction ||\dfrac{-2x}{4x-5}=2||
Calculate the restrictions ||\begin{align}4x-5&\neq0\\4x&\neq5\\x&\neq\dfrac{5}{4}\end{align}||
Perform cross-multiplication||\begin{align}\dfrac{\color{#FA7921}{-2x}}{\color{#3A9A38}{4x-5}}&=\color{#3A9A38}2\\\color{#FA7921}{-2x}&=\color{#3A9A38}2(\color{#3A9A38}{4x-5})\end{align}||
Solve the equation||\begin{align}-2x&=8x-10\\-10x&=-10\\x&=1\end{align}||
Verify the solution of the equation
Since |1\neq \dfrac{5}{4},| the solution is valid.
Determine the solution set of the inequality
Now, draw the graph of the rational function.
The vertical asymptote |x=\dfrac{5}{4}| corresponds to the restriction determined in step 3.
First, draw the function |f(x)=\dfrac{-2x}{4x-5}-3,| then draw a horizontal line at |\color{#333FB1}{y=-1}.| This gives the point of intersection |(\color{#3B87CD}{1},-1)| whose |\color{#3B87CD}x|-coordinate corresponds to the solution determined in step 5.
We are looking for the values of |x| for which |f(x)<-1| , so, those that are less than |-1.| These values are shown in green on the following graph.
By analyzing the graph, we deduce that the solution set corresponds to the values of |x| less than |1| and greater than |\dfrac{5}{4}| (the vertical asymptote).
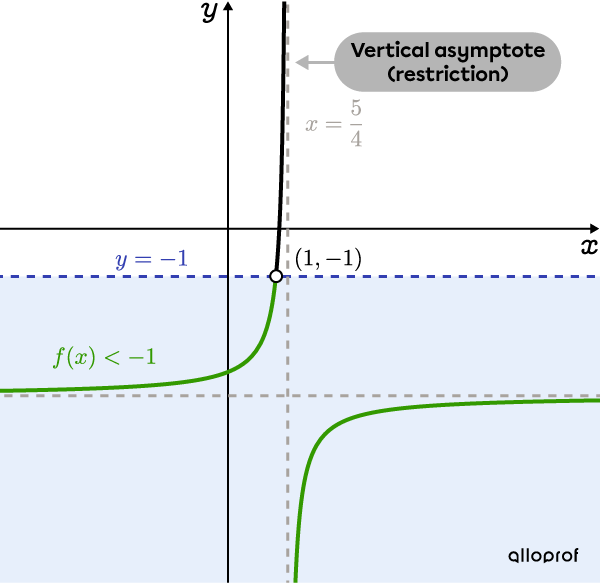
Answer: The solution set is |x\in\left]-\infty,1\right[\cup\left]\dfrac{5}{4},\infty\right[.|
Note: Since |x\neq \dfrac{5}{4}|, it must be excluded from the answer using an open square bracket. |1| is excluded, because the inequality sign is |<| and not |\leq.|