Solving Problems Involving Logarithmic Functions

When athletes first begin to train, they usually make rapid progress. After a while, it is often said that they have “plateaued”. In reality, athletes continue to improve, but their progress becomes less and less noticeable. For this reason, an athlete's performance can be modeled by a logarithmic function.

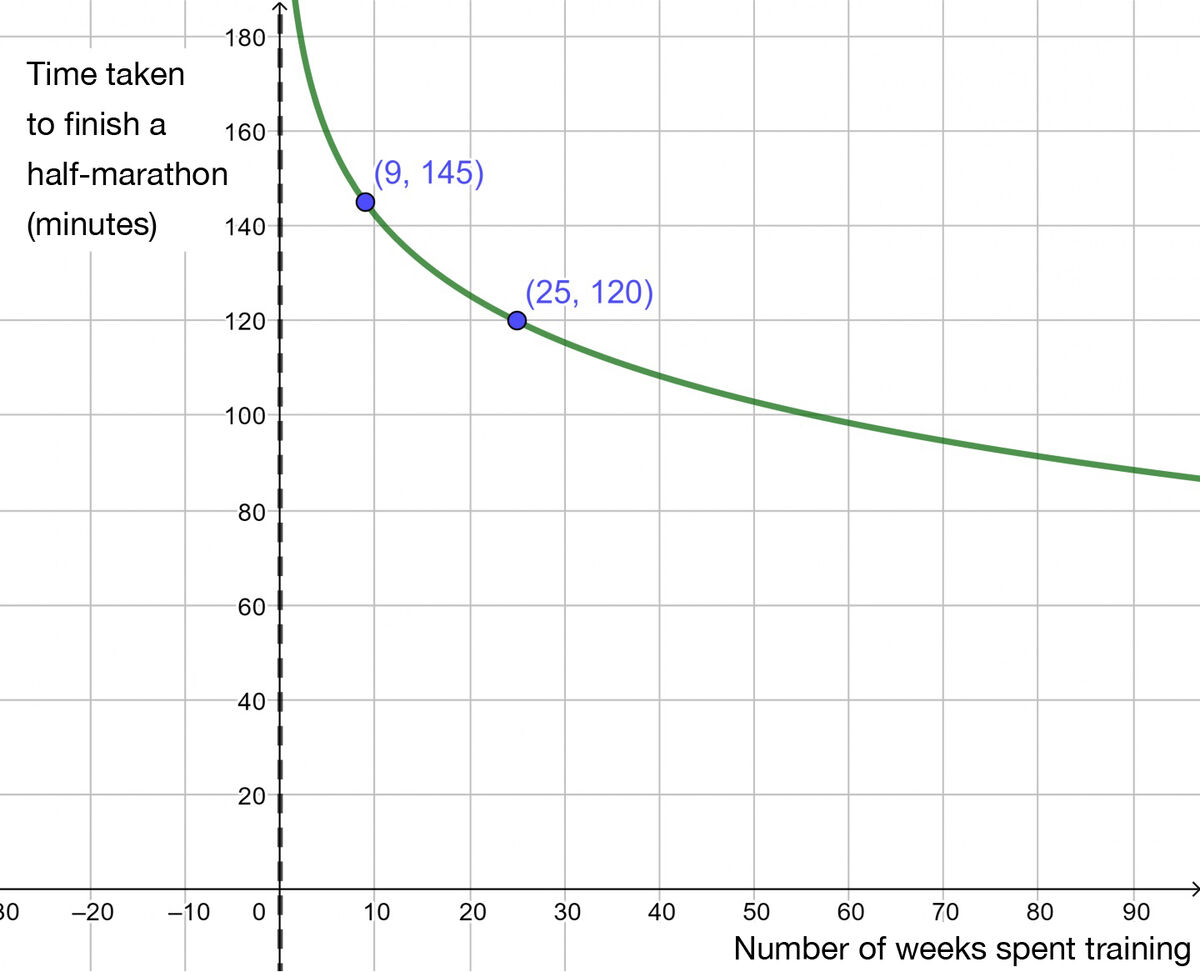
a) What is the approximate time of their half-marathon after |1| full year of training?

b) If the trend continues to follow the same pattern, after how many weeks of training can a runner expect to complete a half-marathon in less than |1| hour and |30| minutes?

To answer the questions in the previous example, it's possible to use the formula |f(x)=\log_c (x-h)+k| to find the equation. Here's how.

1. Replace |h| with the value of the asymptote ||\begin{align} f(x) &= \log_c (x-\color{blue}{h})+k \\f(x) &= \log_c (x-\color{blue}{-0})+k \\f(x) &= \log_c x+k \\ \end{align}||

2. Substitute in each of the points to create a system of equations ||\begin{align} 1^{\text{st}} &\text{ coordinate pair: }(\color{green}{9},\color{red}{145}) &&2^\text{nd} \text{ coordinate pair: }(\color{green}{25},\color{red}{120}) \\\\ \color{red}{f(x)} &= \log_c b\color{green}{x} && \color{red}{f(x)} = \log_c b\color{green}{x} \\\\ \color{red}{145} &= \log_c \color{green}{9}+k && \color{red}{120} = \log_c \color{green}{25}+k && \text{Substitute in }\color{green}{x} \text{ and } \color{red}{y} \\\\ 145&-\log_c 9 = k && 120-\log_c 25 = k && \text{Isolate }k\end{align}||

3. Determine the value of parameter |c| using the comparison method ||\begin{align} k & = k \\\\ 145-\log_c9 &= 120-\log_c 25 \\\\ 25 & = \log_c 9 - \log_c25 \\\\ 25 &= \log_c \left(\dfrac{9}{25}\right) && \text{Law of logarithms}\\\\ c^{25} &= \dfrac{9}{25} && \text{Use exponent laws} \\\\ \sqrt[25]{c^{25}}& = \sqrt[25]{\frac{9}{25}} && \text{Isolate c} \\\\ c & \approx 0.96 \end{align}||

4. Use one of the two points provided to find the value of the parameter |k| ||k = 145-\log_{0.96} 9 \approx 198.8||

Therefore, the equation is |f(x)=\log_{0.96}x+198.8.|

The equation is equivalent to the one found previously. To prove it, we will use it to answer questions a) and b).

---

a)

||\begin{align} f(x) &= \log_{0.96}x + 198.8 \\ f(52) &= \log_{0.96}(52) + 198.8 \\ &\approx 102\ \text{minutes} \end{align}||

Taking the rounding into consideration, this solution is equivalent to the one obtained with the other formula.

---

b)

The inequality is the following. ||90 > \log_{0.96}x+198.8||

Change the greater than sign into an equal sign. || 90 = \log_{0.96}x + 198.8||

Isolate the logarithm. ||-108.8 = \log_{0.96}x||

Rewrite the equation using exponential laws and calculate |x.| ||\begin{align} -108.8 = \log_{0.96}x \ \Longleftrightarrow \ 0.96^{-108.8} &= x \\ 84.9 &\approx x \end{align}||

Once again, after rounding, the answer is equivalent to the one obtained using the other formula.