Subjects
Grades
The Composition of Functions
Concept sheet | Mathematics
Secondary
5
The composition of functions is an operation consisting of replacing the first function’s independent variable by the expression representing the second function’s dependent variable.
Using two real functions |f| and |g| , we define the composition of two functions as follows: |(g\circ f)(x)=g(f(x))| .
Function |(g \circ f)| is called the composite of |g| by |f| . We read the composite |g| of |f| .
You can also have |(f \circ g)(x) = f(g(x))| , which is made up of |f| by |g| . We read the composite |f| of |g| .
In general, two composites are not equal. Therefore, composition is not a commutative operation.
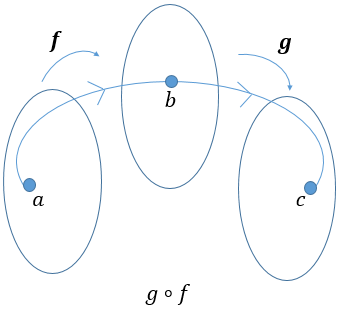
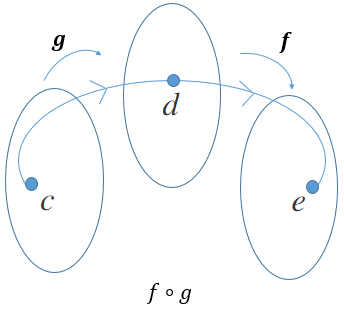
The domain of the composition must consider the restrictions of the two starting functions’ domains.
The symbol sometimes used for multiplication should not be confused with the symbol for the composition of functions.
-
Multiplication: |\cdot|
-
Composition: |\circ|
Algebraic and Graphical Representation of the Composition of Functions
Example 1
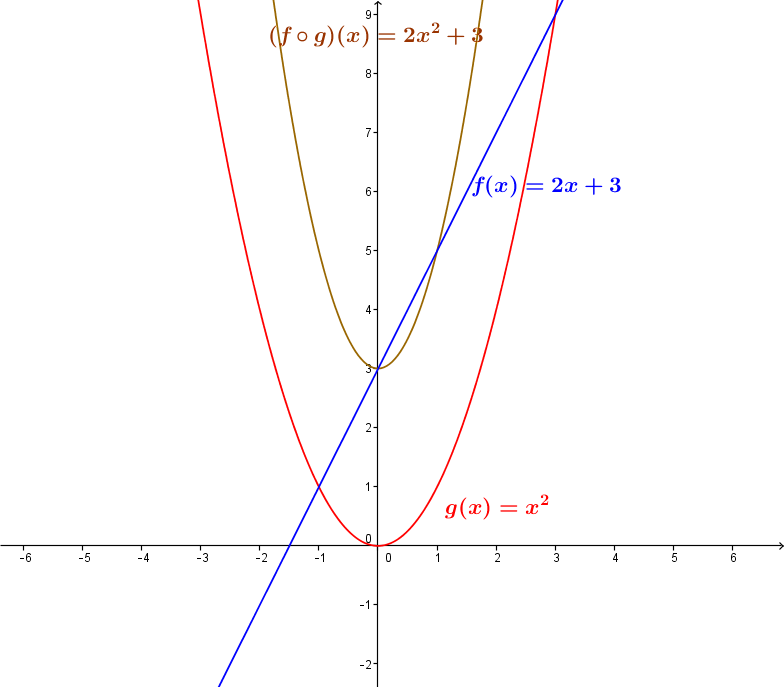
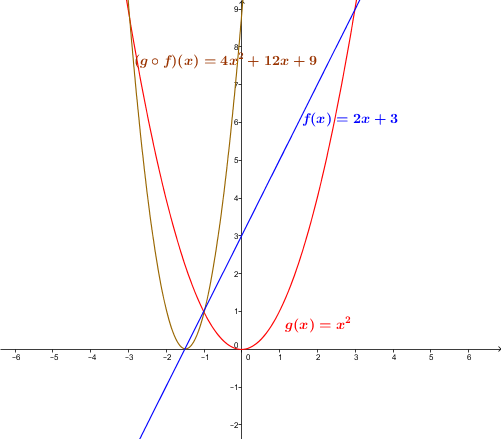
Let the function |f| be defined by |f(x)=2x+3| and the function |g| be defined by |g(x)=x^2.|
The composite |(f \circ g)(x)| is calculated as follows:||\begin{align} (f \circ g)(x) &= f\big(g(x)\big) \\ &=f(x^2) \\ &=2( x^2) + 3 \\ &=2x^2+3 \end{align}||
There is no restriction to add, so the domain of the composition is |\mathbb{R}.|
The composite |(g \circ f)(x)| is calculated as follows:||\begin{align} (g \circ f)(x) &= g\big(f(x)\big) \\ &=g(2x+3) \\ &=(2x+3)^2 \\ &=(2x+3)(2x+3) \\ &=4x^2+12x+9 \end{align}||
There are no restrictions to add, so the domain of the composition is |\mathbb{R}.|
Example 2
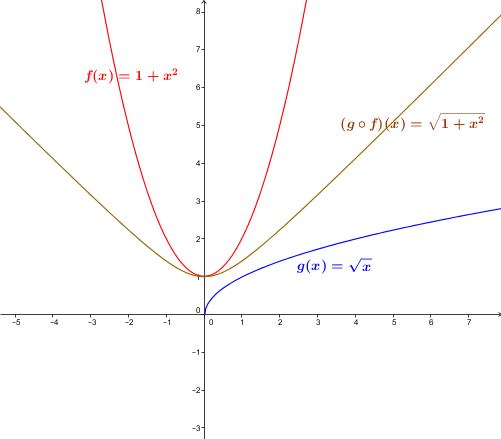
Let the function |f| be defined by |f(x)=1+x^2| and the function |g| be defined by |g(x)=\sqrt{x}.|
The composite |(f \circ g)(x)| is calculated as follows:||\begin{align} (f \circ g)(x) &= f\big(g(x)\big) \\ &= f\left(\sqrt{x}\right) \\ &= 1+\left(\sqrt{x}\right)^2 \\ &=1+x \end{align}||
The domain is the set of positive real numbers. In fact, under the square root, we can only have positive numbers.
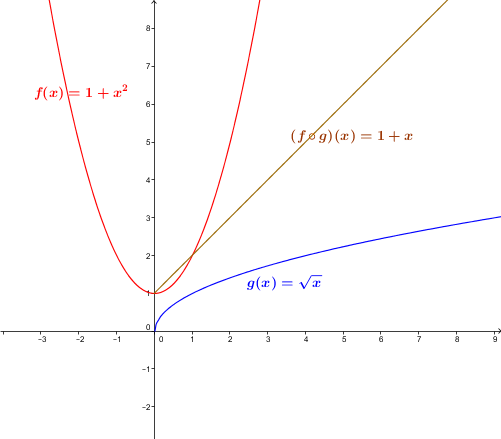
The composite |(g \circ f)(x)| is calculated as follows:||\begin{align} (g \circ f)(x) &= g\big(f(x)\big) \\ &=g\left(1+x^2\right) \\ &=\sqrt{1+x^2} \end{align}||
The domain of the function is the set of real numbers. The function |1+x^2| is always positive, so the square root function is still well defined.
