Subjects
Grades
Operations on functions are performed the same way operations on numbers are performed. Therefore, the difference of functions can be found.
Given two real functions |f| and |g,| the difference between them can be defined as follows. ||(f-g)(x)=f(x)-g(x)||
The domain of the difference function corresponds to the intersection of the domains of the functions in question. If there is a denominator, the restrictions on it must be excluded.
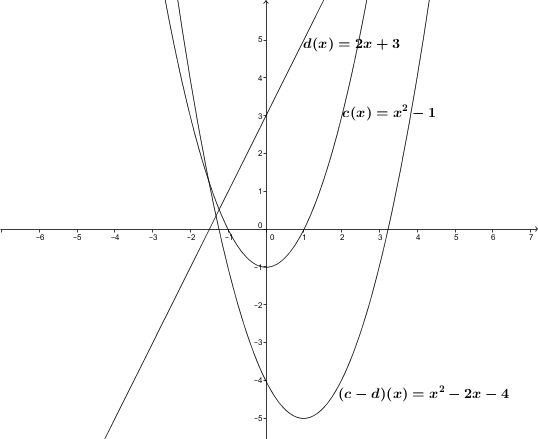
Function |c| is defined by |c(x)=x^{2}-1| and function |d| is defined by |d(x)=2x+3.| The difference in the functions will result in the following. ||\begin{align}(c-d)(x) &= c(x)-d(x) \\ &=(x^{2}-1)-(2x+3) \\ &= x^{2}-1-2x-3 \\ &=x^{2}-2x-4 \end{align}||
The domain of function |c| corresponds to |\mathbb{R}.| The domain of function |d| also corresponds to |\mathbb{R}.| The domain of the function given by |c-d| will correspond to the intersection of the two initial domains. Therefore, this function’s domain will be |\mathbb{R}.|
Function |p| is defined by |p(x)=4\sin\dfrac{\pi}{10}(x)| and function |q| is defined by |q(x)=\dfrac{x}{5}.| The difference in the functions will result in the following. ||\begin{align} (p-q)(x) &= p(x)-q(x) \\ &= 4\sin\dfrac{\pi}{10}(x)-\dfrac{x}{5} \end{align}||
The domain of function |p| corresponds to |\mathbb{R}| and the domain of function |q| corresponds to |\mathbb{R}.| The domain of the function given by |p-q| will correspond to the intersection of the two initial domains. Therefore, this function’s domain will be |\mathbb{R}.|
Function |f| is defined by |f(x)=\dfrac{x-3}{x-4}| and function |g| is defined by |g(x)=\dfrac{x+2}{x^2-16}.| The difference in the functions will result in the following. ||\begin{align} (f-g)(x) &= f(x)-g(x) \\ &= \dfrac{x-3}{x-4}-\dfrac{x+2}{x^2-16} \\ &= \dfrac{x-3}{x-4}-\dfrac{x+2}{(x-4)(x+4)} \\ &= \dfrac{x-3}{x-4}\times \dfrac{x+4}{x+4} -\dfrac{x+2}{(x-4)(x+4)} \\ &= \dfrac{(x-3)(x+4)}{(x-4)(x+4)} -\dfrac{x+2}{(x-4)(x+4)} \\ &= \dfrac{x^2+x-12}{(x-4)(x+4)} -\dfrac{x+2}{(x-4)(x+4)} \\ &= \dfrac{x^2+x-12-(x+2)}{(x-4)(x+4)} \\ &= \dfrac{x^2+x-12-x-2}{(x-4)(x+4)} \\ &= \dfrac{x^2-14}{x^2-16} \end{align}||
The domain of function |f| is |\mathbb{R} \backslash \lbrace 4 \rbrace| and the domain of function |g| is |\mathbb{R} \backslash \lbrace -4,4 \rbrace.| Therefore, the domain of the resulting function is |\mathbb{R} \backslash \lbrace 4 \rbrace \cap \mathbb{R} \backslash \lbrace -4,4 \rbrace = \mathbb{R} \backslash \lbrace -4, 4 \rbrace.|
To find the difference between two functions in a graph, subtract the range of the first function by the range of the second function.
To produce the graph, make a table of values or use the peculiarities of the resulting function.
In the first example, the table of values of the functions |c(x)=x^{2}-1,| |d(x)=2x+3| and |c-d,| would result in the following.
|
|x| |
|c(x)| |
|d(x)| |
|(c-d)(x)| |
|---|---|---|---|
|
|0| |
|-1| |
|3| |
|-4| |
|
|1| |
|0| |
|5| |
|-5| |
|
|2| |
|3| |
|7| |
|-4| |
|
|3| |
|8| |
|9| |
|-1| |
|
|4| |
|15| |
|11| |
|4| |
Since the resultant function is a quadratic function, the associated formulas can be used to find the vertex and the zeros.
Vertex:
|(c-d)(x)=x^{2}-2x-4|
|h=\dfrac{-b}{2a}=\dfrac{-(-2)}{2\times 1}=1|
|\begin{align} k &= (c-d)(h) \\ &= (c-d)(1) \\ &= (1)^{2}-2(1)-4 \\ &=-5 \end{align}|
So |(h,k)= (1,-5).|
Zeros:
|\begin{align} x_{\{1,2\}} &= \dfrac{-b\pm\sqrt{b^{2}-4ac}}{2a} \\ &=\frac{-(-2)\pm\sqrt{(-2)^{2}-4(1)(-4)}}{2(1)} \end{align}|
We find |(-1.24, 0)| and |(3.24, 0).|
The following graph is obtained.