Subjects
Grades
The Role of Parameters in a Cosine Function
Concept sheet | Mathematics
Secondary
5
Table of contents
- Top of page
- Animation for Manipulating Parameters
- Analyzing Parameter |a|
- Vertical Scaling of the Curve by |a|
- Reflection of the Function’s Graph With Respect to the |x|-axis
- Analyzing Parameter |b|
- Horizontal Scaling of the Curve by |\dfrac{1}{b}|
- Analyzing Parameter |h|
- Horizontal Translation of the Whole Function
- Analyzing Parameter |k|
- Vertical translation of the whole function
- See Also
Adding the parameters |a,| |b,| |h,| and |k| to the basic function |f(x)=\cos(x)| results in what is called the standard form (also called the transformed form) of the cosine function.
The standard form of a cosine function is: ||f(x)=a \cos\big(b(x-h)\big)+k|| where |a,| |b,| |h,| and |k| are real numbers that function as parameters.
Note: The parameters |a| and |b| are always non-zero.
Animation for Manipulating Parameters
Experiment with the parameters |a,| |b,| |h,| and |k| in the interactive animation to see their effects on the cosine function. Observe the changes that take place on the transformed curve (in green) compared to the base function (in black). Afterwards, keep reading the concept sheet to learn more about each of the parameters.
Analyzing Parameter |a|
Vertical Scaling of the Curve by |a|
When |{\mid}a{\mid}>1|
The larger the absolute value of the parameter |a|, the greater the amplitude of the cosine function.
When |0< {\mid}a{\mid} < 1|
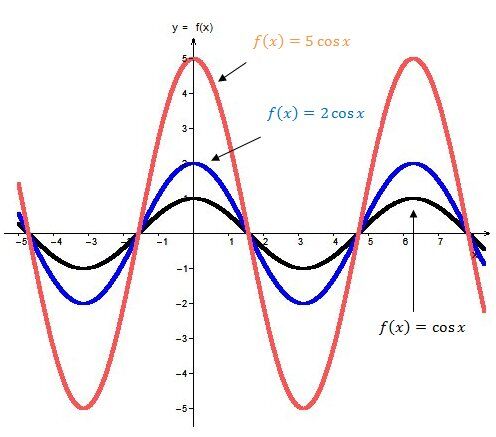
The smaller the absolute value of the parameter |a| (nearer |0|), the smaller the amplitude of the cosine function.
Reflection of the Function’s Graph With Respect to the |x|-axis
When |a| is positive |(a>0)|
The point |(h,k+a)| is a maximum of the curve and the function decreases after this point.
When |a| is negative |(a<0)|
The point |(h,k+a)| is a minimum of the curve and the function increases after this vertex.
Analyzing Parameter |b|
Horizontal Scaling of the Curve by |\dfrac{1}{b}|
When |{\mid}b{\mid} >1|
The larger the absolute value of the parameter |b|, the smaller the period and the smaller the distance between two maxima or minima of the function.
When |0< {\mid}b{\mid} <1|:
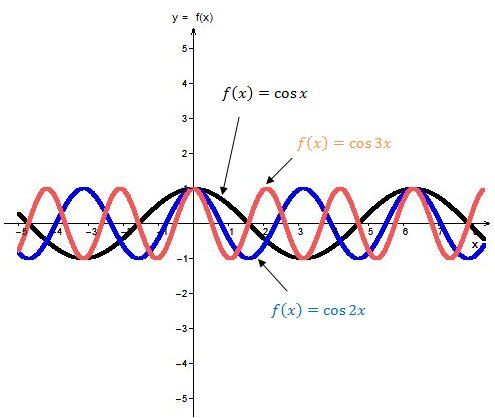
The smaller the absolute value of the parameter |b| (closer to |0|), the greater the period and the distance between two maxima or two minima of the function.
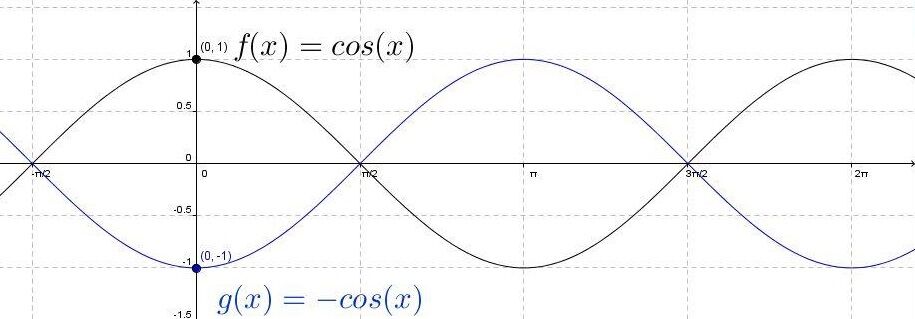
A cosine function with the same value of |b|, but the opposite sign, superimposes onto the other function.
Analyzing Parameter |h|
Horizontal Translation of the Whole Function
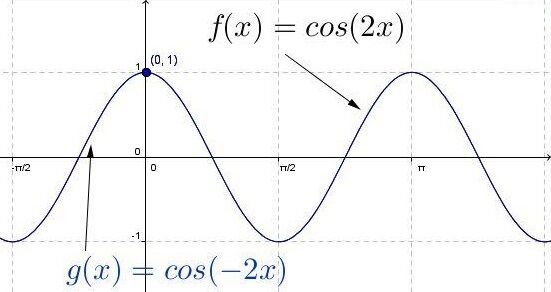
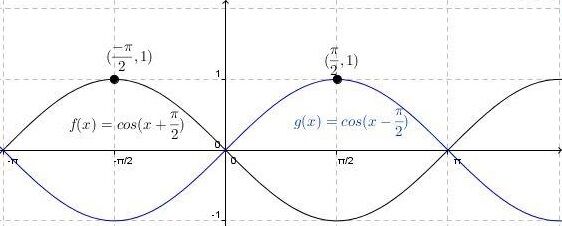
The parameter |h| is responsible for the horizontal displacement of the curve. This is also called the phase shift in a sinusoidal function.
When |h| is positive |(h>0)|
The curve of the cosine function moves to the right.
When |h| is negative |(h<0)|
The curve of the cosine function moves to the left.
Analyzing Parameter |k|
Vertical translation of the whole function
When |k| is positive |(k>0)|
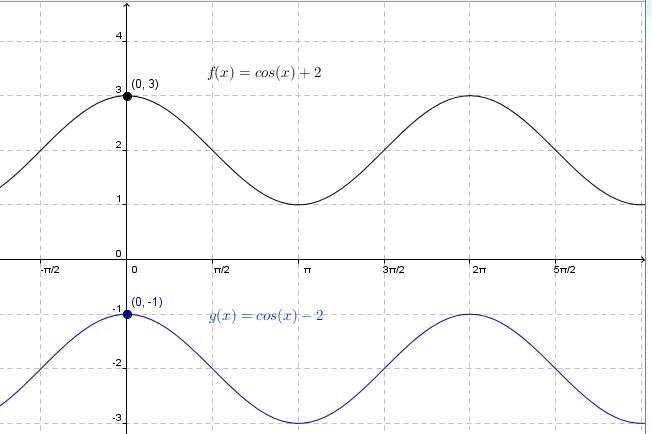
The cosine function moves upwards.
When |k| is negative |(k<0)|
The cosine function moves downwards.
