Subjects
Grades
The Trigonometric Ratio of Tangent
Concept sheet | Mathematics
Secondary
4
The tangent ratio is one of the 3 main trigonometric ratios in a right triangle.
In a right triangle (sometimes called a right-angled triangle), the tangent of an angle |(\boldsymbol \theta)| corresponds to the ratio of the measure of the side opposite the angle to the adjacent side (or leg).
||\tan \theta=\dfrac{\text{The side $\color{#EC0000}{\text{opposite}}$ angle }\theta}{\text{The side $\color{#333FB1}{\text{adjacent}}$ to angle }\theta}||
So, to find the tangent of the two acute angles in the following right triangle, we get the following 2 ratios.
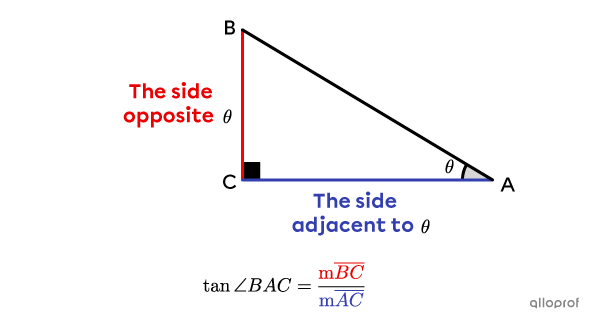
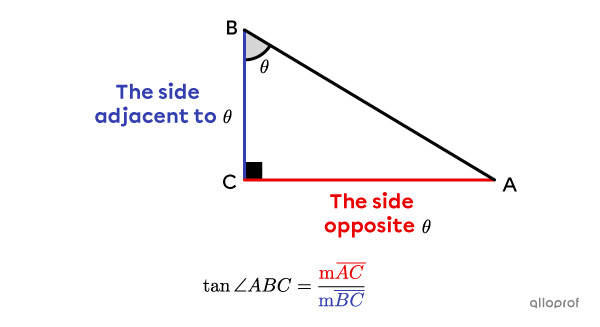
The tangent ratio is only used with acute angles. Never use the tangent ratio with a right angle.
Finding the Measurement of a Side Using the |\boldsymbol\tan| Ratio
The tangent ratio makes it possible to determine the measure of one of the 2 legs of a right triangle using the measure of an acute angle and the other leg.
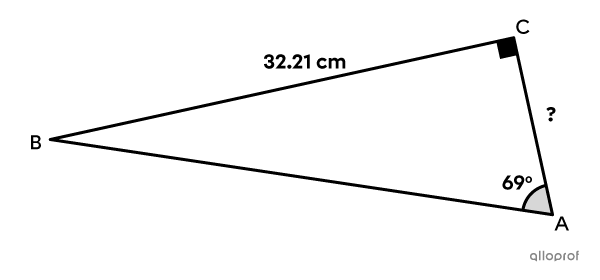
Find the measure of the side |\overline{BC}| using the tangent ratio in the following triangle.
See solution
To ensure accuracy, it is best to calculate (on the calculator) in one step. If it is not possible, round to at least 3 or 4 decimal places during each step.
For example, when |\theta=65^{\circ}| and its adjacent side is |59\ \text{cm},| we obtain the following.
Calculating in 1 Step
|\begin{align}\tan65^{\circ}&=\dfrac{a}{{59}}\\\tan65^{\circ}\times59&=a\\\color{#EC0000}{126.53}&\approx a\end{align}|
Calculating in 2 Steps
|\begin{align}\tan65^{\circ}&=\dfrac{a}{59}\\\color{#ec0000}{2.14}&\approx\dfrac{a}{59}\\2.14\times59&\approx a\\\color{#EC0000}{126.26}&\approx a\end{align}|
By calculating in 2 steps and keeping only 2 decimal places when calculating the tangent of the angle, the answer is 27 hundredths off from the correct response.
Determine the measure of the unknown side using the tangent ratio in the following right triangle.
See solution
Finding the Measurement of an Angle Using the |\boldsymbol\tan^{-1}| Ratio
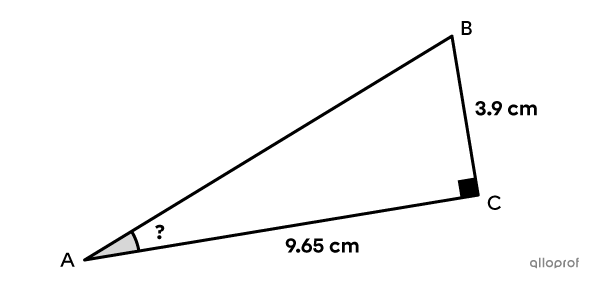
To find the measure of an acute angle in a right triangle using the tangent ratio, the measures of the legs opposite and adjacent the angle are required. This is the equivalent of asking: “Which angle creates a tangent ratio of…?”
We first find the tangent ratio and then press the |\tan^{-1}| (|arctan|) button on the calculator.
Using the tangent ratio, find the measure of angle |BAC| in the right triangle below.
See solution
The arc tangent function (denoted as |\tan^{-1}(x)|) is the inverse of the tangent function.
||\tan \theta=x\ \Leftrightarrow \ \tan^{-1}x=\theta||