The Zeroes of a Trigonometric Function

Do not forget that a trigonometric function is periodic. Therefore, it is necessary to check the interval of the function that is worked on in order to find all of the values sought.

1. Determine the period of the function using the formula |P=\dfrac{2\pi}{\vert b\vert}.|

2. Solve the equation |f(x)=0.|
   
   Isolate the expression |\sin\big(b(x-h)\big).|
   
   Look for the angle or angles which have this value of the sine. It is important to refer to the unit circle to see if it is a special point; if not, use the arcsin function on a calculator.
   
   Isolate |x| since each of the preceding angles is equal to the expression |b(x-h).|

3. Provide the solution set while taking into account the period of the function.

Consider the function |f(x)=-2\sin\left(\dfrac{1}{2}(x-1)\right)+1.|

1. Determine the period of the function:
   ||P=\dfrac{2\pi}{\vert b\vert}=\dfrac{2\pi}{\left\vert\frac{1}{2}\right\vert}=4\pi.||

2. Solve the equation |f(x)=0|
   |\begin{eqnarray*} 0 &=& -2\sin(\frac{1}{2}(x-1))+1 \\
   -1 &=& -2\sin(\frac{1}{2}(x-1)) \\
   \frac{1}{2} &=& \sin(\frac{1}{2}(x-1)) \end{eqnarray*}|
   
   At this stage, look in the unit circle for the values of the sine (y) which are equal to |\dfrac{1}{2}.| We are referring to the unit circle since |\dfrac{1}{2}| is a special point of sine within the unit circle.
   
   There are two places where sine has the value |\dfrac{1}{2}|: at |\dfrac{\pi}{6}| radians and |\dfrac{5\pi}{6}| radians.
   
   These two values are then set equal to |\frac{1}{2}(x-1)|.
   
   All that remains is to isolate |x|.
   |\begin{eqnarray*}
   \frac{\pi}{6}&=& \frac{1}{2}(x-1) \\
   2 \times \frac{\pi}{6} &=& x-1 \\
   \frac{\pi}{3} &=& x -1 \\
   \frac{\pi}{3} + 1 &=& x \end{eqnarray*}|
   and
   |\begin{eqnarray*}
   \frac{5\pi}{6} &=& \frac{1}{2}(x-1) \\
   2 \times \frac{5\pi}{6} &=& x -1 \\
   \frac{5\pi}{3} &=& x - 1 \\
   \frac{5\pi}{3} + 1 &=& x \end{eqnarray*}|

3. The two zeroes are therefore |\dfrac{\pi}{3}+1| radians and |\dfrac{5\pi}{6}+1| radians. Lastly, give the solution set by taking into account the period of the function.
   
   Zeroes of |f|: |\left\{\dfrac{\pi}{3}+1+4\pi n\right\}\cup\left\{\dfrac{5\pi}{6}+1+4\pi n\right\}\ \text{where}\ n\in\mathbb{Z}.|

Consider the function |f(x)=4\sin(-2x)+3|.

1. Determine the period of the function:
   ||P=\dfrac{2\pi}{\vert b\vert}=\dfrac{2\pi}{\vert -2\vert}=\pi||

2. Solve the equation |f(x)=0|.

|\begin{eqnarray*}
0 &=& 4\sin(-2x) + 3 \\
-3 &=& 4 \sin(-2x) \\
-\frac{3}{4} &=& \sin(-2x) \end{eqnarray*}|

At this step, use a calculator since the value |-\dfrac{3}{4}| is not a special point on the unit circle.
|\sin^{-1}\left(-\frac{3}{4}\right)\approx-0.848| radian is obtained.
Transform this negative value into a positive by adding |2\pi| (one full rotation). |-0.848+2\pi=5.435| radians.

Use a unit circle to obtain the second value.

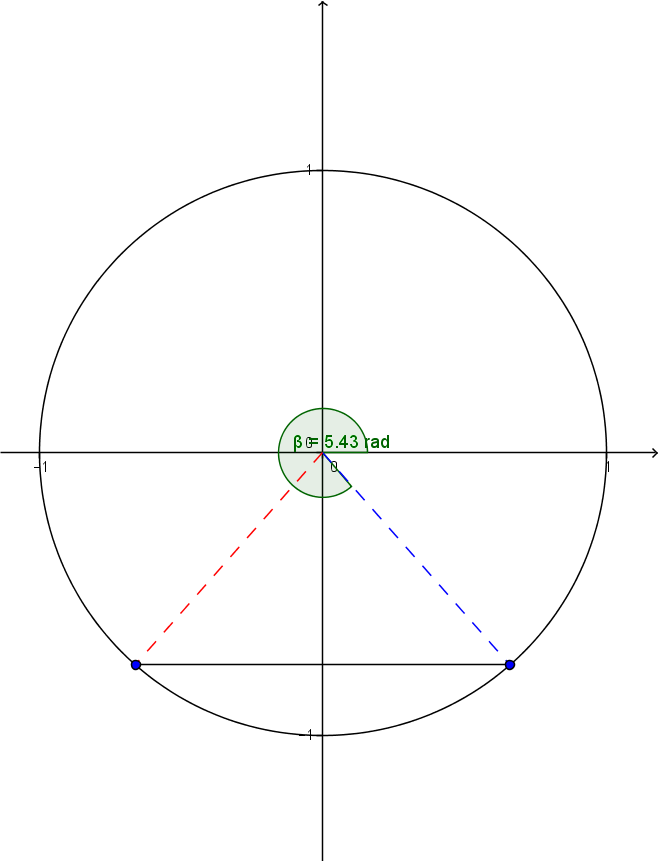
The angle already obtained is shown in green. Now we’re looking for the angle formed by the positive |x|-axis and the dotted segment in red.
Next, proceed as follows:
|2\pi - 5.435 + \pi \approx 3.99| radians

These two values are thus equal to |-2x|.

|5.435 = -2x \Rightarrow x = -2.7175|
and
|3.99 = -2x \Rightarrow x = -1.995|

3. The two zeroes equal |-2.7175| radians and |-1.995| radians.
   Lastly, give the solution set by taking into account the period of the function.
   Zeroes of |f|: |\{-2.7175+\pi n\}\cup\{-1.995+\pi n\}\ \text{where}\ n\in\mathbb{Z}.|

While searching for the zeroes of a sine function, at the step for isolating |\sin\big(b(x-h)\big),| it is absolutely necessary that |-1\le\sin\big(b(x-h)\big)\le1.| If not, the function does not have any zeroes. Indeed, the values of sine are between |-1| and |1| inclusively.

1. Determine the period of the function using the formula |P=\dfrac{2\pi}{\vert b\vert}.|

2. Solve the equation |f(x)=0.|
   
   Isolate the expression |\cos\big(b(x-h)\big).|
   
   Look for the angle(s) which have the value of the cosine. Refer to the unit circle to see if the value is a special point, otherwise use a calculator with the arccosine function.
   
   Isolate |x| since each of the preceding angles is equal to the expression |b(x-h).|

3. Provide the solution set, taking into account the period of the function.

Consider the function |f(x)=-2\cos\left(\dfrac{1}{2}(x-1)\right)+1.|

1. Determine the period of the function:
   ||P=\dfrac{2\pi}{\vert b\vert}=\dfrac{2\pi}{\left\vert\frac{1}{2}\right\vert}=4\pi||

2. Solve the equation |f(x)=0|
   |\begin{eqnarray*} 0 &=& -2\cos(\frac{1}{2}(x-1))+1 \\
   -1 &=& -2\cos(\frac{1}{2}(x-1)) \\
   \frac{1}{2} &=& \cos(\frac{1}{2}(x-1)) \end{eqnarray*}|
   
   At this stage, look in the unit circle for the values of the cosine (x) which are equal to |\dfrac{1}{2}.| We are referring to the unit circle since |\dfrac{1}{2}| is a special point of cosine on the unit circle.
   
   There are two places where the cosine is |\dfrac{1}{2}|: at |\dfrac{\pi}{3}| radian and |\dfrac{5\pi}{3}| radians.
   
   These two values are equal to |\dfrac{1}{2}(x-1).|
   
   All that remains is to isolate |x.|
   |\begin{eqnarray*}
   \frac{\pi}{3}&=& \frac{1}{2}(x-1) \\
   2 \times \frac{\pi}{3} &=& x-1 \\
   \frac{2\pi}{3} &=& x -1 \\
   \frac{2\pi}{3} + 1 &=& x \end{eqnarray*}|
   and
   |\begin{eqnarray*}
   \frac{5\pi}{3} &=& \frac{1}{2}(x-1) \\
   2 \times \frac{5\pi}{3} &=& x -1 \\
   \frac{10\pi}{3} &=& x - 1 \\
   \frac{10\pi}{3} + 1 &=& x \end{eqnarray*}|

3. The two zeroes are |\dfrac{2\pi}{3}+1| radians and |\dfrac{10\pi}{3}+1| radians.
   Lastly, give the solution set by taking into account the period of the function.
   Zeroes of |f|: |\left\{\dfrac{2\pi}{3}+1+4\pi n\right\}\cup\left\{\dfrac{10\pi}{3}+1+4\pi n\right\}\ \text{where}\ n\in\mathbb{Z}.|

Consider the function |f(x)=4\cos(-2x)+3.|

1. Determine the period of the function: The period of the function is: |P=\dfrac{2\pi}{\vert b\vert}=\dfrac{2\pi}{\vert -2\vert}=\pi.|

2. Solve the equation |f(x)=0|

|\begin{eqnarray*}
0 &=& 4\cos(-2x) + 3 \\
-3 &=& 4 \cos(-2x) \\
-\frac{3}{4} &=& \cos(-2x) \end{eqnarray*}|

At this step, use the calculator since the value of |-\dfrac{3}{4}| is not a special point on the unit circle.
We obtain |\cos^{-1}\left(-\dfrac{3}{4}\right)\approx 2.419| radians.

To find the second value, refer to the unit circle.

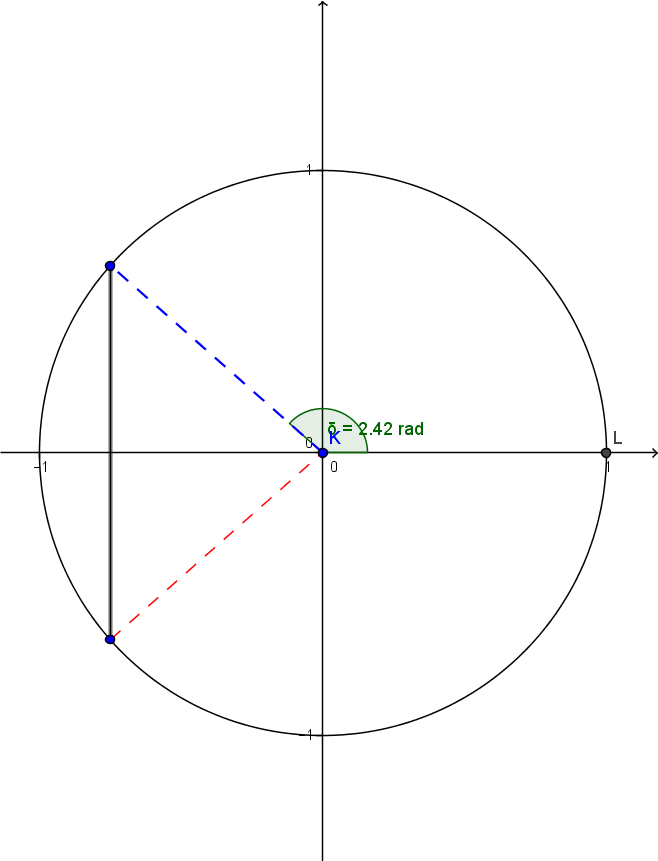
The angle already obtained is indicated in green. Now we’re looking for the angle formed by the positive |x|-axis and the dotted segment in red.
We proceed as follows:
|2\pi-2.419\approx3.864| radians

These two values are therefore equal to |-2x.|

|2.419 = -2x \Rightarrow x = -1.2095|
and
|3.864 = -2x \Rightarrow x = -1.932|

3. Thus, the two zeroes are |-1.2095| radians and |-1.932| radians.
   Lastly, give the solution set by taking into account the period of the function.
   Zeroes of |f| : |\{-1.2095+\pi n\}\cup\{-1.932+\pi n\}\ \text{where}\ n\in\mathbb{Z}.|

When searching for the zeroes of a cosine function, at the step where we isolate |\cos\big(b(x-h)\big),| it is absolutely necessary that |-1\le\cos\big(b(x-h)\big)\le1.| If not, the function does not have any zeroes. Indeed, the values of cosine are between -1 and 1 inclusively.

1. Determine the period of the function using the formula |P=\dfrac{\pi}{\vert b\vert}.|

2. Solve the equation |f(x)=0.|
   
   Isolate the expression |\tan\big(b(x-h)\big).|
   
   Look for the angle which has the value of the tangent. It is necessary to look in the unit circle to check if the value is a special point; if not, use a calculator with the arctangent function.
   
   Isolate |x| since the previous angle is equal to the expression |b(x-h).|

3. Give the solution set, taking into account the period of the function.

Consider the function |f(x)=2\tan\left(\dfrac{1}{3}(x-4)\right)+3.|

1. Determine the period of the function: ||P=\dfrac{\pi}{\vert b\vert}=\dfrac{2\pi}{\left\vert\frac{1}{3}\right\vert}=3\pi||

2. Solve the equation |f(x)=0|
   |\begin{eqnarray*} 0 &=& 2\tan(\frac{1}{3}(x-4))+3 \\
   -3 &=& 2\tan(\frac{1}{3}(x-4)) \\
   -\frac{3}{2} &=& \tan(\frac{1}{3}(x-4)) \end{eqnarray*}|

   At this step, find in the unit circle where the value of the tangent is equal to |-\dfrac{3}{2}.| Unfortunately, this value is not a special point. It is thus necessary to use the |\arctan| function on a calculator.
   
   |\tan^{-1}\left(-\dfrac{3}{2}\right)\approx-0.983| radians
   
   This value is equivalent to |\dfrac{1}{3}(x-4).|
   
   The only step that remains is to isolate |x.|
   |\begin{eqnarray*}
   -0.983 &=& \frac{1}{3}(x-4) \\
   3 \times -0.983 &=& x-4 \\
   -2.949 &=& x -4 \\
   -2.949+ 4 &=& x \\
   1.051 &=& x \end{eqnarray*}|

3. The zero of the function is |1.051| radians.
   Lastly, give the solution set by taking into account the period of the function.
   Zeroes of |f|: |\{1.051+3\pi n\}\ \text{where}\ n\in\mathbb{Z}.|