Subjects
Grades
Gravitational Potential Energy and Kinetic Energy
Concept sheet | Science and Technology
Secondary
4
When an object starts moving, it transfers or transforms its energy. For example, it can convert its potential energy into kinetic energy or vice versa.
Even when transformed, the total energy of an object is constant throughout its motion. The law of conservation of energy applies at all times, regardless of the motion.
Mechanical energy is the sum of potential energy and kinetic energy. The concept of mechanical energy is introduced in Secondary 5 Physics.
Gravitational Potential Energy
-
Potential energy is the energy stored by an object based on its position or shape.
-
Gravitational potential energy |(E_{p})| is the energy stored by an object according to its position relative to the ground.
The gravitational potential energy of an object varies proportionally based on:
-
its mass;
-
its height from the ground;
-
the gravitational field intensity of the celestial body to which it is attracted.
A watermelon and an apple sit on a table. The watermelon has greater gravitational potential energy than the apple, because the watermelon’s mass is greater.
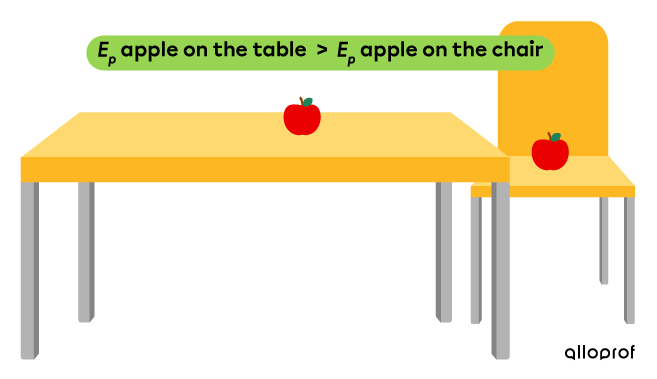
One apple sits on a table and another apple sits on a chair further down. The gravitational potential energy of the apple on the table is greater than the one on the chair, because its height relative to the ground is greater on the table.
To calculate the gravitational potential energy, we use the following formula.
|E_{p}=mgh|
where
|E_{p}| is the gravitational potential energy in Joules |(\text{J})|
|m| is the mass in kilograms |(\text{kg})|
|g| is the gravitational field strength in Newtons per kilogram |(\text{N/kg})|
|g_{Earth}=9.81\ \text{N/kg}|
|h| is the height relative to the ground in metres |(\text{m})|
-
Do not forget to convert the unit of mass to |\text{kg}| when necessary. In this case, we use the following conversion.
||1\ \text{kg} = 1\ 000\ \text{g}||
E.g.: |500\ \cancel{\text{g}} \times \dfrac{1\ \text{kg}}{1\ 000\ \cancel{\text{g}}} = 0.500\ \text{kg}| -
We generally use the value of the Earth’s gravitational field intensity |(g),| which is |9.81\ \text{N/kg}.| If the situation takes place on another celestial body, we use the value of |g| of the celestial body.
-
Some textbooks use the variable |\Delta y| instead of |h|. The variable |\Delta y| then represents a variation of the vertical position (along the |y|-axis |y|) relative to a reference point. We may opt for |\Delta y| when the reference point is not the ground |(0\ \text{m}).| In this case, the following formula will be used.
||\Delta y = y_{\text{f}}-y_{\text{i}}||
where
|y_{\text{f}}| is the final position along the the |y|-axis
|y_{\text{i}}| is the initial position along the |y|-axis
On October 14, 2012, Felix Baumgartner, a skydiver and extreme jumper, was launched from a helium balloon into the stratosphere to an altitude of |38\ 969\ \text{m}.|
It is estimated that Felix Baumgartner had a mass of |65.0\ \text{kg}.| What was his gravitational potential energy just before jumping?
The Stratos capsule
Red Bull designed the Stratos helium balloon attached to a capsule that carried Felix Baumgartner to the stratosphere before his jump.
Zinemo, Shutterstock.com
See solution
Kinetic Energy
Kinetic energy |(E_k)| is the energy an object possesses due to its motion.
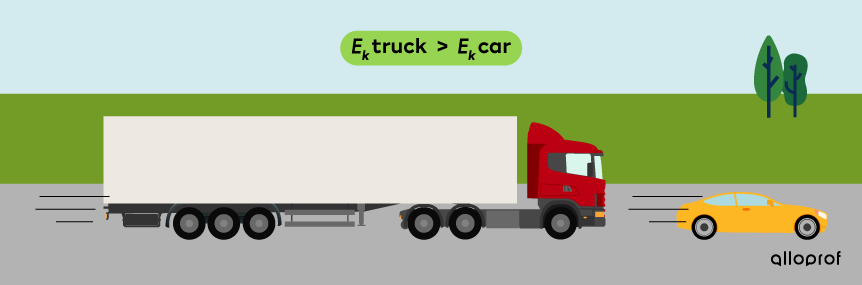
A truck and a car travel at the same speed. The kinetic energy of the truck is greater than the car’s, because its mass is greater.
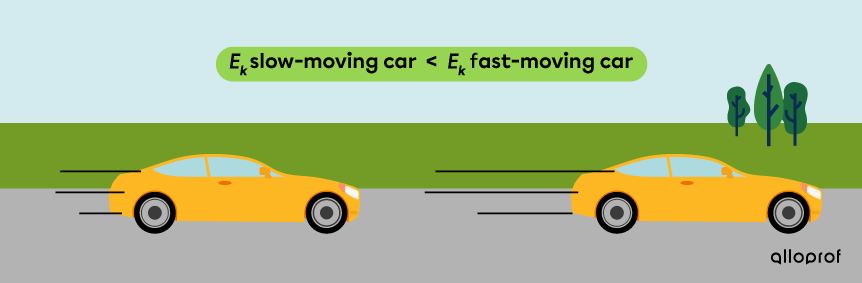
Two identical cars drive at different speeds. The kinetic energy of the fast-moving car is greater than the slow-moving car’s, because its speed is greater.
To calculate kinetic energy, use the following formula.
|E_k = \dfrac{1}{2}mv^2|
where
|E_k| is the kinetic energy in joules |(\text{J})|
|m| is the mass in kilograms |(\text{kg})|
|v| is the speed in metres per second |(\text{m/s})|
-
Do not forget to convert the mass unit when necessary. In this case, we use the following conversion.
||1\ \text{kg}= 1\ 000\ \text{g}||
E.g.: |500\ \cancel{\text{g}} \times \dfrac{1\ \text{kg}}{1\ 000\ \cancel{\text{g}}} = 0.500\ \text{kg}| -
Don't forget to convert the unit of speed to |(\text{m/s})| when necessary. In this case, we use the following conversion.
||3.6\ \text{km/h}=1\ \text{m/s}||
because
||\dfrac {3.6\ \text{km}}{h}=\dfrac {1\ \cancel{\text{m}}}{\cancel{\text{s}}} \times\dfrac{3\ 600\ \cancel{\text{s}}}{\text{h}} \times \dfrac{1\ \text{km}}{1\ 000\ \cancel{\text{m}}}||
E.g.: |100\ \cancel{\text{km/h}} \times \dfrac{1\ \text{m/s}}{3.6\ \cancel{\text{km/h}}}=27.8\ \text{m/s}|
When Felix Baumgartner jumped from the stratosphere, he reached a maximum speed of |1\ 342\ \text{km/h}.|
If Felix Baumgartner’s estimated mass was |65.0\ \text{kg},| what was his kinetic energy when he reached maximum speed?
See solution
Transformation of Energy During a Pendulum’s Motion
According to the law of conservation of energy, energy can only be transferred or transformed. In our daily lives, several phenomena make it possible to observe and verify the law. In a free fall motion or in an oscillating motion, the potential energy of an object is gradually transformed into kinetic energy or vice versa. So, the object does not lose any energy.
In the following examples, the height and speed of the objects vary. The variation causes the potential energy of the object (relative to its height) to be converted into kinetic energy (relative to its speed). The transformation takes place alternately, because the energy is always conserved, so it is simply transformed.
The pendulum of a clock
Mulevich, Shutterstock.com
A tennis ball bouncing
Raul Jichici, Shutterstock.com
A skateboarder on a halfpipe
Nick_p1cn1c, Shutterstock.com
A gymnast on a high bar
Alex Kravtsov, Shutterstock.com
Analysis of a pendulum’s energy transformation
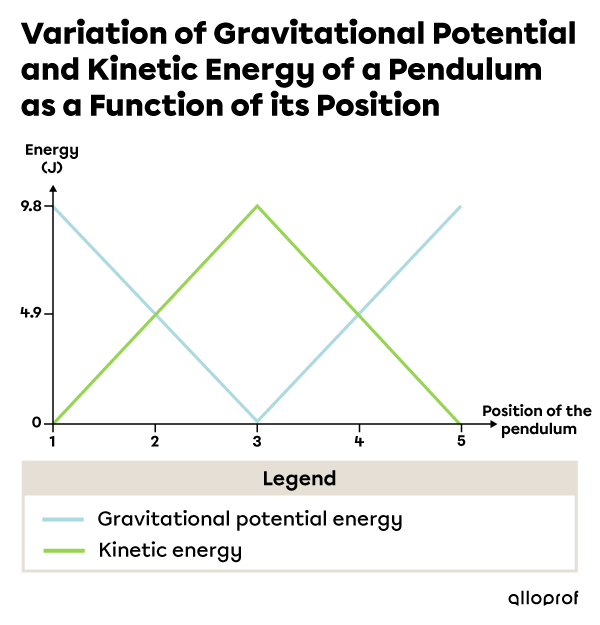
The |1.0\ \text{kg}| pendulum’s motion demonstrates the change in gravitational potential and kinetic energy as the pendulum's position and speed change.
The pendulum is stationary at position 1, at a height of |1.0\ \text{m}| relative to the ground. Next, the pendulum falls through positions 2 and 3. Finally, it rises to reach positions 4 and 5.
If we consider that the pendulum does not lose any energy, the back and forth motion goes on continuously because the total energy of the pendulum is conserved.
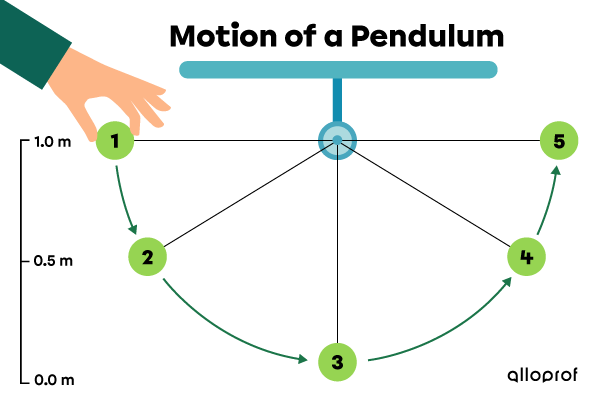
Motion of a pendulum
|
Variation of the Gravitational Potential and Kinetic Energy of a Pendulum According to its Position |
||||
|
Position |
Height |(\text{m})| |
Gravitational potential energy |(\text{J})| |
Speed |(\text{m/s})| |
Kinetic energy |(\text{J})| |
|---|---|---|---|---|
| 1 | |1.0| | |9.8| | |0.0| | |0.0| |
| 2 | |0.5| | |4.9| | |3.13| | |4.9| |
| 3 | |0.0| | |0.0| | |4.43| | |9.8| |
| 4 | |0.5| | |4.9| | |3.13| | |4.9| |
| 5 | |1.0| | |9.8| | |0.0| | |0.0| |
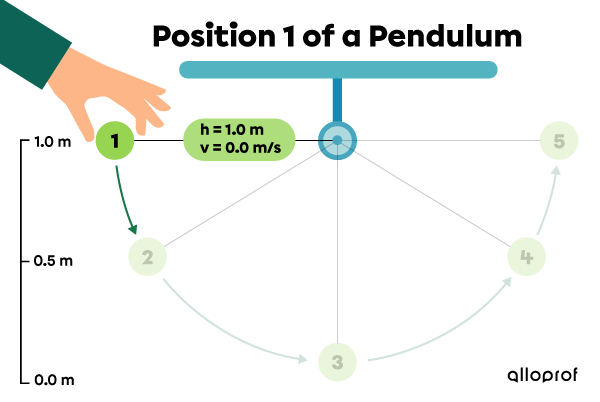
Position 1: the pendulum is stationary at its maximum height.
|\begin{align} E_{p}&=mgh\\
E_{p}&=1.0\ \cancel{\text{kg}}\times 9.8\ \text{N/}\cancel{\text{kg}} \times 1.0\ \text{m}\\
E_{p}&=9.8\ \text{J}\end{align}|
|\begin{align} E_k&=\dfrac{1}{2}mv^2\\
E_k&=\dfrac{1}{2} \times 1.0 \text{kg}\times (0.0\ \text{m/s})^2\\
E_k&=0.0\ \text{J}\end{align}|
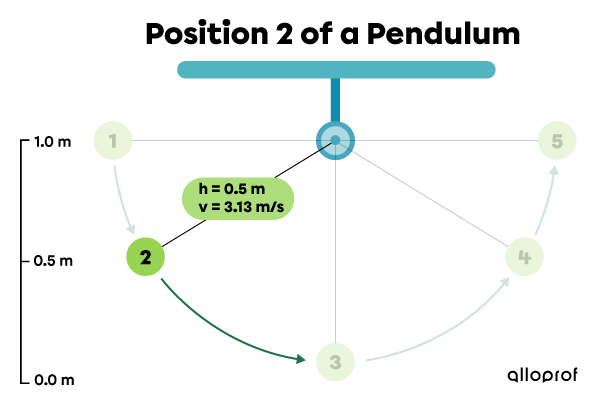
Position 2: the pendulum loses gravitational potential energy, but gains kinetic energy.
|\begin{align} E_{p}&=mgh\\
E_{p}&=1.0\ \cancel{\text{kg}}\times 9.8\ \text{N/}\cancel{\text{kg}} \times 0.5\ \text{m}\\
E_{p}&=4.9\ \text{J}\end{align}|
|\begin{align} E_k&=\dfrac{1}{2}mv^2\\
E_k&=\dfrac{1}{2} \times 1.0 \text{kg}\times (3.13\ \text{m/s})^2\\
E_k&=4.9\ \text{J}\end{align}|
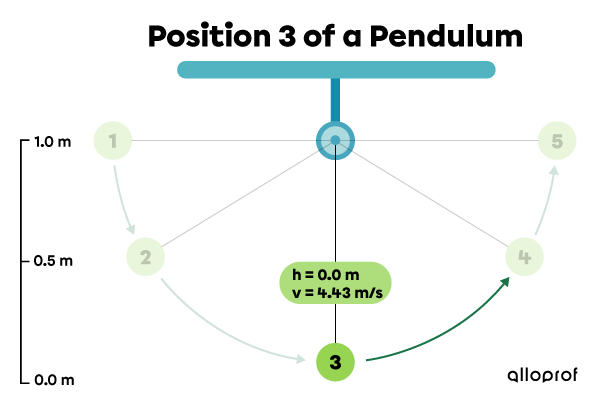
Position 3: the pendulum skims the ground and reaches its maximum speed.
|\begin{align} E_{p}&=mgh\\
E_{p}&=1.0\ \cancel{\text{kg}}\times 9.8\ \text{N/}\cancel{\text{kg}} \times 0.0\ \text{m}\\
E_{p}&=0.0\ \text{J}\end{align}|
|\begin{align} E_k&=\dfrac{1}{2}mv^2\\
E_k&=\dfrac{1}{2} \times 1.0 \text{kg}\times (4.43\ \text{m/s})^2\\
E_k&=9.8\ \text{J}\end{align}|
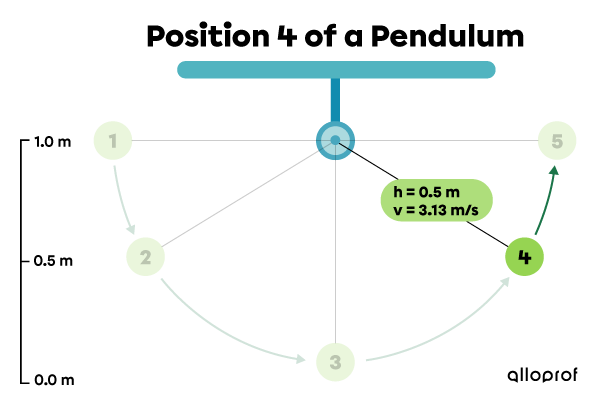
Position 4: The pendulum gains gravitational potential energy, but loses kinetic energy.
|\begin{align} E_{p}&=mgh\\
E_{p}&=1.0\ \cancel{\text{kg}}\times 9.8\ \text{N/}\cancel{\text{kg}} \times 0.5\ \text{m}\\
E_{p}&=4.9\ \text{J}\end{align}|
|\begin{align} E_k&=\dfrac{1}{2}mv^2\\
E_k&=\dfrac{1}{2} \times 1.0 \text{kg}\times (3.13\ \text{m/s})^2\\
E_k&=4.9\ \text{J}\end{align}|
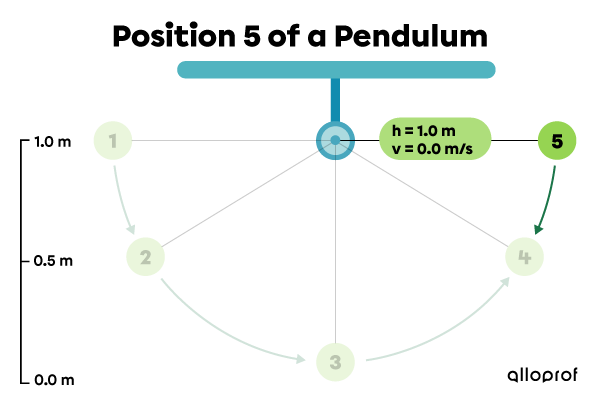
Position 5: the pendulum is stationary at its maximum height just before falling.
|\begin{align} E_{p}&=mgh\\
E_{p}&=1.0\ \cancel{\text{kg}}\times 9.8\ \text{N/}\cancel{\text{kg}} \times 1.0\ \text{m}\\
E_{p}&=9.8\ \text{J}\end{align}|
|\begin{align} E_k&=\dfrac{1}{2}mv^2\\
E_k&=\dfrac{1}{2} \times 1.0 \text{kg}\times (0.0\ \text{m/s})^2\\
E_k&=0.0\ \text{J}\end{align}|
Finally, the pendulum will fall back to positions 4, 3, 2, and 1 in a back and forth motion.
Exercise
Reference
Stanton, C. (January 22, 2021). Red Bull Stratos mission: The Inside Story of the Red Bull Stratos. Red Bull. https://www.redbull.com/ca-en/films/mission-to-the-edge-of-space