Subjects
Grades
Work, Effective Force and Displacement
Concept sheet | Science and Technology
Secondary
4
-
Work is a transfer of energy associated with the displacement of an object.
-
The effective force is the component of a force responsible for the displacement of an object.
-
Displacement is the distance from the starting point to the final point of an object.
Relationship Between Work, Effective Force, and Displacement
The work done on an object varies depending on the displacement of this object and the effective force applied to it:
-
the greater the displacement, the greater the work done on this object;
-
the greater the effective force, the greater the work done on the object.
By convention, the unit of measurement of work is the joule (|\text{J}|): 1 joule is the amount of energy needed to displace an object over a distance of 1 metre (|\text{m}|) using an effective force of 1 newton (|\text{N}|).
The following mathematical formula is used to calculate the work exerted on an object.
|W = F_{eff} \cdot \Delta s|
where
|W| represents work (|\text{J}|)
|F_{eff}| represents the effective force (|\text{N}|)
|\Delta s| represents the displacement of the object (|\text{m}|)
The effective force is the component of the applied force that is parallel to the displacement of an object. The effective force has the same direction as the displacement.
It can also be identified as “the force parallel to displacement”.
A crane lifts a beam over a distance of |20\ \text {m}| in height. To achieve this, the crane applies an upward constant tension of |1\ 000\ \text {N}|.
What is the work done by the crane to displace the beam?
See solution
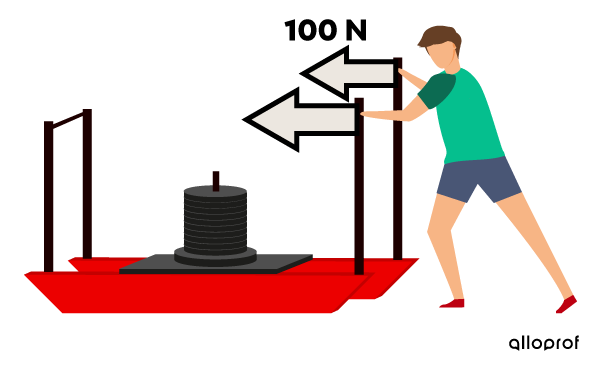
A person horizontally applies a force of |100\ \text{N}| on a trolley loaded with cast iron discs. Despite this effort, the trolley remains motionless.
How much work is the person doing on the trolley?
See solution
The calculation of work is obtained by a scalar product, that is the multiplication of two vectors. This involves a force vector and a displacement vector.
Furthermore, when the force applied to an object is not parallel to the displacement, the effective force must first be determined using a trigonometric ratio in a right-angled triangle before calculating the work.
A person pulls a box over a distance of |5\ \text{m}| by applying a force of |40\ \text {N}| at an angle of |30^\circ| relative to the horizontal.
What is the work performed by the person on the box?
See solution
Relationship Between Work and Energy
When we perform work, we use energy. According to the law of conservation of energy, energy is neither lost nor created, it is transferred or transformed. Thus, the work experienced by an object is equivalent to its change in energy.
The mathematical relationship between work and energy change is as follows:
|W=\Delta E|
where
|W| represents work |\text {(J)}|
|\Delta E| represents the change in energy (kinetic or potential) |\text {(J)}|
A person applies sufficient force to set a grocery cart in motion at a speed of |1{.}5\ \text {m/s}|.
The cart and its contents have a total mass of |15\ \text{kg}|.
What is the work performed by the person to displace the cart at a speed of |1{.}5\ \text{m/s}|?
