Matières
Niveaux
De la fraction au pourcentage et l'inverse
Fiche | Mathématiques
Secondaire
1-2
Dans certaines situations, il peut être utile de passer d'un pourcentage à une fraction ou l'inverse. La fiche suivante traite des méthodes à utiliser pour effectuer ces passages avec succès.
Exprimer une fraction en pourcentage
Il est possible d'exprimer une fraction sous la forme d'un pourcentage. Voici deux méthodes permettant d'y arriver.
Méthode 1
Cette méthode est plus efficace lorsque le dénominateur de la fraction de départ est un diviseur ou un multiple de |100|. Elle consiste à trouver une fraction équivalente dont le dénominateur est |100.|
-
Déterminer le nombre par lequel il faut multiplier ou diviser le dénominateur pour obtenir |100.|
-
Multiplier ou diviser le numérateur et le dénominateur de la fraction par ce nombre.
-
Écrire le numérateur de la fraction obtenu à l'étape 2 et ajouter le symbole % à droite de celui-ci.
Exprime la fraction |\displaystyle \frac{6}{25}| en pourcentage.
-
Déterminer le nombre par lequel il faut multiplier ou diviser le dénominateur pour obtenir |100.|
On détermine qu'on peut multiplier le dénominateur de la fraction par |\color{green}{4}| pour obtenir |100|.||25\times \color{green}{4}=100|| -
Multiplier ou diviser le numérateur et le dénominateur de la fraction par ce nombre.||\displaystyle \frac{6\times \color{green}{4}}{25\times \color{green}{4}}=\frac{24}{100}||
-
Écrire le numérateur de la fraction obtenu à l'étape 2 et ajouter le symbole % à droite de celui-ci.
La réponse est donc |24\ \%.|
Voici un autre exemple où l'on doit cette fois-ci utiliser la division pour obtenir un dénominateur de |100.|
Exprime la fraction |\dfrac{163}{200}| en pourcentage.
-
Déterminer le nombre par lequel il faut multiplier ou diviser le dénominateur pour obtenir |100.|
On détermine qu'on peut diviser le dénominateur de la fraction par |\color{green}{2}| pour obtenir |100|.||200\div \color{green}{2}=100|| -
Multiplier ou diviser le numérateur et le dénominateur de la fraction par ce nombre.||\displaystyle \frac{163\div \color{green}{2}}{200\div \color{green}{2}}=\frac{81{,}5}{100}||
-
Écrire le numérateur de la fraction obtenu à l'étape 2 et ajouter le symbole % à droite de celui-ci.
La réponse est donc |81{,}5\ \%.|
Méthode 2
Quoiqu'un peu plus complexe que la première méthode, celle-ci est beaucoup plus polyvalente.
-
Diviser le numérateur par le dénominateur.
-
Multiplier le quotient obtenu à |100.|
-
Ajouter le symbole % à droite du résultat.
Écris la fraction |\dfrac{5}{8}| en pourcentage.
-
Diviser le numérateur par le dénominateur.
-
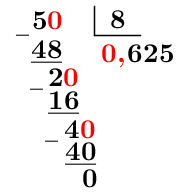
Multiplier le quotient obtenu à |100|.||0{,}625\times 100=62{,}5||
-
Ajouter le symbole % à droite du résultat.
|\dfrac{5}{8}| correspond donc à |62{,}5\ \%.|
Exprimer un pourcentage en fraction
Comme le pourcentage peut être vu comme une fraction dont le dénominateur est |100|, il est possible d'exprimer un pourcentage en fraction de la façon suivante.
-
Exprimer la pourcentage sous la forme d'une fraction dont le dénominateur est |100.|
-
Si le numérateur n'est pas un nombre entier, transformer celui-ci en nombre entier en multipliant le numérateur et le dénominateur par la puissance de |10| adéquate.
| Nombre de chiffres après la virgule | Puissance de |10| |
| |1| | |10| |
| |2| | |100| |
| |3| | |1\ 000| |
| ... | ... |
-
Au besoin, simplifier la fraction pour obtenir une fraction irréductible.
Il y a deux situations possibles : soit le pourcentage est un nombre entier, soit le pourcentage n'est pas un nombre entier. Voici un exemple pour chaque situation.
Exprime |28\ \%| sous la forme d'une fraction irréductible.
-
Exprimer le pourcentage sous la forme d'une fraction dont le dénominateur est |100.|||\dfrac{28}{100}||
-
Si le numérateur n'est pas un nombre entier, transformer celui-ci en nombre entier en multipliant le numérateur et le dénominateur par la puissance de |10| adéquate.
Comme le pourcentage est un nombre entier, on peut passer à l'étape 3. -
Au besoin, simplifier la fraction pour obtenir une fraction irréductible. ||\dfrac{28\color{green}{\div 4}}{100\color{green}{\div 4}}=\dfrac{7}{25}||
|28\ \%| correspond donc à la fraction irréductible |\dfrac{7}{25}.|
Voici un exemple où le pourcentage n'est pas un nombre entier.
Exprime |72{,}4\ \%| sous la forme d'une fraction irréductible.
-
Exprimer le pourcentage sous la forme d'une fraction dont le dénominateur est |100|.||72{,}4\ \%=\displaystyle \frac{72{,}4}{100}||
-
Si le numérateur n'est pas un nombre entier, transformer celui-ci en nombre entier en multipliant le numérateur et le dénominateur par la puissance de |10| adéquate.
Comme le numérateur possède un chiffre après la virgule, on devra multiplier le numérateur et le dénominateur par |10.| ||\dfrac{72{,}4\color{green}{\times 10}}{100\color{green}{\times 10}}=\dfrac{724}{1\ 000}|| -
Au besoin, simplifier la fraction pour obtenir une fraction irréductible.
On simplifie la fraction.||\dfrac{724\color{green}{\div 4}}{1\ 000\color{green}{\div 4}}=\dfrac{181}{250}|| |72{,}4\ \%| correspond donc à la fraction irréductible |\dfrac{181}{250}.|
Vidéos
