L'aire des triangles à l'aide de la formule de Héron

La formule de Héron est une formule qui permet de trouver l'aire d'un triangle quelconque à partir des mesures de ses trois côtés.

L'aire A d'un triangle quelconque, dont les mesures des côtés sont |a,| |b| et |c,| est donnée par la formule suivante : ||A=\sqrt{p(p-a)(p-b)(p-c)}||

où |p| représente le demi-périmètre du triangle, donné par la formule ci-dessous : ||p=\frac{a+b+c}{2}||

Calculons l'aire du triangle ci-dessous.

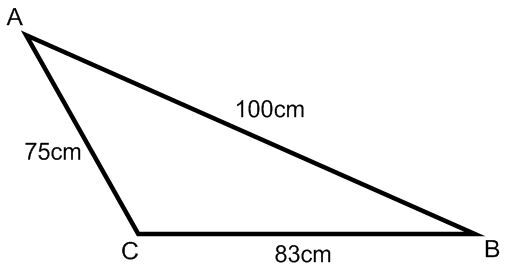
Calcul du demi-périmètre:
||\begin{align} p &=\frac{a+b+c}{2} \\\\
&=\frac{75+83+100}{2}\\\\
&=129\ \mathrm{cm}\\\\
\Rightarrow A&=\sqrt{p(p-a)(p-b)(p-c)}\\
&=\sqrt{129(129-75)(129-83)(129-100)}\\
&=3\ 048{,}38\ \mathrm{cm}^{2}\end{align}||
L'aire du triangle ABC est de |3\ 048{,}38\ \mathrm{cm}^2|.

Déterminez l'aire du triangle ci-dessous:

Il faut d'abord déterminer la mesure manquante pour le troisième côté du triangle. Pour ce faire, on peut utiliser la loi des sinus.
||\begin{align} \frac{a}{\sin A} &= \frac{b}{\sin B} &&= \frac{c}{\sin C}\\\\
\Rightarrow \frac{3}{\sin 25°} &= \frac{6{,}64}{\sin B} &&\\\\
\frac{6{,}64\times {\sin 25°}}{3} &= \sin B &&\\\\
0{,}9354 &\approx \sin B &&\\
69{,}29^\circ &\approx B && \end{align}||
Le troisième angle (angle C) est donc:
||180 - 25 - 69{,}29 = 85{,}71°||
On peut donc à nouveau utiliser la loi des sinus afin de déterminer la mesure du côté manquant.
||\begin{align} \frac{3}{\sin 25°} &= \frac{c}{\sin 85{,}71°}\\\\
\frac{\sin 85{,}71° \times {3}}{\sin 25°} &= c\\\\
7{,}08 &\approx c\end{align}||
Maintenant que l'on connait la mesure du côté manquant, on peut déterminer le demi-périmètre et trouver l'aire du triangle à l'aide de la formule de Héron.
||\begin{align} p&=\frac{a+b+c}{2}\\\\
&=\frac{3 + 6{,}64 + 7{,}08}{2}\\\\
&=8{,}36\ \mathrm{cm} \\\\
\Rightarrow A&=\sqrt{p(p-a)(p-b)(p-c)}\\
&=\sqrt{8{,}36(8{,}36-3)(8{,}36-6{,}64)(8{,}36-7{,}08)}\\
&=10\ \mathrm{ cm}^{2}\end{align}||
L'aire du triangle est de |10\ \mathrm{ cm}^2.|

Formule trigonométrique

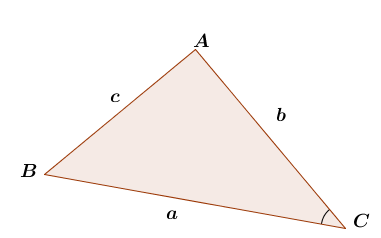
Il est aussi possible de calculer l'aire d'un triangle si on connait la mesure de deux de ses côtés ainsi que la mesure de l'angle compris entre ses côtés. On utilise alors la formule trigonométrique suivante : ||A = \frac{a\times b \times \sin C}{2}||