La composition de transformations géométriques dans un plan cartésien

​Lorsque l'on effectue plusieurs transformations géométriques successivement, la règle qui relie ces transformations est une composition et le résultat est appelé la composée. On utilise le symbole |\circ| que l'on lit «rond».

On effectue toujours les transformations d'une composition de droite à gauche.

Soit le triangle |ABC|. On veut effectuer la transformation |t_{(1,-2)} \circ r_{(O,90°)}|.

On effectue au départ une rotation de centre |O| (ici, c'est l'origine du plan cartésien) suivie d'une translation.

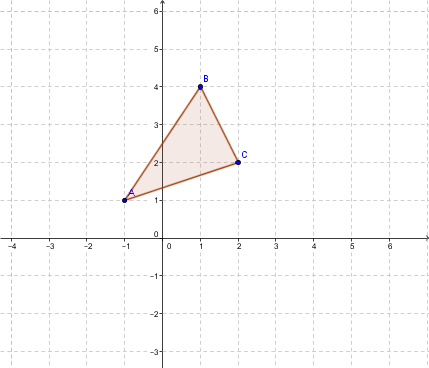
Les coordonnées des sommets du triangle |ABC| sont:
|A(-1,1)|;
|B(1,4)|;
|C(2,2)|.

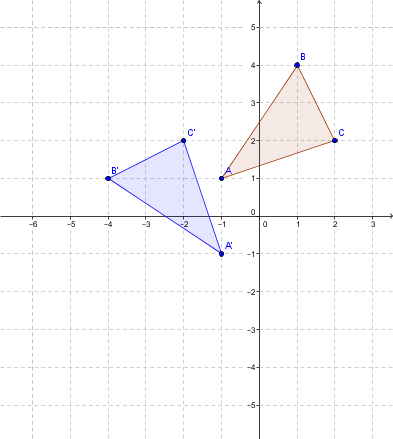
Étape 1: On effectue la rotation de centre |O| et d'angle de |90°| dans le sens antihoraire.

On utilise la règle |r_{(O,90°)}:(x,y) \mapsto (-y,x)|.

|A=(-1,1) \mapsto (-1,-1)=A'|;
|B=(1,4) \mapsto (-4,1)=B'|;
|C=(2,2 \mapsto (-2,2)=C'|.

On obtient alors le triangle bleu.

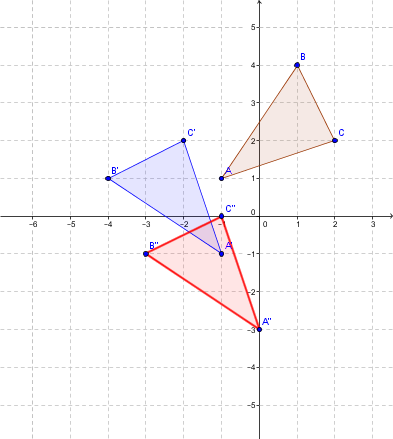
Étape 2: On doit maintenant effectuer la translation avec la règle |t_{(1,-2)}:(x,y) \mapsto (x+1,y-2)|.

On obtient alors les points:
|A'=(-1,-1) \mapsto (0,-3)=A''|;
|B'=(-4,1) \mapsto (-3,-1)=B''|;
|C'=(-2,2) \mapsto (-1,0)=C''|.

On obtient alors le triangle rouge qui est la figure image.