Matières
Niveaux
Le rôle des paramètres dans une fonction valeur absolue
Fiche | Mathématiques
Secondaire
5
Table des matières
- Haut de page
- Manipulation animée des paramètres
- L'analyse du paramètre |a|
- Un changement d'échelle vertical de la courbe de facteur |a|
- Une réflexion du graphique de la fonction autour de l'axe des |x|
- L'analyse du paramètre |b|
- Un changement d'échelle horizontal de la courbe de facteur |\dfrac{1}{b}|
- L'analyse du paramètre |h|
- Une translation horizontale de toute la fonction
- L'analyse du paramètre |k|
- Une translation verticale de toute la fonction
- À voir aussi
Lorsqu’on ajoute les paramètres |a,| |b,| |h| et |k| à la forme de base |f(x)={\mid}x{\mid}| on obtient ce qu'on appelle la forme canonique (aussi appelée forme transformée) de la fonction valeur absolue.
La forme canonique de la fonction valeur absolue est : ||f(x)=a {\mid}b(x-h){\mid} +\ k||où |a,| |b,| |h| et |k| sont des nombres réels jouant le rôle de paramètres.
Remarques : Les paramètres |a| et |b| sont toujours différents de zéro.
Le couple |(h,k)| correspond au sommet de la fonction.
Avec quelques manipulations, on obtient une équation avec trois paramètres |(a, h, k),| et ce, en appliquant la propriété suivante : |{\mid}x \times y{\mid} = {\mid}x{\mid} \times {\mid}y{\mid}.|
|f(x) = a {\mid}b(x-h){\mid} + k|
|f(x)= a {\mid}b{\mid} {\mid}x - h{\mid} + k|
|f(x) = \mathbb{a} {\mid}x - h{\mid} + k| où |\mathbb{a} = a {\mid}b{\mid}|
Attention! Dans la dernière forme, le |\mathbb{a}| correspond à une combinaison des paramètres |a| et |b.| Son effet est donc équivalent à l'effet conjugué des deux paramètres.
Manipulation animée des paramètres
Tu peux modifier les paramètres |\mathbb{a}|, |h| et |k| dans l'animation interactive qui suit pour voir leurs effets sur la fonction valeur absolue. Observe bien les modifications qui s'opèrent sur la courbe transformée (en noir) par rapport à la fonction de base (en bleu). Tu peux en profiter pour observer l'effet de la modification des paramètres sur les propriétés de la fonction. Par la suite, tu pourras poursuivre la lecture de la fiche pour avoir toutes les précisions sur chacun des paramètres.
Remarque : On utilise simplement l'équation |f(x)=\mathbb{a} {\mid}x - h{\mid} + k| puisque le paramètre |b| est superflu.
L'analyse du paramètre |a|
Un changement d'échelle vertical de la courbe de facteur |a|
Lorsque |{\mid}a{\mid} > 1 :|
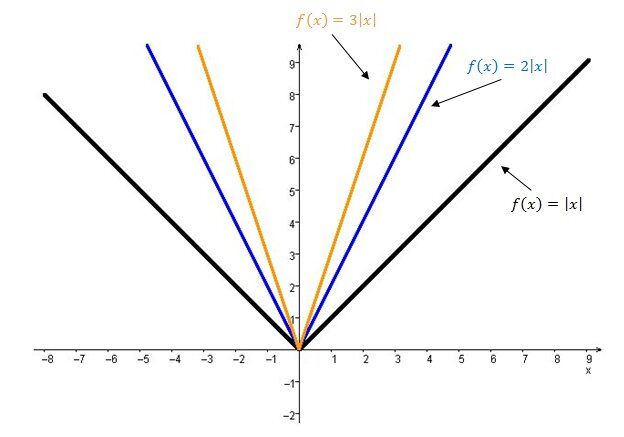
Plus la valeur absolue du paramètre |a| est grande, plus les branches du graphique de la fonction valeur absolue se rapprochent de l'axe des |y| parce que la courbe est étirée verticalement. On dirait que l'ouverture se referme.
Lorsque |0< {\mid}a{\mid} < 1 :|
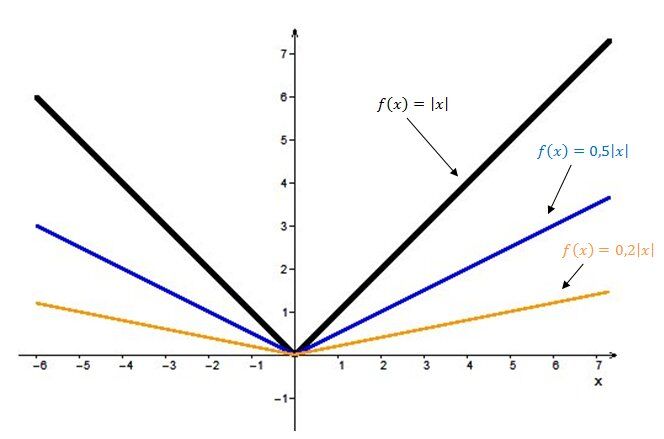
Plus le paramètre |a| est petit (près de 0), plus les branches du graphique de la fonction valeur absolue s'écrasent vers l'axe des |x.| On dirait que l'ouverture s'agrandit.
Une réflexion du graphique de la fonction autour de l'axe des |x|
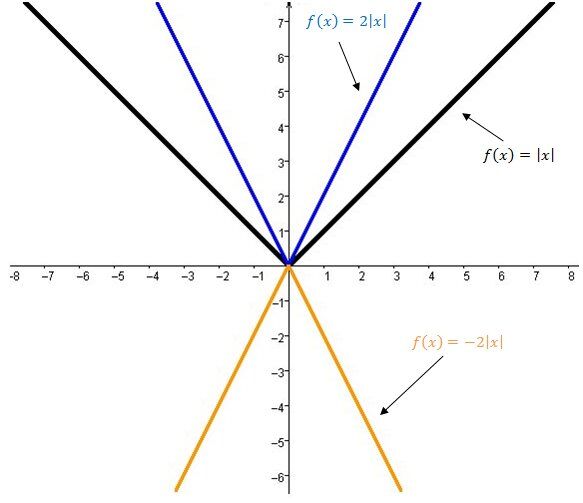
Le paramètre |a| est aussi responsable de l’orientation de la courbe de la fonction valeur absolue.
Lorsque |a| est positif |(a>0) :|
L’ouverture de la courbe de la fonction valeur absolue est dirigée vers le haut.
Lorsque |a| est négatif |(a<0) :|
L’ouverture de la courbe de la fonction valeur absolue est dirigée vers le bas.
L'analyse du paramètre |b|
Un changement d'échelle horizontal de la courbe de facteur |\dfrac{1}{b}|
Lorsque |{\mid}b{\mid} > 1 :|
Plus la valeur absolue du paramètre |b| est grande, plus l’ouverture de la courbe de la fonction valeur absolue est petite.
Lorsque |0< {\mid}b{\mid} < 1 :|
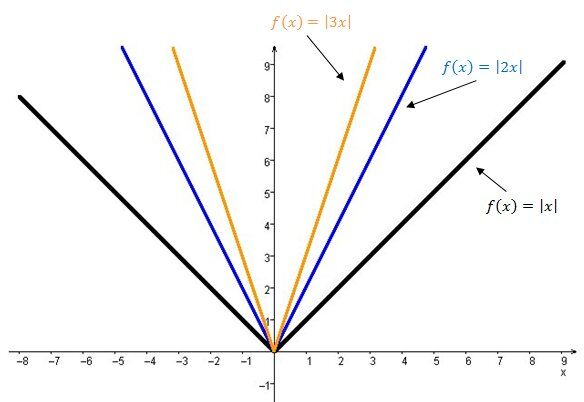
Plus le paramètre |b| est petit (près de 0), plus l’ouverture de la courbe de la fonction valeur absolue est grande.
L'analyse du paramètre |h|
Une translation horizontale de toute la fonction
Lorsque |h| est positif |(h>0) :|
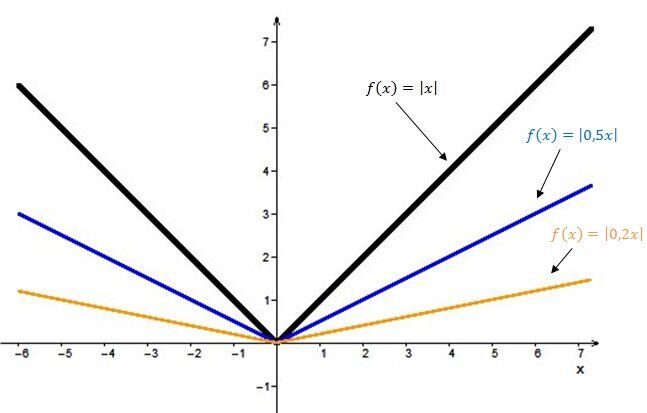
La courbe de la fonction valeur absolue se déplace vers la droite.
Lorsque |h| est négatif |(h<0) :|
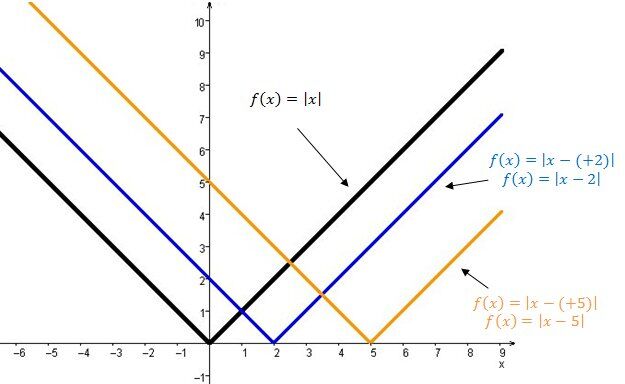
La courbe de la fonction valeur absolue se déplace vers la gauche.
L'analyse du paramètre |k|
Une translation verticale de toute la fonction
Lorsque |k| est positif |(k>0) :|
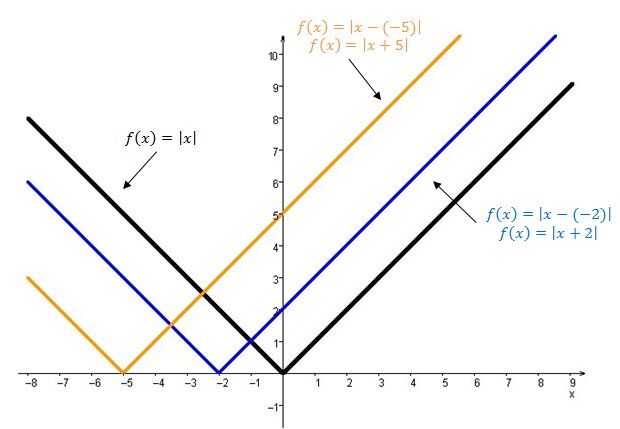
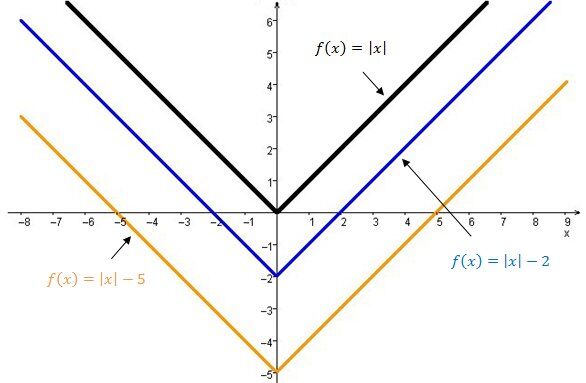
La courbe de la fonction valeur absolue se déplace vers le haut.
Lorsque |k| est négatif |(k<0) :|
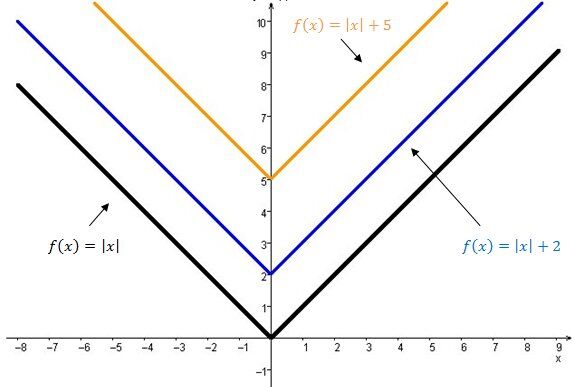
La courbe de la fonction valeur absolue se déplace vers le bas.
