Matières
Niveaux
Les méthodes de décomposition des figures
Fiche | Mathématiques
Secondaire
1-5
Table des matières
Dans certains cas, la figure géométrique utilisée pour représenter une situation ne possède pas de caractéristique particulière. Généralement, on peut découper cette figure afin de faire apparaitre des figures géométriques qui ont des propriétés particulières. Par la suite, il est plus facile d'en calculer son périmètre ou son aire.
Un polygone décomposable est un polygone que l'on peut séparer en plusieurs polygones plus simples.
Additionner les parties d'un tout
Afin de faciliter les calculs de périmètre et d'aire des figures décomposables, il est préférable d'utiliser des droites pour diviser la figure initiale. En fonction du contexte, il ne reste qu'à additionner les parties nécessaires pour obtenir la réponse.
Le polygone initial suivant :
peut être découpé de plusieurs façons :
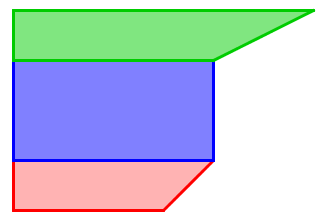
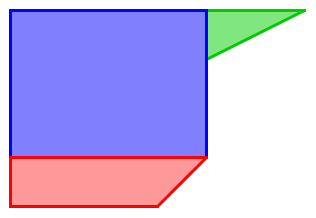
En fait, il est important de considérer les mesures de côté qui sont données afin de découper adéquatement le polygone initial. Par ailleurs, il est plus facile de découper un polygone en utilisant seulement des lignes droites qui ont comme point de départ un sommet du polygone initial.
Soustraire une partie d'un tout
Pour d'autres situations, on utilisera des figures géométriques reconnaissables (carré, triangle, trapèze, etc.) à l'intérieur desquelles on aura enlevé une partie.
Une fois que l'on garde en mémoire ces deux méthodes, il est plus facile de calculer l'aire et le périmètre de telles figures. Par ailleurs, la reconnaissance des figures utilisées dans chacun des dessins facilite la déduction de mesures manquantes.