Matières
Niveaux
Les modes de représentation d'une relation
Fiche | Mathématiques
Secondaire
1-2
Une relation est présente lorsqu'un lien existe entre deux variables. Généralement, on y retrouvera une variable indépendante qui influence une variable dépendante.
Il existe plusieurs façons de représenter une relation entre des variables :
Une relation peut être définie comme étant une fonction si, pour chaque valeur de la variable indépendante, il n'y a qu'une et une seule valeur de la variable dépendante. Si ce n'est pas le cas, la relation ne peut pas être qualifiée de fonction.
La description verbale
Une description verbale décrit de manière générale une fonction. Elle doit idéalement contenir 3 éléments :
- l'identification des variables;
- l'état initial de la situation;
- la description du comportement des variables l'une par rapport à l'autre.
On retrouve souvent des mots ou des expressions tels que en fonction de, dépend de, selon, etc. dans une description verbale.
Julien fait appel à un plombier pour l'aider à effectuer des travaux chez lui. Le tarif demandé est fonction du nombre d'heures travaillées. Le plombier demande |35\ \$| pour ses frais de déplacement et |50\ \$| pour chaque heure travaillée.
La table de valeurs
Une table de valeurs est un tableau qui comporte des couples de valeurs.
- Ces couples permettent de décrire numériquement une relation.
- Une table de valeurs peut être représentée horizontalement ou verticalement.
- La variable indépendante se trouve à la première rangée ou colonne de la table de valeurs et la variable dépendante se trouve dans la rangée ou colonne suivante.
Le cout d'un plombier en fonction du temps peut se représenter ainsi.
| Temps (h) | |0| | |1| | |2| | |3| | |4| | |5| | |...| |
|---|---|---|---|---|---|---|---|
| Tarif ($) | |35| | |85| | |135| | |185| | |235| | |285| | |...| |
Cette relation peut être qualifiée de fonction puisqu'il n'y a qu'une seule valeur de la variable dépendante (le tarif) pour chaque valeur de la variable indépendante (le temps).
Il peut arriver qu'une même valeur numérique se répète dans une table de valeurs.
| |\boldsymbol{x}| | |-5| | |-3| | |3| | |4| | |6| | |...| |
|---|---|---|---|---|---|---|
| |\boldsymbol{y}| | |0| | |\boldsymbol{\color{#ec0000}1}| | |\boldsymbol{\color{#ec0000}1}| | |17| | |8| | |...| |
Si la variable indépendante |(x)| se répète, la relation ne peut pas être qualifiée de fonction.
| |\boldsymbol{x}| | |\boldsymbol{\color{#ec0000}5}| | |\boldsymbol{\color{#ec0000}5}| | |\boldsymbol{\color{#ec0000}5}| | |\boldsymbol{\color{#ec0000}5}| | |\boldsymbol{\color{#ec0000}5}| | |...| |
|---|---|---|---|---|---|---|
| |\boldsymbol{y}| | |0| | |1| | |2| | |3| | |4| | |...| |
Le graphe
Le graphe permet de donner l'ensemble des solutions possibles pour une relation |(R)| entre deux variables. Ainsi, le graphe est l'extension de l'ensemble-solution, c'est-à-dire qu'il implique l'énumération des couples de solution possibles.
Le cout d'un plombier en fonction du temps peut s'écrire ainsi. ||R = \{(0,35), (1,85), (2,135), (3,185), (4,235), ...\}||Cette relation peut être qualifiée de fonction puisqu'il n'y a qu'une seule valeur de la variable dépendante (le tarif) pour chaque valeur de la variable indépendante (le temps).
Il peut arriver qu'une même valeur numérique se répète dans un graphe.
Si la variable dépendante |(y)| se répète, la relation peut être qualifiée de fonction.||R = \{(-5,0), (-3,\color{#ec0000}{1}), (3,\color{#ec0000}{1}), (4,17), (6,8)\}||
Si la variable indépendante |(x)| se répète, la relation ne peut pas être qualifiée de fonction.
||R = \{(\color{#ec0000}{5},0), (\color{#ec0000}{5},1), (\color{#ec0000}{5},2), (\color{#ec0000}{5},3), (\color{#ec0000}{5},4)\}||
Le graphique sagittal
Le graphique sagittal permet de représenter visuellement la relation existant entre deux variables.
- Un ensemble de départ A contient les valeurs de la variable indépendante;
- Un ensemble d'arrivée B contient les valeurs de la variable dépendante;
- Des flèches associent chaque valeur de la variable indépendante à sa valeur correspondante de la variable dépendante.
Le cout d'un plombier en fonction du temps peut visuellement être représenté ainsi.
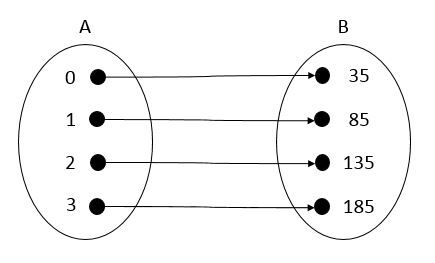
Cette relation peut être qualifiée de fonction puisqu'il n'y a qu'une seule valeur de la variable dépendante (le tarif) pour chaque valeur de la variable indépendante (le temps).
Il peut arriver qu'une même valeur numérique se répète dans un graphique sagittal.
Si la variable dépendante |(y)| se répète, la relation peut être qualifiée de fonction.
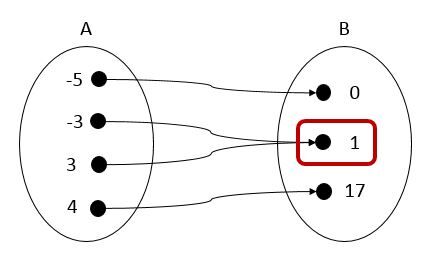
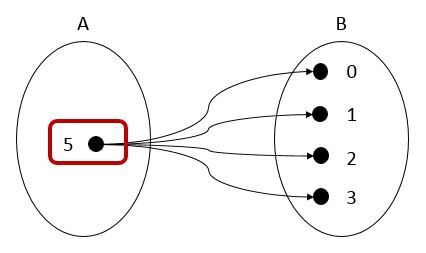
Si la variable indépendante |(x)| se répète, la relation ne peut pas être qualifiée de fonction.
Le plan cartésien
Le plan cartésien permet de représenter graphiquement le comportement d'une variable par rapport à une autre.
- La variable indépendante est associée à l'axe des abscisses (l'axe des |x|).
- La variable dépendante est associée à l'axe des ordonnées (l'axe des |y|).
- Le graphique peut comporter un nuage de points, une droite, une courbe ou un ensemble de courbe selon le type de relation qui y est représentée.
Le cout d'un plombier en fonction du temps peut se représenter graphiquement ainsi.
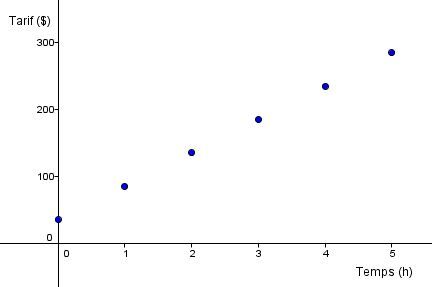
Cette relation peut être qualifiée de fonction puisqu'il n'y a qu'une seule valeur de la variable dépendante (le tarif) pour chaque valeur de la variable indépendante (le temps).
Il peut arriver qu'une même valeur numérique se répète dans le plan cartésien.
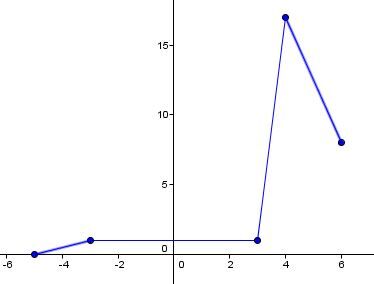
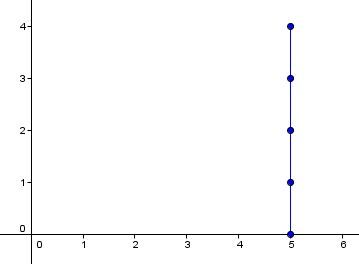
Si la variable dépendante |(y)| se répète, la relation peut être qualifiée de fonction (à gauche). Par contre, si c'est la variable indépendante |(x)| qui se répète, la relation ne peut pas être qualifiée de fonction (à droite).
La règle
Une règle implique une égalité qui traduit une relation de régularité entre des variables.
- La variable indépendante est notée |x.|
- La variable dépendante est notée |y.| Lorsqu'il s'agit d'une fonction, il est possible de la nommer |f(x).|
Les lettre utilisées pour nommer les variables peuvent toutefois changer.
Le cout d'un plombier en fonction du temps peut être désigné ainsi.
-
Le tarif en |$| est |y| ou |f(x).|
-
Le temps en heures est |x.|
La règle peut donc s'exprimer ainsi. ||y = 50x + 35||
Pour valider ta compréhension à propos des modes de représentation dans les situations de proportionnalité, les situations inversement proportionnelles et les suites arithmétiques, consulte la MiniRécup suivante.
