Matières
Niveaux
Les propriétés de la fonction affine
Fiche | Mathématiques
Secondaire
3-4
Table des matières
Dans l'animation suivante, tu peux modifier les paramètres |a| et |b| de la fonction polynomiale de degré 1 (fonction affine) et observer l'effet sur les propriétés de la fonction.
| Propriétés | Fonction affine sous la forme |y=ax+b| |
|---|---|
| Domaine |
|\mathbb{R}| ou selon le contexte |
| Image (codomaine) |
|\mathbb{R}| ou selon le contexte |
| Zéro de la fonction |
|\displaystyle x = \frac{-b}{a}| ou on remplace |y| par |0| puis on isole |x| |
| Signe de la fonction |
Si |a>0|, la fonction est négative sur |]-∞,\frac{-b}{a}]| et positive sur |[\frac{-b}{a},+∞[.| Si |a<0|, la fonction est positive sur |]-∞,\frac{-b}{a}]| et négative sur |[\frac{-b}{a},+∞[.| |
| Ordonnée à l'origine |
C'est la valeur de |b|. |
| Extrémums |
Aucun ou selon le contexte. |
| Croissance |
Si le taux de variation est positif |(a>0),| la fonction est croissante sur tout son domaine. |
| Décroissance |
Si le taux de variation est négatif |(a<0),| la fonction est décroissante sur tout son domaine. |
Déterminer les différentes propriétés de la fonction |y = 2x + 1|.
Il est très utile de tracer un graphique afin de s'aider à déterminer les propriétés.
-
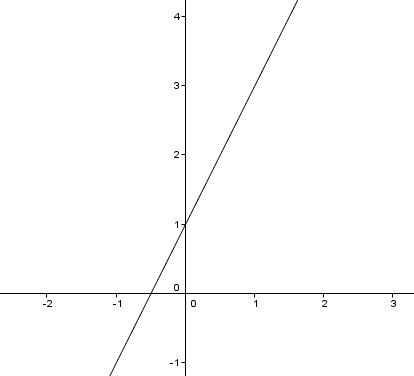
Le domaine de la fonction est l'ensemble des nombres réels que l'on note |\mathbb{R}| puisque la fonction n'est pas restreinte.
-
L'image de la fonction est l'ensemble des nombres réels que l'on note |\mathbb{R}| puisque la fonction n'est pas restreinte.
-
Le zéro de la fonction se calcule de la manière suivante: |\displaystyle x = \frac{-b}{a} = \frac{-1}{2}|. On peut aussi remplacer |y| par |0| puis isoler |x|. ||\begin{align} 0 &= 2x + 1 \\ -1 &= 2x \\ \displaystyle \frac{-1}{2} &= x \end{align}||
-
Le signe de la fonction est négatif de |]-∞,\frac{-1}{2}]| et positif de |[\frac{-1}{2},+∞[.|
-
L'ordonnée à l'origine est |b = 1.|
-
La fonction n'a aucun extrémum.
-
La fonction est croissante, car |a>0.|
Exercices
Pour valider ta compréhension des propriétés des fonctions de façon interactive, consulte la MiniRécup suivante :
