Matières
Niveaux
Il existe différentes façons d'exprimer l'ensemble-solution d'une inéquation.
La compréhension montre à la fois l'inéquation représentant la situation à l'étude ainsi que l'ensemble de nombres dans lequel cette inégalité se trouve.
Les nombres entiers supérieurs à -3 et inférieurs à 7. |\to\ \{x \in \mathbb{Z} \mid -3 < x < 7 \}|
Les nombres naturels supérieurs ou égaux à 2. |\to\ \{x \in \mathbb{N} \mid x \ge 2 \}|
Les nombres réels supérieurs ou égaux à -5 et inférieurs à 6. |\to\ \{x \in \mathbb{R} \mid -5 \le x < 6 \}|
Les inéquations à une variable peuvent être représentées sur une droite numérique.
Pour commencer, on représente la droite numérique et on positionne le nombre de notre inégalité.
Si le signe de l'inéquation contient une égalité |(\le, \ge)|, on place un point plein |(\bullet)| pour indiquer qu'on inclut ce point dans les solutions.
Si le signe de l'inéquation ne contient pas d'égalité |(<, >)|, on place un point vide |(\circ)| pour indiquer qu'on exclut ce point des solutions.
Exemple d'inéquation contenant une égalité
Soit l'inéquation suivante : ||\begin{align} 2x+5 &\le9 \\ 2x+5\color{red}{-5}&\le9\color{red}{-5} \\ 2x&\le4\\ \dfrac{2x}{\color{red}{2}} &\le\frac{4}{\color{red}{2}} \\ x &\le2 \end{align}||
Dans cet exemple, un point plein doit être indiqué sur le nombre 2 puisqu'une égalité est présente dans l'inéquation.
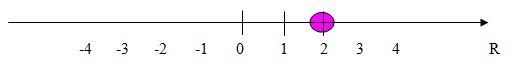
Il faut ensuite représenter l’inégalité de la solution de l'inéquation. Puisqu'il n'y a pas d'ensemble de nombres spécifié en début de problème, on considère que l'ensemble-solution fait partie des nombres réels. Il existe donc une infinité de solutions pour les inéquations.
Dans l’exemple, les solutions sont tous les nombres plus petits ou égaux à |2.| |2,| |1,| |\dfrac{1}{2},| |\dfrac{1}{4},| |0,| |-1,| |-2, …| sont donc des solutions de notre inéquation.
Pour représenter ceci, on fait une ligne pour indiquer toutes les valeurs solutions de l’inéquation.

Exemple d'inéquation ne contenant pas d'égalité
||\begin{align} 35-3x &< 7+4x \\ 35-3x \color{red}{+3x} &< 7+4x \color{red}{+3x} \\35 &<7+7x \\35 \color{red}{-7} &<7+7x \color{red}{-7} \\28 &< 7x \\ \dfrac{28}{\color{red}{7}} &< \dfrac{7x}{\color{red}{7}} \\ 4&< x \end{align}||
Remarque : |4<x,| c'est la même chose que |x>4.|
Comme il n'y a pas d'égalité dans cette inéquation, un point vide indiquera l'extrémité de l'inéquation.

Exemples d'inéquations dans l'univers des nombres entiers
|\{x \in \mathbb{Z} \mid -2 < x < 3 \}|
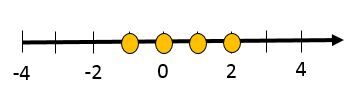
|\{x \in \mathbb{Z} \mid -2 \le x \le 3 \}|
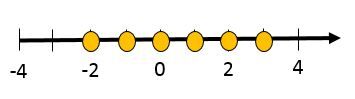
Il est aussi possible d'exprimer l'ensemble-solution d'une inéquation en intervalles ou en accolades.
Les accolades ne peuvent être utilisées que lorsque l'ensemble-solution fait partie des nombres entiers. Il suffit de faire la liste des réponses possibles.
|\{x \in \mathbb{Z} \mid -2 < x < 3 \}| |\to| |\{-1, 0, 1, 2 \}|
|\{x \in \mathbb{Z} \mid -2 \le x \le 3 \}| |\to| |\{-2, -1, 0, 1, 2, 3 \}|
|\{x \in \mathbb{Z} \mid x \le 3 \}| |\to| |\{..., -2, -1, 0, 1, 2, 3 \}|
L'intervalle doit être utilisé lorsque l'ensemble-solution fait partie des nombres réels et qu'il admet tous les nombres entre les deux bornes de l'intervalle. Il est alors important de faire attention au sens des crochets. L'infini |(\infty)| n'est jamais inclus dans l'intervalle.
|\{x \in \mathbb{R} \mid -5 \le x < 6 \}| |\to| |[-5, 6[|
|\{x \in \mathbb{R} \mid x < 4 \}| |\to| |]-\infty, 4[|
|\{x \in \mathbb{R} \mid x \ge 6 \}| |\to| |[6, +\infty[|