Les zéros d'une fonction trigonométrique

Il ne faut jamais oublier que lorsqu'on travaille avec une fonction trigonométrique, celle-ci est périodique. Il faut donc vérifier dans quel intervalle on travaille pour donner toutes les valeurs recherchées.  

1. On détermine la période de la fonction grâce à la formule |P = \displaystyle \frac{2 \pi}{ \mid b \mid}|.

2. On résout l'équation |f(x)=0|.

• On isole l'expression |\sin(b(x-h)).|

• On cherche le ou les angles qui ont la valeur du sinus. Il faut regarder dans le cercle trigonométrique si la valeur est remarquable sinon, on peut utiliser la calculatrice avec la fonction arc sinus.

• Chacun des angles précédents est égal à l'expression |b(x-h)|, on isole alors |x.|

3. On donne l'ensemble-solution en tenant compte de la période de la fonction.

Soit la fonction |f(x)=\displaystyle  -2\sin(\frac{1}{2}(x-1))+1|.

1. La période de la fonction est: |\displaystyle P = \frac{2\pi}{\mid b \mid} = \frac{2\pi}{\mid \frac{1}{2} \mid} = 4 \pi|.

2. On résout |f(x)=0|.
|\begin{eqnarray*} 0 &=& -2\sin(\frac{1}{2}(x-1))+1 \\
 -1 &=&  -2\sin(\frac{1}{2}(x-1)) \\
 \frac{1}{2} &=& \sin(\frac{1}{2}(x-1)) \end{eqnarray*}|

À cette étape, on cherche dans le cercle trigonométrique où sont situées les valeurs du sinus de |\frac{1}{2}|. On cherche dans le cercle trigonométrique puisque |\frac{1}{2}| est une valeur remarquable du sinus.

Il y a deux endroits où le sinus vaut |\frac{1}{2}|: à |\frac{\pi}{6}| radian et |\frac{5 \pi}{6}| radians.

Ces deux valeurs sont donc égales à |\frac{1}{2}(x-1)|.

Il ne reste qu'à isoler |x|.

|\begin{eqnarray*}
\frac{\pi}{6}&=& \frac{1}{2}(x-1) \\
2 \times \frac{\pi}{6} &=&  x-1 \\
\frac{\pi}{3} &=& x -1 \\
\frac{\pi}{3} + 1 &=& x  \end{eqnarray*}|
et
|\begin{eqnarray*}
\frac{5\pi}{6} &=& \frac{1}{2}(x-1) \\
2 \times \frac{5\pi}{6} &=& x -1 \\
\frac{5\pi}{3} &=& x - 1 \\
\frac{5\pi}{3} + 1 &=& x \end{eqnarray*}|

3. Les deux zéros sont donc | \frac{\pi}{3}+1| radians et |\frac{5\pi}{6}+1| radians.
Il ne reste plus qu'à donner l'ensemble-solution en tenant compte de la période de la fonction.
zéros de |f|: |\lbrace \frac{\pi}{3} + 1 + 4\pi n\rbrace \cup \lbrace \frac{5\pi}{6} + 1 + 4\pi n \rbrace| où |n \in \mathbb{Z}|.

Soit la fonction |f(x)=4\sin(-2x)+3|.

1. La période de la fonction est: |\displaystyle P = \frac{2\pi}{\mid b \mid} = \frac{2\pi}{\mid -2 \mid} = \pi|.

2. On résout |f(x)=0|.
|\begin{eqnarray*}
0 &=& 4\sin(-2x) + 3 \\
-3 &=& 4 \sin(-2x) \\
-\frac{3}{4} &=& \sin(-2x) \end{eqnarray*}|

À cette étape, on doit utiliser la calculatrice puisque la valeur de |-\frac{3}{4}| n'est pas une valeur remarquable.
On obtient |\arcsin(-\frac{3}{4}) \approx -0.848| radian.
On transforme cette valeur négative en une valeur positive en lui additionnant |2\pi|.
|2\pi + -0.848 = 5.435| radians.

Pour obtenir la deuxième valeur, on utilise un cercle trigonométrique.

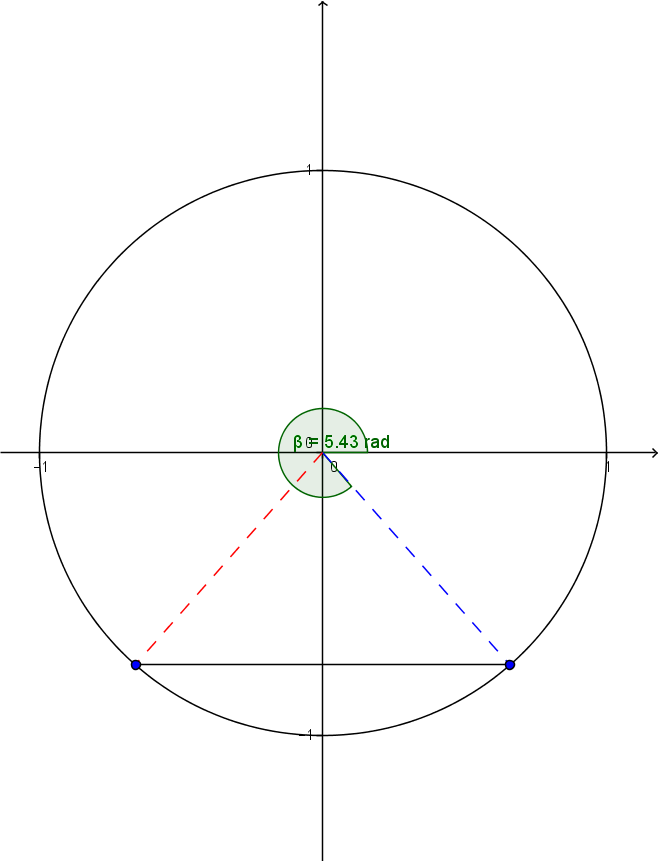
L'angle obtenu est celui indiqué en vert. On cherche maintenant l'angle formé par l'axe des |x| positifs et le segment pointillé en rouge.
On doit faire:
|2\pi - 5.435 + \pi \approx  3.99| radians

Ces deux valeurs sont donc égales à |-2x|.

|5.435 = -2x \Rightarrow x = -2.7175|
et
|3.99 = -2x \Rightarrow x = -1.995|

3. Les deux zéros sont donc |-2.7175| radians et |-1.995| radians.
Il ne reste plus qu'à donner l'ensemble-solution en tenant compte de la période de la fonction.
zéros de |f|: |\lbrace -2.7175 + \pi n \rbrace \cup \lbrace -1.995 + \pi n \rbrace| où |n \in \mathbb{Z}|.

Dans la recherche des zéros d'une fonction sinus, à l'étape où on isole |\sin(b(x-h))|, il faut absolument que |-1 \leq \sin(b(x-h)) \leq 1|. Si ce n'est pas le cas, la fonction n'admet pas de zéro. En effet, les valeurs du sinus sont comprises entre -1 et 1 tous deux inclus.

1. On détermine la période de la fonction grâce à la formule |P = \displaystyle \frac{2 \pi}{ \mid b \mid}.|

2. On résout l'équation |f(x)=0.|

• On isole l'expression |\cos(b(x-h)).|

• On cherche le ou les angles qui ont la valeur du cosinus. Il faut regarder dans le cercle trigonométrique si la valeur est remarquable sinon, on peut utiliser la calculatrice avec la fonction arc cosinus.

• Chacun des angles précédents est égal à l'expression |b(x-h),| on isole alors |x.|

3. On donne l'ensemble-solution en tenant compte de la période de la fonction.

Soit la fonction |f(x)=\displaystyle -2\cos(\frac{1}{2}(x-1))+1|.

1. La période de la fonction est: |\displaystyle P = \frac{2\pi}{\mid b \mid} = \frac{2\pi}{\mid \frac{1}{2} \mid} = 4 \pi|.

2. On résout |f(x)=0|.
|\begin{eqnarray*} 0 &=& -2\cos(\frac{1}{2}(x-1))+1 \\
-1 &=& -2\cos(\frac{1}{2}(x-1)) \\
\frac{1}{2} &=& \cos(\frac{1}{2}(x-1)) \end{eqnarray*}|

À cette étape, on cherche dans le cercle trigonométrique où sont situées les valeurs du cosinus de |\frac{1}{2}|. On cherche dans le cercle trigonométrique puisque |\frac{1}{2}| est une valeur remarquable du cosinus.

Il y a deux endroits où le cosinus vaut |\frac{1}{2}|: à |\frac{\pi}{3}| radian et |\frac{5 \pi}{3}| radians.

Ces deux valeurs sont donc égales à |\frac{1}{2}(x-1)|.

Il ne reste qu'à isoler |x|.

|\begin{eqnarray*}
\frac{\pi}{3}&=& \frac{1}{2}(x-1) \\
2 \times \frac{\pi}{3} &=& x-1 \\
\frac{2\pi}{3} &=& x -1 \\
\frac{2\pi}{3} + 1 &=& x \end{eqnarray*}|
et
|\begin{eqnarray*}
\frac{5\pi}{3} &=& \frac{1}{2}(x-1) \\
2 \times \frac{5\pi}{3} &=& x -1 \\
\frac{10\pi}{3} &=& x - 1 \\
\frac{10\pi}{3} + 1 &=& x \end{eqnarray*}|

3. Les deux zéros sont donc | \frac{2\pi}{3}+1| radians et |\frac{10\pi}{3}+1| radians.
Il ne reste plus qu'à donner l'ensemble-solution en tenant compte de la période de la fonction.
zéros de |f|: |\lbrace \frac{2\pi}{3} + 1 + 4\pi n\rbrace \cup \lbrace \frac{10\pi}{3} + 1 + 4\pi n \rbrace| où |n \in \mathbb{Z}|.

Soit la fonction |f(x)=4\cos(-2x)+3|.

1. La période de la fonction est: |\displaystyle P = \frac{2\pi}{\mid b \mid} = \frac{2\pi}{\mid -2 \mid} = \pi|.

2. On résout |f(x)=0|.
|\begin{eqnarray*}
0 &=& 4\cos(-2x) + 3 \\
-3 &=& 4 \cos(-2x) \\
-\frac{3}{4} &=& \cos(-2x) \end{eqnarray*}|

À cette étape, on doit utiliser la calculatrice puisque la valeur de |-\frac{3}{4}| n'est pas une valeur remarquable.
On obtient |\arccos(-\frac{3}{4}) \approx 2.419| radians.

Pour obtenir la deuxième valeur, on utilise un cercle trigonométrique.

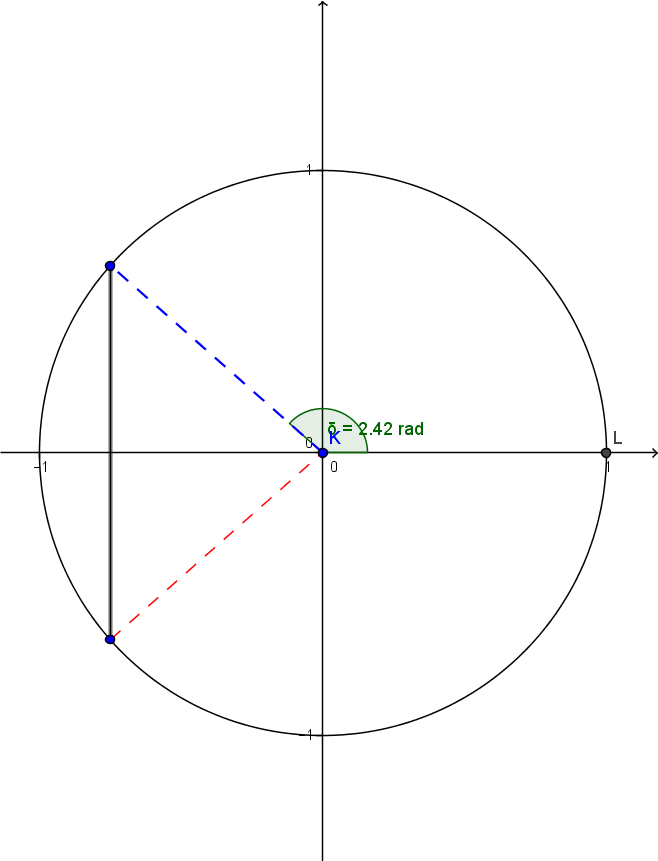
L'angle obtenu est celui indiqué en vert. On cherche maintenant l'angle formé par l'axe des |x| positifs et le segment pointillé en rouge.
On doit faire:
|2\pi - 2.419 \approx 3.864| radians

Ces deux valeurs sont donc égales à |-2x|.

|2.419 = -2x \Rightarrow x = -1.2095|
et
|3.864 = -2x \Rightarrow x = -1.932|

3. Les deux zéros sont donc |-1.2095| radians et |-.932| radians.
Il ne reste plus qu'à donner l'ensemble-solution en tenant compte de la période de la fonction.
zéros de |f|: |\lbrace -1.2095 + \pi n \rbrace \cup \lbrace -1.932 + \pi n \rbrace| où |n \in \mathbb{Z}|.

Dans la recherche des zéros d'une fonction cosinus, à l'étape où on isole |\cos(b(x-h))|, il faut absolument que |-1 \leq \cos(b(x-h)) \leq 1|. Si ce n'est pas le cas, la fonction n'admet pas de zéro. En effet, les valeurs du cosinus sont comprises entre -1 et 1 tous deux inclus.

1. On détermine la période de la fonction grâce à la formule |P = \displaystyle \frac{ \pi}{ \mid b \mid}.|

2. On résout l'équation |f(x)=0.|

• On isole l'expression |\tan(b(x-h)).|

• On cherche l'angle qui a la valeur de la tangente. Il faut regarder dans le cercle trigonométrique si la valeur est remarquable sinon, on peut utiliser la calculatrice avec la fonction arc tangente.

• L'angle précédent est égal à l'expression |b(x-h),| on isole alors |x.|

3. On donne l'ensemble-solution en tenant compte de la période de la fonction.

Soit la fonction |\displaystyle f(x)=2\tan(\frac{1}{3}(x-4))+3|.

1. La période de la fonction est: |\displaystyle P = \frac{\pi}{\mid b \mid} = \frac{2\pi}{\mid \frac{1}{3} \mid} = 3 \pi|.

2. On résout |f(x)=0|.
|\begin{eqnarray*} 0 &=& 2\tan(\frac{1}{3}(x-4))+3 \\
-3 &=& 2\tan(\frac{1}{3}(x-4)) \\
-\frac{3}{2} &=& \tan(\frac{1}{3}(x-4)) \end{eqnarray*}|

À cette étape, on cherche dans le cercle trigonométrique où est située la valeur de |-\frac{3}{2}| de la tangente. Malheureusement, cette valeur n'est pas remarquable. On doit donc utiliser la fonction |\arctan|.

|\arctan(-\frac{3}{2}) \approx -0.983| radians

Cette valeur est équivalente à |\frac{1}{3}(x-4)|.

Il ne reste qu'à isoler |x|.

|\begin{eqnarray*}
-0.983 &=& \frac{1}{3}(x-4) \\
3 \times -0.983 &=& x-4 \\
-2.949 &=& x -4 \\
-2.949+ 4 &=& x \\
1.051 &=& x \end{eqnarray*}|

3. Le zéro de la fonction est |1.051| radians.
Il ne reste plus qu'à donner l'ensemble-solution en tenant compte de la période de la fonction.
zéros de |f|: |\lbrace 1.051 + 3\pi n\rbrace| où |n \in \mathbb{Z}|.