Tracer une fonction exponentielle

1. Dans la règle de la fonction exponentielle, remplacer |x| par un minimum de 4 valeurs que l'on choisit selon la situation.

2. Trouver l'équation de l'asymptote.

3. Placer les points obtenus |(x,y)| et l'asymptote dans un plan cartésien puis relier les points pour tracer la courbe.

Trace la fonction exponentielle suivante. ||y=2(3)^x||

1. Dans la règle de la fonction exponentielle, remplacer |x| par un minimum de 4 valeurs que l'on choisit selon la situation.
   On peut remplacer |x| par les valeurs |0,| |1,| |2| et |3.| ||\begin{align} \text{Pour} \ \ x_1 &= 0, \\ y_1&=2(3)^{0}\\ &= 2 \\\\ \text{Pour} \ \ x_2 &= 1, \\ y_2 &= 2(3)^{1}\\ &= 6\\\\ \text{Pour} \ \ x_3 &= 2, \\ y_3 &= 2(3)^{2} \\ &= 18 \\\\ \text{Pour} \ \ x_4 &= 3, \\ y_4 &= 2(3)^{3}\\ &= 54\end{align}||Ainsi, on obtient la table de valeurs suivante.

|​x|	|​0|	|​1|	​|2|	​|3|
|​y|	​|\ 2\ |	​|\ 6\ |	​|18|	|54|​

2. Trouver l'équation de l'asymptote.
   
   Dans le cas présent, l'asymptote est confondue avec l'axe des ordonnées, car |k=0.|

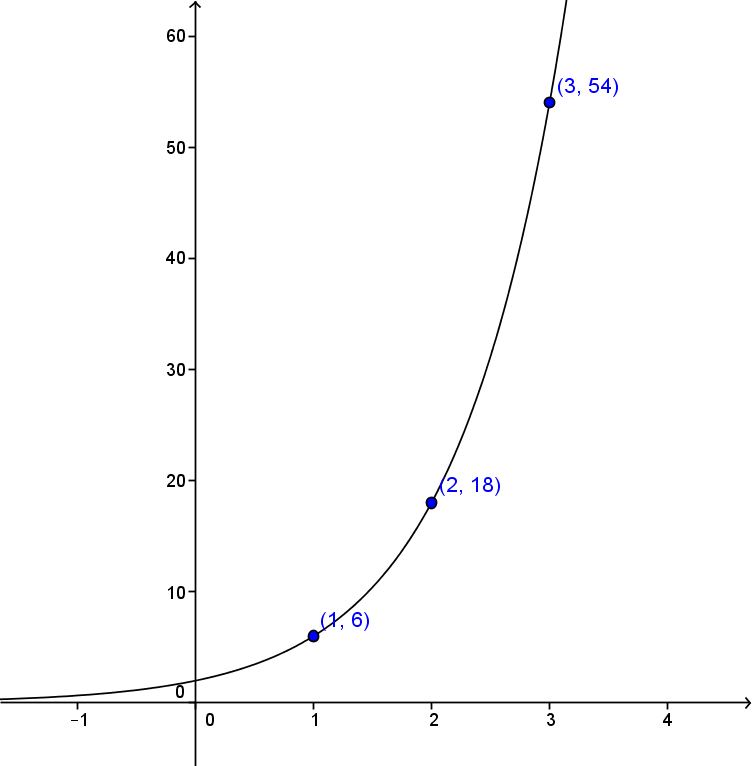
Si l'équation de la fonction exponentielle est sous la forme |y=a(c)^{x}|, on peut immédiatement déduire le point |(0,a)|. En effet, sous cette forme, le |a| correspond à la valeur initiale.

Trace la fonction exponentielle suivante.||y=4(0{,}5)^x+2||

1. Dans la règle de la fonction exponentielle, remplacer |x| par un minimum de 4 valeurs que l'on choisit selon la situation.
   Par soucis de précisions, on peut déterminer plus que 4 coordonnées des points par lesquelles passent la courbe de la fonction.||\begin{align}\text{Pour} \ \ x_1 &= -2, \\ y_1&=4(0{,}5)^{-2}+2\\&= 18 \\\\ \text{Pour} \ \ x_2 &= -1, \\ y_2 &= 4(0{,}5)^{-1}+2\\&= 10\\\\ \text{Pour} \ \ x_3 &= 0, \\ y_3 &= 4(0{,}5)^{0}+2 \\ &= 6 \\\\ \text{Pour} \ \ x_4 &= 1, \\ y_4 &= (0{,}5)^{1}+2 \\ &= 4\\\\ \text{Pour} \ \ x_5 &= 2, \\ y_5 &= 4(0{,}5)^{2}+2 \\ &= 3\\\\ \text{Pour} \ \ x_6 &= 3, \\ y_6 &= (0{,}5)^{3}+2 \\ &= 2{,}5\\\\ \text{Pour} \ \ x_7 &= 4, \\ y_7 &= 4(0{,}5)^{4}+2 \\ &= 2{,}25 \end{align}||Ensuite, il suffit de se faire une table de valeurs.

|x​|	|​-2|	|​-1|	|\ 0\ ​|	|\ 1\ |​	|\ 2\ |​	|3|​	|4|​
|y|​	|18|​	|10|​	|6|​	|4|​	|3|​	|2{,}5|​	|2{,}25|​

2. Trouver l'équation de l'asymptote.
   
   Dans le cas présent, la position de l'asymptote est définie par : ||\begin{align}y&= k \\ y&= 2\end{align}||

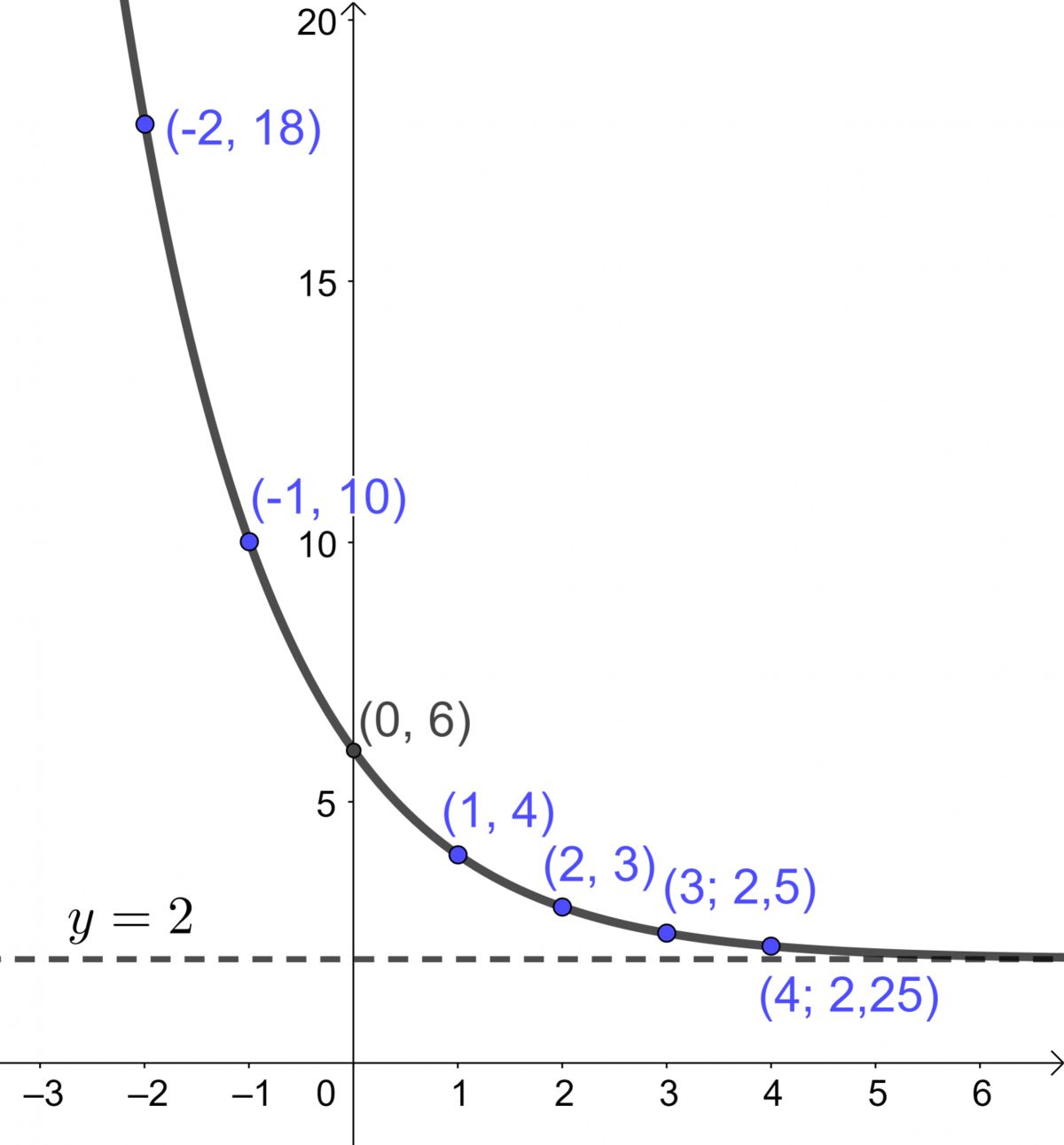
Si l'équation de la fonction exponentielle est sous la forme |y=a(c)^{x}+k|, on peut déduire l'équation de l'asymptote |y=k|. De plus, on peut placer le point |(0,\ a+k)|. En effet, sous cette forme, si on remplace |x| par |0|, il reste |a+k|, ce qui correspond à la valeur initiale.

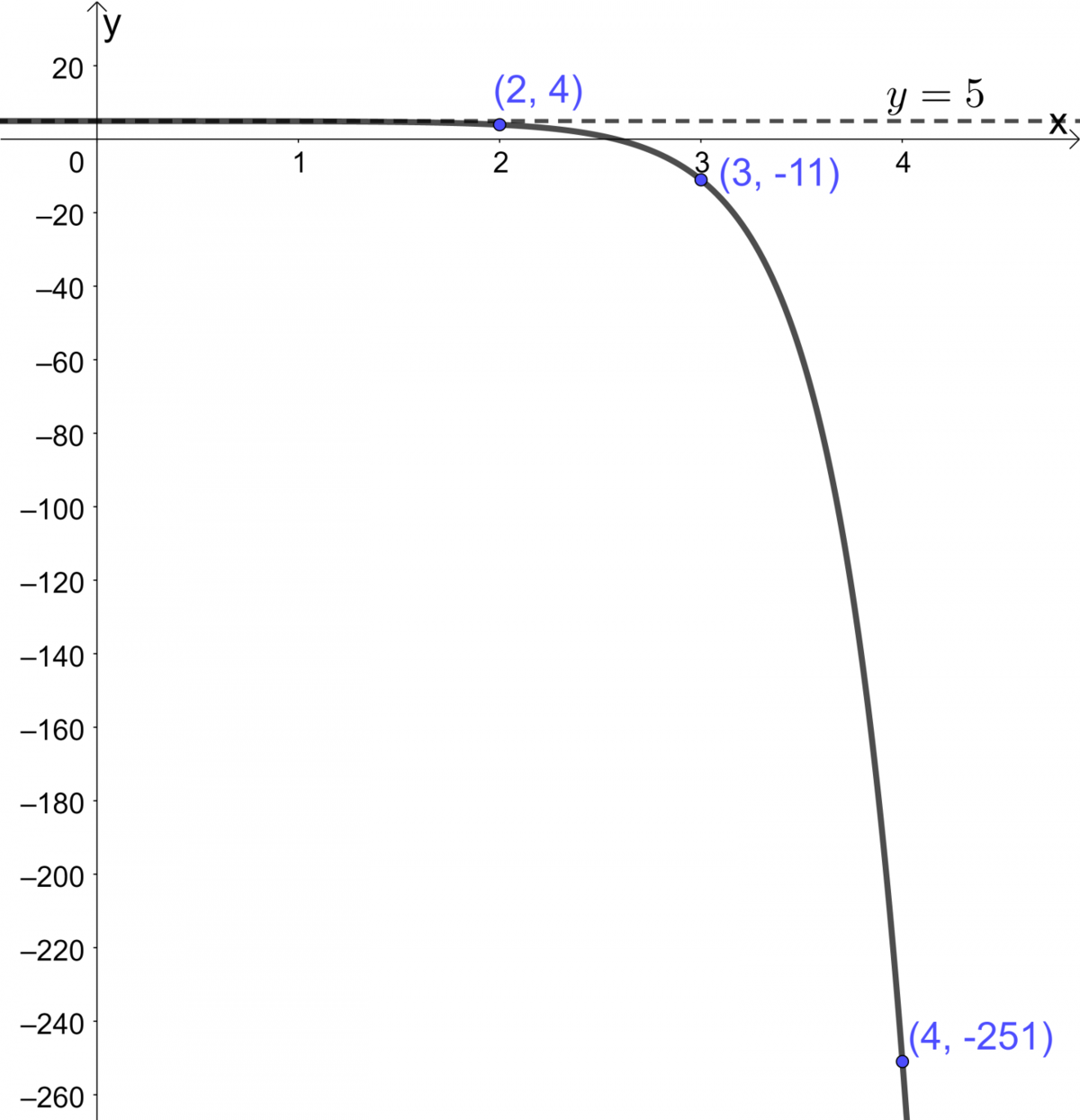
Trace la fonction exponentielle suivante.||y = -1(2)^{4(x-2)}+5||

1. Dans la règle de la fonction exponentielle, remplacer |x| par un minimum de 4 valeurs que l'on choisit selon la situation.
   On peut remplacer |x| par les valeurs |2,| |3,| |4| et |5:| ||\begin{align}\text{Pour} \ \ x_1 &= 2, \\ y_1&=-1(2)^{4(2-2)}+5\\ &= 4 \\\\ \text{Pour} \ \ x_2 &= 3, \\ y_2 &= -1(2)^{4(3 - 2)} + 5\\ &= -11\\\\ \text{Pour} \ \ x_3 &= 4,\\ y_3 &= -1(2)^{4(4 - 2)} + 5\\ &= -251 \\\\ \text{Pour} \ \ x_4 &= 5,\\ y_4 &= -1(2)^{4(5 - 2)} + 5\\ &= -4\ 091\end{align}||On a donc la table de valeurs suivante.

​|x|	|\ 2\ |​	​|3|	|4|​	|5|​
|y|​	|4|​	|-11|​	|-251|​	|-4\ 091|​

2. Trouver l'équation de l'asymptote.
   
   Dans le cas présent, la position de l'asymptote est définie par : ||\begin{align}y&= k \\ y&= 5\end{align}||

1. Tracer la fonction exponentielle de base |y=(c)^x.|

2. Effectuer le changement d'échelle verticale imposé par le paramètre |a| et la réflexion, si nécessaire.

3. Effectuer le changement d'échelle horizontale imposé par le paramètre |b| (de facteur |\dfrac{1}{{\mid}b{\mid}}|) et la réflexion, si nécessaire.

4. Effectuer la translation verticale imposée par le paramètre |k.|

5. Effectuer la translation horizontale imposée par le paramètre |h.|

Il est à noter que les quatre dernières opérations peuvent être effectuées dans n'importe quel ordre.

Trace la fonction exponentielle suivante.||y=2(2)^{-3(x+4)}-3||

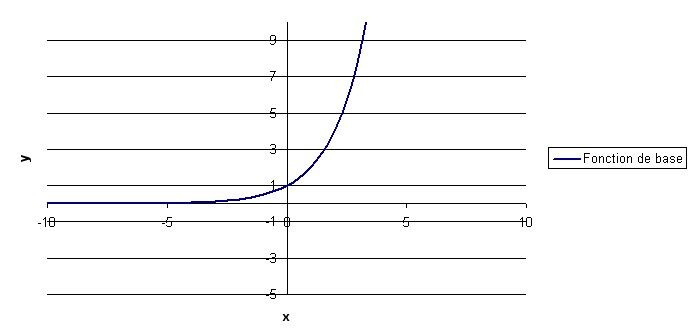
1. Tracer la fonction exponentielle de base |y=(c)^x.|
   Dans cet exemple, ||\begin{align}y&=(c)^x \\ y&= (2)^x \end{align}||

2. Effectuer le changement d'échelle verticale imposé par le paramètre |a| et la réflexion, si nécessaire.
   
   Comme le paramètre |a| est égal à |2,| il faut « étirer » verticalement la courbe d'un facteur |2.| Concrètement, cela signifie qu'il faut multiplier par |2| les valeurs de |y| de la fonction de base.

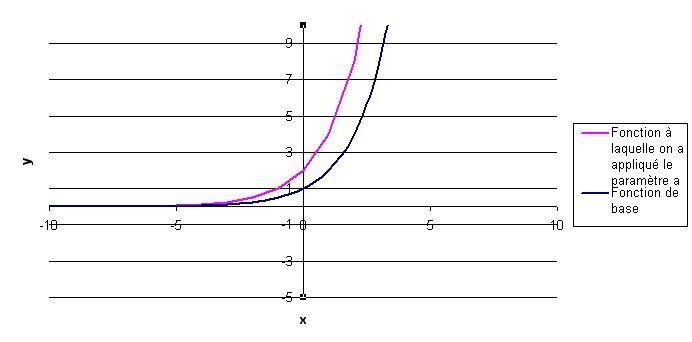
3. Effectuer le changement d'échelle horizontale imposé par le paramètre |b| (de facteur |\dfrac{1}{\mid b \mid}|) et la réflexion, si nécessaire.
   
   Comme le paramètre |b| est égal à |-3,| il faut effectuer une réflexion de la courbe par rapport à l'axe des |y| et « contracter » horizontalement la courbe d'un facteur |\dfrac{1}{3}|. Concrètement, cela revient à diviser par |-3| les valeurs de |x| de la fonction de base.

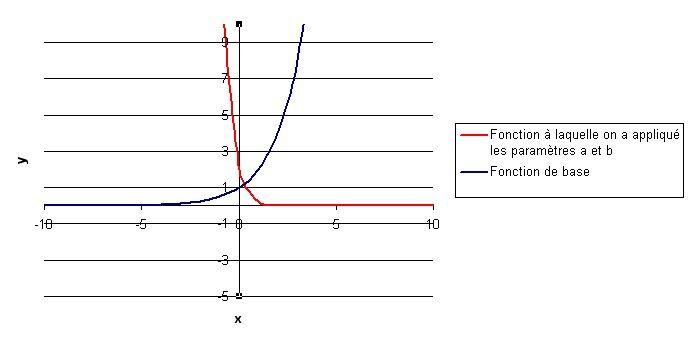
4. Effectuer la translation verticale imposée par le paramètre |k.|
   
   Comme le paramètre |k| est égal à |-3,| on doit effectuer une translation verticale de |3| unités vers le bas.

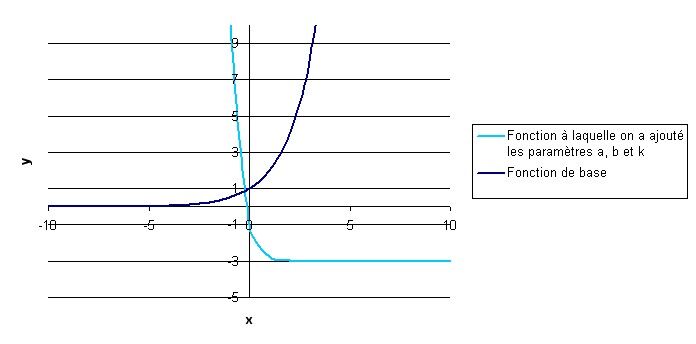
5. Effectuer la translation horizontale imposée par le paramètre |h.|
   
   Comme le paramètre |h| est égal à |-4,| |\big(x-(-4)\big),| on doit effectuer une translation horizontale de |4| unités vers la gauche.

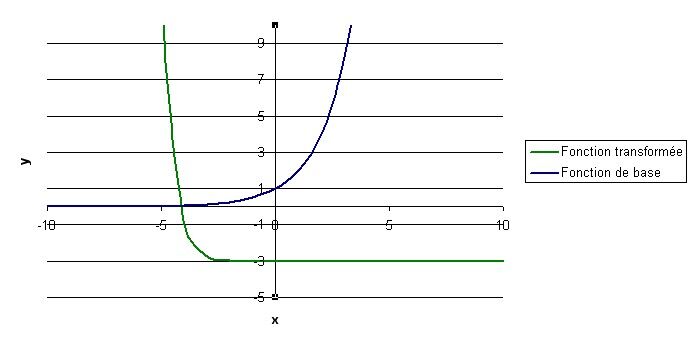
On obtient ainsi la courbe recherchée.

On peut vérifier quelques caractéristiques de la courbe obtenue :

• On obtient une asymptote à |y = -3,| ce qui correspond à |y = k.|

• On obtient une courbe décroissante dont les valeurs de |y| sont supérieures à |k,| ce qui correspond à un |a| positif et un |b| négatif.

Pour s'assurer que le graphique tracé correspond bien à celui demandé, voici quelques points importants à vérifier :

• La position de l'asymptote (avec le paramètre |k|).

• Les réflexions par rapport aux 2 axes (avec les paramètres |a| et |b|).

• La croissance ou la décroissance de la fonction.