Matières
Niveaux
Les notions abordées dans cette fiche dépassent celles qui sont vues au secondaire. Il s'agit ici d'un complément pour ceux et celles qui sont curieux et curieuses d'en savoir plus.
Les formules utilisées dans le mouvement rectiligne uniformément accéléré (MRUA) proviennent de l'étude graphique du mouvement. Pour déterminer ces relations, le graphique de la vitesse en fonction du temps sera utilisé.
| |v_{moy}=\displaystyle \frac{\triangle x}{\triangle t}| | |a=\displaystyle \frac{\triangle v}{\triangle t}| |
| |v_{f}=v_{i} + a \cdot {\triangle t}| | |\triangle x= v_{i} \cdot \triangle t +\displaystyle \frac{1}{2} \cdot a \cdot {\triangle t}^{2}| |
| |\triangle x= \displaystyle \frac{(v_{i} + v_{f}) \cdot {\triangle t}}{2}| | |\triangle x= v_{f} \cdot \triangle t -\displaystyle \frac{1}{2} \cdot a \cdot {\triangle t}^{2}| |
| |{v_{f}}^2={v_{i}}^2+2 \cdot a \cdot \triangle x| |
Les formules présentées ci-dessous sont déduites d'un graphique de la vitesse en fonction du temps. Le graphique ci-dessous présente les différentes variables utilisées dans les formules ci-dessous.
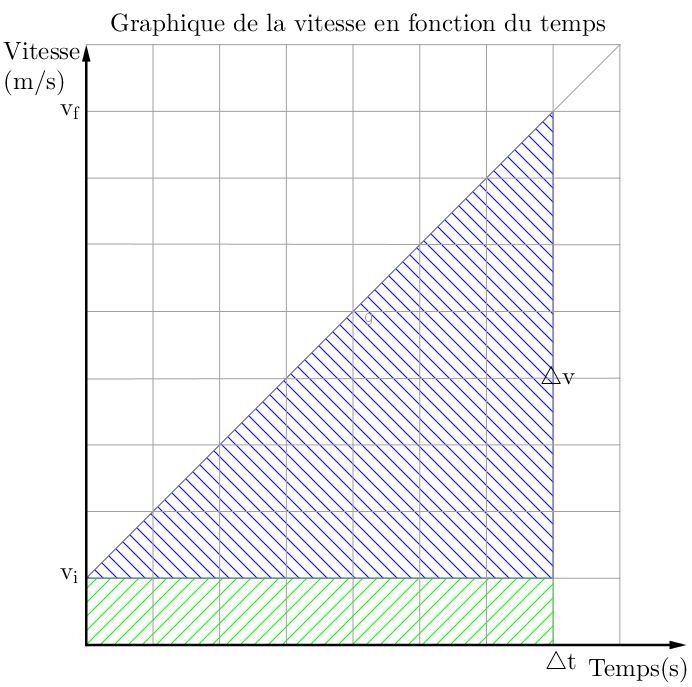
La définition de l'accélération, soit le changement de vitesse qui se produit dans un intervalle de temps, est la formule de base à utiliser. ||a = \displaystyle \frac {\triangle v}{\triangle t}|| Par produit croisé, il est possible de simplifier l'équation. ||{\triangle v}=a \cdot {\triangle t}|| On sait qu'un changement de vitesse est calculé en déterminant la différence entre la vitesse finale et la vitesse initiale. ||{\triangle v} = v_f - v_i|| En substituant cette formule dans celle trouvée à l'étape précédente, on obtient une nouvelle formule. ||v_f - v_i=a \cdot {\triangle t}|| En isolant la vitesse finale, on obtient la formule qu'il fallait démontrer. ||v_f = v_i + a \cdot {\triangle t}||
Dans le graphique ci-dessus de la vitesse en fonction du temps, on peut calculer le déplacement effectué en calculant l'aire sous la courbe. On voit dans ce graphique que l'aire sous la courbe est représentée par un rectangle vert et un triangle bleu.||\triangle x=\text {aire}_{\text { rectangle vert}} + \text {aire}_{\text { triangle bleu}}|| Pour trouver l'aire du rectangle vert, il faut multiplier la base par la hauteur. Or, la base est représentée par l'intervalle de temps, alors que la hauteur représente la vitesse initiale.||\text {aire}_{\text { rectangle vert}} = v_i \cdot \triangle t|| Pour trouver l'aire du triangle bleu, il faut multiplier la base par la hauteur et diviser le résultat par deux. Pour le triangle, la base représente l'intervalle de temps et la hauteur représente le changement de vitesse.
||\text {aire}_{\text { triangle bleu}} = \displaystyle \frac {\triangle v \cdot \triangle t}{2}|| En remplaçant les deux formules d'aires dans la formule de départ, on obtient la formule suivante.
||\triangle x=v_i \cdot \triangle t + \displaystyle \frac {\triangle v \cdot \triangle t}{2}|| Afin de simplifier la formule, il faut remplacer le changement de vitesse. Pour ce faire, nous utiliserons la formule de l'accélération.
||a = \displaystyle \frac {\triangle v}{\triangle t}|| Par produit croisé, on simplifie l'expression afin d'obtenir la formule suivante.
||{\triangle v}=a \cdot {\triangle t}|| Ainsi, en substituant cette formule dans celle trouvée plus tôt, on obtient le résultat suivant.
||\triangle x=v_i \cdot \triangle t + \displaystyle \frac {a \cdot {\triangle t} \cdot \triangle t}{2}|| Finalement, en regroupant les termes semblables ensemble, on obtient la formule à démontrer.||\triangle x= v_{i} \cdot \triangle t +\displaystyle \frac{1}{2} \cdot a \cdot {\triangle t}^{2}||
Dans le graphique ci-dessus de la vitesse en fonction du temps, on peut calculer le déplacement effectué en calculant l'aire sous la courbe. On voit dans ce graphique que l'aire sous la courbe est représentée par un trapèze.||\triangle x=\text {aire}_{\text { trapèze}}|| La formule à utiliser pour calculer l'aire d'un trapèze est la suivante.
||\triangle x=\displaystyle \frac {(B + b) \cdot h}{2}|| En analysant le graphique, on note que la grande base représente la somme de la vitesse initiale et du changement de vitesse, la petite base représente la vitesse initiale et que la hauteur représente la hauteur du trapèze.
||\triangle x=\displaystyle \frac {((v_i + \triangle v) + v_i) \cdot \triangle t}{2}|| Or, un changement de vitesse est défini par la différence entre la vitesse finale et la vitesse initiale.
||\triangle v=v_f-v_i|| En substituant cette formule dans celle de l'aire du trapèze, on obtient le résultat suivant.
||\triangle x=\displaystyle \frac {((v_i + v_f-v_i) + v_i) \cdot \triangle t}{2}|| Finalement, en simplifiant, on obtient la formule à démontrer.||\triangle x=\displaystyle \frac {(v_f + v_i) \cdot \triangle t}{2}||
Dans le graphique ci-dessus de la vitesse en fonction du temps, on peut calculer le déplacement effectué en calculant l'aire sous la courbe. On voit dans ce graphique que l'aire sous la courbe est représentée par un rectangle vert et un triangle bleu.||\triangle x=\text {aire}_{\text { rectangle vert}} + \text {aire}_{\text { triangle bleu}}|| Pour trouver l'aire du rectangle vert , il faut multiplier la base par la hauteur. Or, la base est représentée par l'intervalle de temps, alors que la hauteur représente la vitesse initiale.||\text {aire}_{\text { rectangle vert}} = v_i \cdot \triangle t|| Pour trouver l'aire du triangle bleu, il faut multiplier la base par la hauteur et diviser le résultat par deux. Pour le triangle, la base représente l'intervalle de temps et la hauteur représente le changement de vitesse.
||\text {aire}_{\text { triangle bleu}} = \displaystyle \frac {\triangle v \cdot \triangle t}{2}|| En remplaçant les deux formules d'aires dans la formule de départ, on obtient la formule suivante.
||\triangle x=v_i \cdot \triangle t + \displaystyle \frac {\triangle v \cdot \triangle t}{2}|| Afin de simplifier la formule, il faut remplacer le changement de vitesse. Un changement de vitesse est défini par la différence entre la vitesse finale et la vitesse initiale.
||\triangle v=v_f-v_i|| En substituant cette formule dans celle de l'étape précédente, on obtient l'expression suivante.
||\triangle x=v_i \cdot \triangle t + \displaystyle \left( \frac {v_f-v_i} {2} \right)\cdot \triangle t|| Pour simplifier le calcul, on effectue la distributivité du temps.
||\triangle x=v_i \cdot \triangle t + \displaystyle \frac {v_f\cdot \triangle t}{2}-\frac{v_i \cdot \triangle t} {2}|| Étant donné qu'il existe deux termes semblables, on les regroupe ensemble pour simplifier l'expression.
||\triangle x=\displaystyle \frac{v_i \cdot \triangle t} {2} + \displaystyle \frac {v_f\cdot \triangle t}{2}|| En multipliant par deux chacun des termes, on élimine les fractions.
||2\cdot \triangle x= v_i \cdot \triangle t + v_f \cdot \triangle t|| Ensuite, la première formule démontrée dans cette fiche sera utilisée.
||v_i = v_f - a \cdot {\triangle t}|| Par substitution, on obtient la formule suivante.
||2\cdot \triangle x= (v_f - a \cdot \triangle t) \cdot \triangle t + v_f \cdot \triangle t||Pour simplifier le calcul, on effectue la distributivité du temps.
||2\cdot \triangle x= v_f\cdot \triangle t - a \cdot \triangle t^2 + v_f \cdot \triangle t|| Étant donné qu'il existe deux termes semblables, on les regroupe ensemble pour simplifier l'expression.
||2\cdot \triangle x= 2 \cdot v_f\cdot \triangle t - a \cdot \triangle t^2|| En divisant par deux chacun des termes, on obtient la formule à démontrer.
||\triangle x= v_{f} \cdot \triangle t -\displaystyle \frac{1}{2} \cdot a \cdot {\triangle t}^{2}||
La définition de l'accélération, soit le changement de vitesse qui se produit dans un intervalle de temps, est la formule de base à utiliser. ||a=\displaystyle \frac {\triangle v}{\triangle t} = \displaystyle \frac {v_f-v_i}{\triangle t}|| Par produit croisé, il est possible de réorganiser l'équation. ||\triangle t = \displaystyle \frac {v_f-v_i}{a}|| Il faut ensuite utiliser la troisième formule démontrée dans cette fiche. ||\triangle x= \displaystyle \frac{(v_{i} + v_{f}) \cdot {\triangle t}}{2}|| En substituant cette formule dans celle trouvée à l'étape précédente, on obtient une nouvelle formule. ||\triangle x= \displaystyle \frac{(v_{i} + v_{f})}{2} \cdot \frac {(v_f-v_i)}{a}|| En multipliant les deux fractions ensemble, on obtient l'expression suivante. ||\triangle x= \displaystyle \frac{(v_{i} + v_{f})\cdot (v_f-v_i)}{2 \cdot a}|| En distribuant les termes au numérateur, on obtient l'expression suivante. ||\triangle x= \displaystyle \frac{{(v_{f}}^2 - {v_{i}}^2)}{2\cdot a}|| Par produit croisé, on obtient le résultat suivant. ||2 \cdot a \cdot \triangle x={v_{f}}^2 - {v_{i}}^2|| En isolant la vitesse finale, on obtient l'expression à démontrer. ||{v_{f}}^2 = {v_{i}}^2 + 2 \cdot a \cdot \triangle x||