Matières
Niveaux
Les principaux types de projections utilisés en dessin technique sont les suivants :
Certains concepts peuvent aider à comprendre et à bien distinguer les différents types de projections.
Une projection est la représentation d’un objet en trois dimensions sur une surface en deux dimensions.
En dessin technique, tout comme en dessin artistique, une difficulté s’impose lorsqu’on désire représenter correctement un objet en trois dimensions sur une feuille qui n’en possède que deux. Afin de rendre compte des trois dimensions de l’objet ainsi que des détails qui le caractérisent, on utilise différents types de projections.
Voici le même appareil photo représenté selon trois projections différentes.
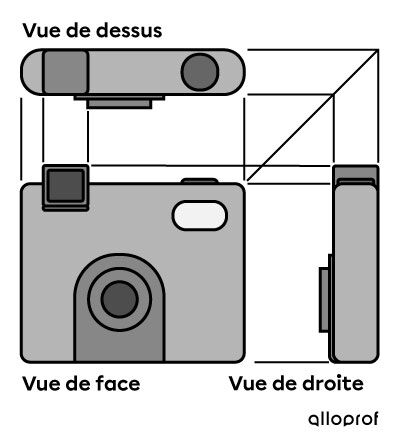
La projection à vues multiples d'un appareil photo
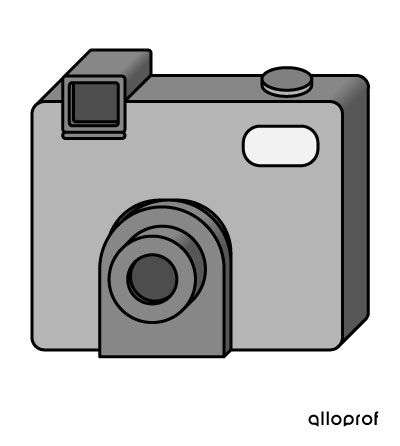
La projection oblique d'un appareil photo
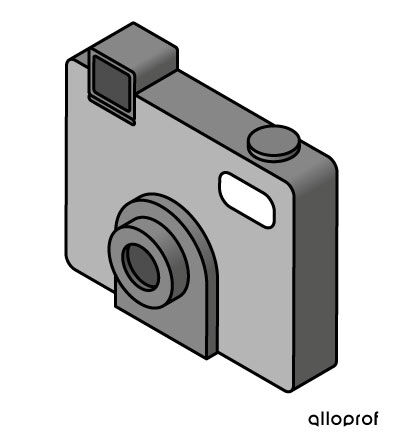
La projection isométrique d'un appareil photo
Afin de bien comprendre ce qui distingue les différents types de projections, il est essentiel d’utiliser les termes adéquats pour décrire l’espace occupé par un objet. Par convention, la terminologie suivante est utilisée en dessin technique.
| Concept | Description | Exemple |
|---|---|---|
Dimension |
Un objet occupe généralement trois dimensions dans l’espace : la longueur, la hauteur et la profondeur (ou largeur). |  |
| Mesure | Les mesures d’un objet correspondent à des valeurs numériques associées à une unité de mesure. Par convention, la cotation d’un objet est exprimée en millimètres, à moins d’indications contraires. De ce fait, les unités ne doivent pas être inscrites sur le dessin. |
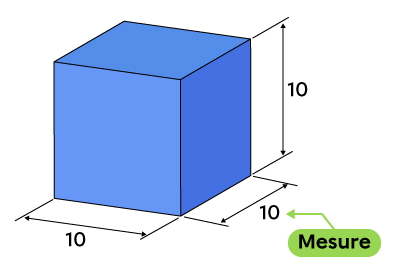 |
| Face | Une face est une surface plane. Elle possède deux dimensions (par exemple, un carré). | 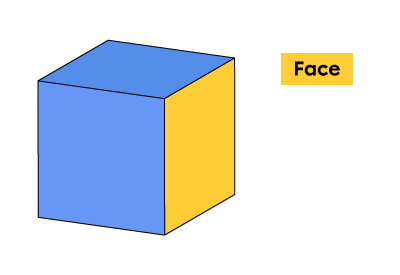 |
| Arête | Une arête est une ligne. Elle ne possède qu’une seule dimension. Elle indique les limites d’une face ou la frontière commune entre deux faces. | 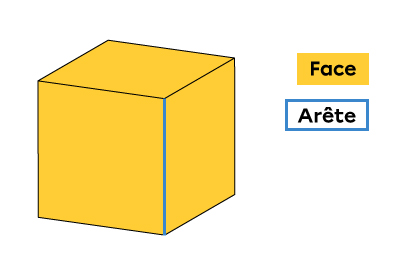 |
| Sommet | Un sommet est un point. Il ne possède aucune dimension. Il désigne le point de rencontre entre deux ou plusieurs arêtes. | 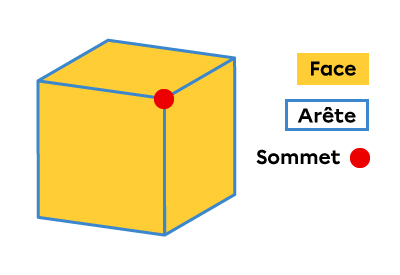 |
Une projection orthogonale est une projection dans laquelle tous les rayons visuels partant des sommets de l’objet se dirigent perpendiculairement vers un observateur placé devant la feuille.
Cette catégorie de projection comprend la projection à vues multiples et la projection isométrique.
Les types de projections se distinguent les uns des autres par deux aspects : la position de l’objet par rapport à la feuille et l’angle entre les rayons visuels et la feuille.
Dans le cas de la projection à vues multiples et de la projection isométrique, les rayons visuels partant des sommets d’un objet sont perpendiculaires à la feuille. Cela signifie qu’un observateur peut percevoir l’objet en projection à vues multiples (une vue à la fois) ou en projection isométrique en étant placé directement devant l’objet. Ces projections font ainsi partie de la catégorie des projections orthogonales.
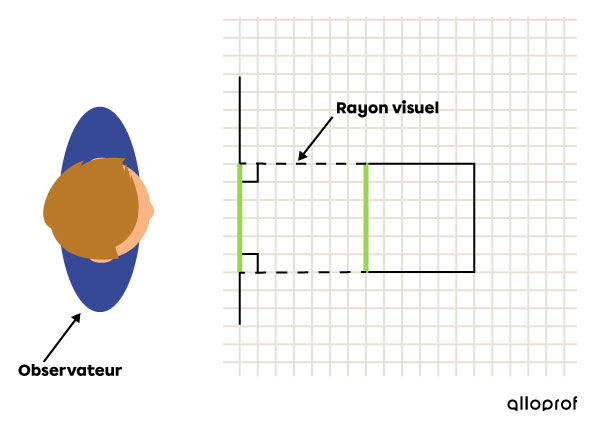
Les rayons visuels dans une projection à vues multiples
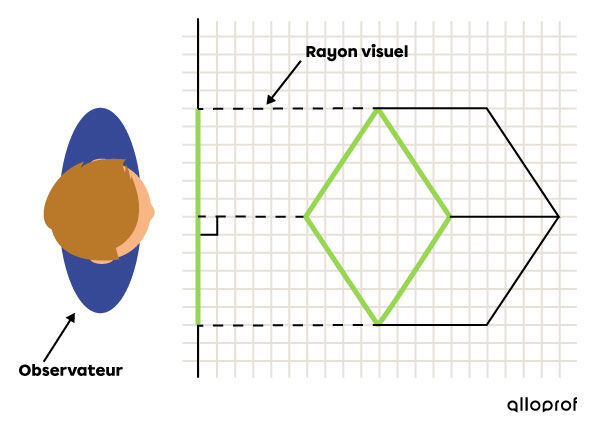
Les rayons visuels dans une projection isométrique
À l’opposé, dans la projection oblique, les rayons visuels partant des sommets sont obliques par rapport à la feuille de dessin. Autrement dit, il est impossible de percevoir un objet en projection oblique si l’observateur est placé directement devant l’objet.
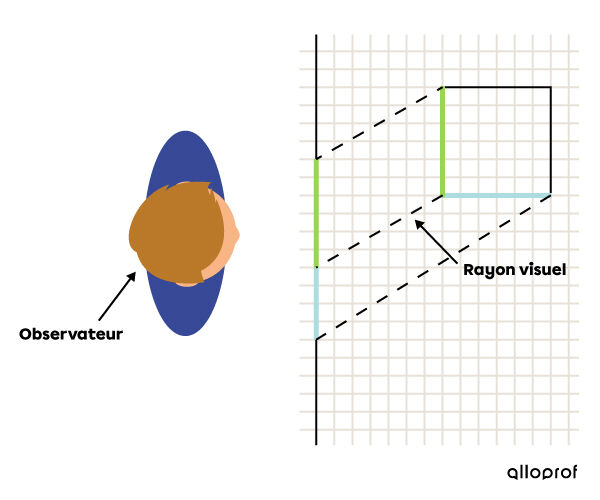
L’orientation des rayons visuels dans une projection oblique
Les projections en perspective sont des types de projections qui donnent une impression de profondeur.
Il existe différentes manières de représenter la profondeur d’un objet. On peut créer une illusion de profondeur en utilisant un point de fuite ou en utilisant des lignes d’axes parallèles. Ces deux méthodes sont présentées ci-dessous.
Tout comme les projections centrales en mathématiques, la projection en perspective avec point de fuite permet de créer l’effet de profondeur d’un objet. Dans ce cas, les droites reproduisant l’effet de profondeur convergent toutes vers un ou plusieurs points qu’on appelle points de fuite.
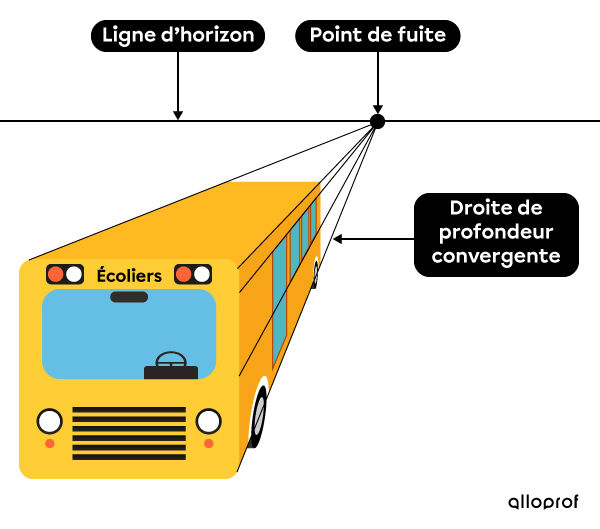
Un autobus dans une représentation en perspective avec point de fuite
L’utilisation d’un point de fuite dans une projection en perspective n’est pas recommandée en dessin technique puisque les proportions réelles de l’objet ne sont pas conservées. En effet, comme les droites de profondeur convergent toutes vers un même point de fuite, les dimensions des faces les plus éloignées sont réduites. Le point de fuite fournit donc seulement un aperçu de la profondeur. Toutefois, cette méthode permet une représentation qui ressemble à ce que l’œil d’un observateur perçoit. Par exemple, la projection en perspective avec un point de fuite crée le même effet de profondeur que la photographie.
Tout comme les projections parallèles en mathématiques, la projection en perspective à l’aide d’axes parallèles permet de créer l’effet de profondeur d’une projection sans l’utilisation de point de fuite. La projection isométrique et la projection oblique en sont des exemples. Effectivement, dans ces représentations, toutes les droites associées à la profondeur d’un objet sont parallèles entre elles. Aussi, puisqu’elles n’utilisent pas le point de fuite, ces projections sont moins conformes à ce que l’œil d’un observateur perçoit.

Un autobus dans une représentation isométrique en perspective
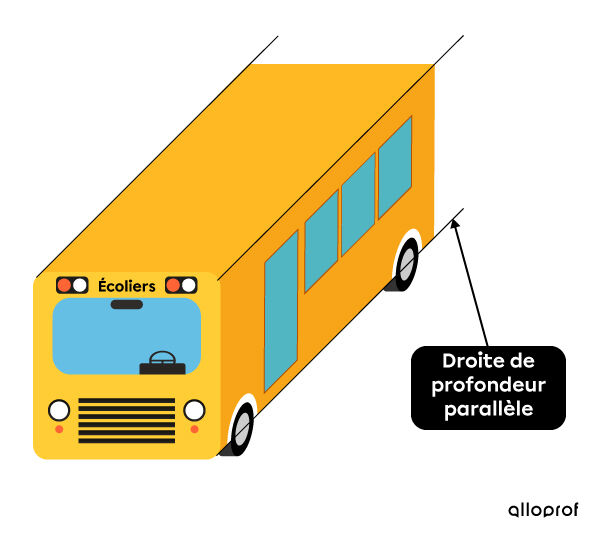
Un autobus dans une représentation oblique en perspective