Best Of
Re: Question
Bonjour!
Oui, il s'agit effectivement du Chili! :D
Si tu as d'autres questions, n'hésite pas à nous réécrire. Nous te répondrons avec plaisir!
Laurie :)
Re: Question
Bonjour!
Comme on ne voit pas la question sur la page de ton devoir, il est très difficile pour moi de t'aider. En effet, comme je ne connais ni la consigne ni ce à quoi font référence les numéros de page de le tableau, je ne suis pas en mesure de savoir ce qui est demandé.
Je t'invite à nous réécrire en ajoutant la consigne à ta question pour que nous puissions bien t'aider! :D
Laurie :)
Re: Question
Bonsoir, AluminiumArtistique6079!
Voyons les étapes de l'addition de fractions rationnelles à l'aide de l'exemple suivant.
$$ \displaystyle \frac{x}{x-2} + \frac{2}{x-1} $$
1) Factoriser le numérateur et le dénominateur de chacune des fractions.
Dans ce cas, ils sont déjà factorisés.
2) Poser toutes les restrictions (dénominateurs différents de 0).
Il faut que x-2 ne soit pas 0, donc que x ne soit pas 2.
Il faut que x-1 n'équivaille pas à 0, donc que x ne soit pas 1.
3) Simplifier les facteurs communs dans chacune des fractions (si possible).
Il n'y a pas de facteur commun à simplifier.
4) Trouver un dénominateur commun.
Multiplions (x-2) et (x-1).
$$ \displaystyle \frac{x(x-1)}{(x-2)(x-1)} + \frac{2(x-2)}{(x-1)(x-2)} $$
5) Effectuer l’addition ou la soustraction au numérateur.
$$ \begin{align} &\displaystyle \frac{x(x-1) + 2(x-2)}{(x-2)(x-1)} \\ &=\displaystyle \frac{x^2 - x + 2x - 4}{(x-2)(x-1)}\\ &=\displaystyle \frac{x^2 + x - 4}{(x-2)(x-1)}\\ \end{align} $$
6) Simplifier à nouveau les facteurs communs (si nécessaire).
Il n’y a pas de facteurs communs alors la simplification s’arrête ici.
Pour la réponse, on écrit la fraction rationnelle simplifiée en n’oubliant pas de donner les restrictions trouvées initialement.
Applique maintenant ces étapes aux deux problèmes que tu as.
N'hésite pas à poser d'autres questions!
Re: Question
Salut !
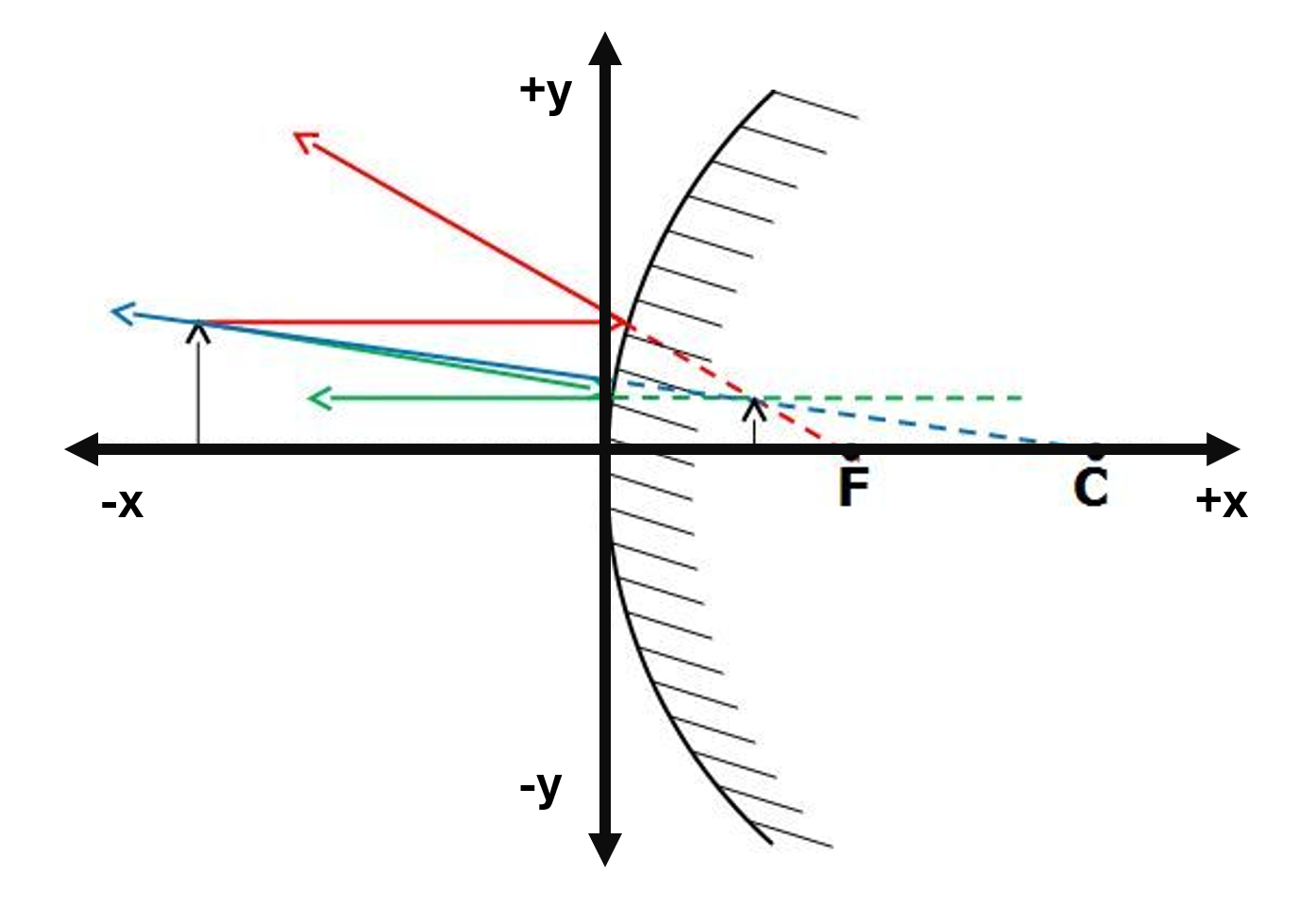
Il te faut voir le miroir comme étant le centre d'un système de référence.
Ainsi, selon la direction de l'objet ou de l'image, le signe sera positif ou négatif. Et pour 7, cette écriture permet d'avoir une valeur de grandissement positive.
J'espère que cela ait pu t'aider et si tu as d'autres questions, n'hésite pas !
Bonne journée !
Re: Question
Salut !
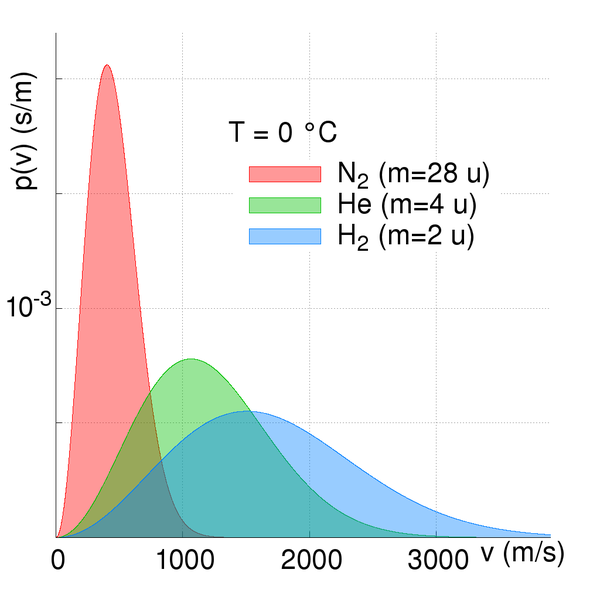
Tu peux en effet penser à un mélange entre l'effet de la gravité et la diffusion du gaz. Les particules de masses plus élevées diffusent plus lentement que les particules légères, car elles se déplacent plus lentement.
Imaginons que deux gaz diffusent vers les plus hautes altitudes, il seront ralentis par la gravité. Le plus léger aura une plus grande vitesse de diffusion et une moins grande attraction par gravité, il sera donc à plus haute altitude.
J'espère que cela ait pu t'aider et si tu as d'autres questions, n'hésite pas !
Bonne journée !
Re: Question
deux c'est un déterminant numéral et premières c'est un adjectif qualificatif.
Re: Question
Salut GoyaveResponsable5734!
Merci pour ta question. :)
Dans ce contexte, "deux" est un déterminant numéral, comme il s'agit d'un déterminant qui désigne un nombre. Pour ce qui est de "premières", c'est un adjectif qualifiant!
Je t'invite à consulter ces deux fiches pour plus d'informations sur ces concepts!
En espérant que cela répond à ta question. Si tu en as d'autres, n'hésite surtout pas à nous réécrire, il nous fera plaisir de t'aider à nouveau!
À bientôt,
Océane :)
Re: Question
Salut !
Tout d'abord, ta première réaction ne produit pas de \(CO_2\).
$$ 2H_2S+3O_2\rightarrow2H_2O+2SO_2 $$
Chaque mole de \(H_2S\) brûle pour former une mole de \(SO_2\) et chaque mole de \(CS_2\) brûle deux moles de \(SO_2\).
Tu as donc deux équations et deux inconnus, une provenant de chaque réaction.
$$ n_{SO_2}=n_{H_2S} $$
$$ \frac{m_{SO_2}}{M_{SO_2}}=\frac{m_{H_2S}}{M_{H_2S}} $$
Tu peux isoler \(m_{SO_2}\) et faire les mêmes étape pour la réaction de \(CS_2\). Finalement, cela te fera deux équations et deux variables.
- Somme des masse de 80,0g
- relation entre les masses de \(SO_2\) et de \(CO_2\) produites.
Puis tu résous le sustème d'équation pour te donner les masses et ensuite la réponse de 60,9%.
Bonne continuation !
Re: Question
Salut !
Je peux comprendre ton ressenti. À mon avis, tu peux utiliser différentes stratégies te permettant de mieux réussir. Par exemple, il te faut bien segmenter ton étude.
Prenons en exemple les mathématiques. La première étape est d'écouter en cours attentivement en prenant des notes. Tu peux ensuite relire ces notes et poser identifier ce que tu n'as pas compris. Tu peux poser des questions à ce moment à ton enseignant ou enseignante ou encore ici dans la Zone d'entraide.
Puis, tu peux penser à t'exercer avec des problèmes. Tu essayes de compléter les exercices par toi-même dans un premier temps, car c'est en faisant des erreurs qu'on apprend le mieux. Finalement, tu peux poser des questions sur tes erreurs pour les corriger tout en continuant à t'exercer.
Dans tous les cas, n'hésite jamais à utiliser les outils à ta disposition, que ce soit ici ou à ton école. Tu peux aussi visiter la fiche ci-haut pour des trucs pour ton étude.
J'espère que cela ait pu t'aider et si tu as d'autres questions, n'hésite pas !
Bonne soirée !
Re: Question
Bonjour!
Nous avons plusieurs jeux disponibles en application! :D
Voici les jeux disponibles en application :
- Magimot (pour les mots de vocabulaire)
- Fin Lapin (pour les tables)
- Grimoire (pour la lecture)
- Potager en péril (pour les classes de mots)
- Réaction solitaire (balancement d'équation chimique - pour le secondaire)
Pour les participes passé, nous avons le jeu PP l'archer! Il n'est pas disponible en application, mais tu peux y jouer avec un ordinateur! :D
Voici le lien :
Si tu as d'autres questions, n'hésite pas à nous réécrire. Nous te répondrons avec plaisir!
Laurie :)