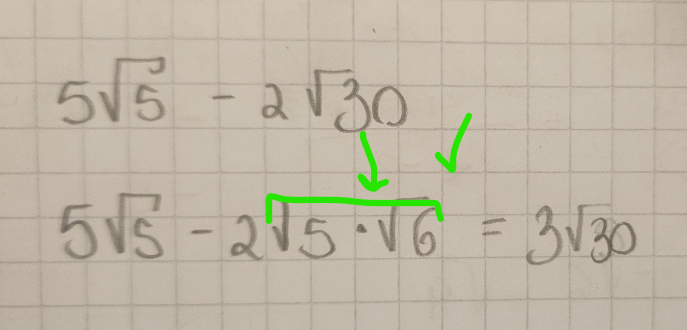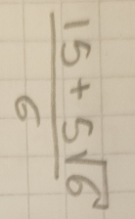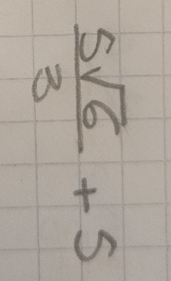Best Of

Salut!

Cette étape est correcte :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Tu peux en effet diviser la racine carrée de 30 en deux racines carrées de facteurs de 30.

Cependant, je n'arrive pas à comprendre comment tu as obtenu 3√30. Si tu calcules la valeur numérique des deux côtés de l'équation, tu constateras que le résultat n'est pas le même.

$$3\sqrt{30} ≈ 16,4317$$

$$5\sqrt{5}-2\sqrt{5}\sqrt{6} ≈ 0,2259$$

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

La seule chose que tu peux faire pour simplifier davantage cette expression, c'est factoriser √5 :

$$\sqrt{5}(5-2\sqrt{6})$$

Je t'invite à nous réécrire pour nous expliquer ta démarche, nous pourrons ainsi t'expliquer plus clairement pourquoi ce que tu as fait est faux.

En attendant, tu peux consulter notre fiche sur les différentes opérations sur les racines, je pense que cela t'aidera justement à trouver ton erreur : Les opérations sur les racines | Alloprof

À bientôt! :)

L'usages de parenthèses clarifie l'exécution des opérations:

(15 + 5√6)/6

= 15/6 + (5√6)/6

= 5/2 + 5/√6

après simplIficatIon (le 3 pour la première fraction et le √6 pour la deuxième)

Salut!

Non, les deux fractions ne sont pas égales. Pour le vérifier, je te conseille d'utiliser ta calculatrice et de calculer le nombre décimal équivalent à chaque fraction. Cela te permettra de déterminer rapidement si la simplification que tu as faite est bonne ou non.

Tu ne peux pas simplifier davantage cette fraction :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Si tu le souhaites, tu peux séparer la fraction en deux plus petites fractions, mais l'expression n'est pas davantage simplifiée, elle est juste écrite différemment :

$$ \frac{15}{6}+\frac{5\sqrt{6}}{6}$$

On ne peut rien faire de plus sur cette expression.

Je ne suis pas sûre de comprendre ce que tu as fait pour obtenir ceci :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Je vois que tu as séparé la fraction en deux, mais comment es-tu passé du 6 au 3 comme dénominateur, et pourquoi notre 15/6 est devenu un 5? Pourrais-tu nous expliquer davantage ta logique stp? Nous t'aiderons alors à y voir plus clair :)

J'espère que cela t'aide! :)

A+

Salut !

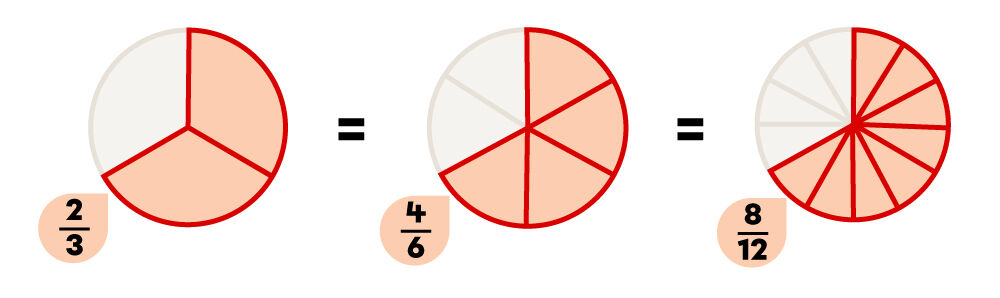
Pour compléter la réponse de DiamantTimide9860, une fraction est équivalente à une autre lorsqu’elle représente la même partie d’un tout.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

J'espère que cela ait pu t'aider et si tu as d'autres questions, n'hésite pas !

Bonne journée !

Salut !

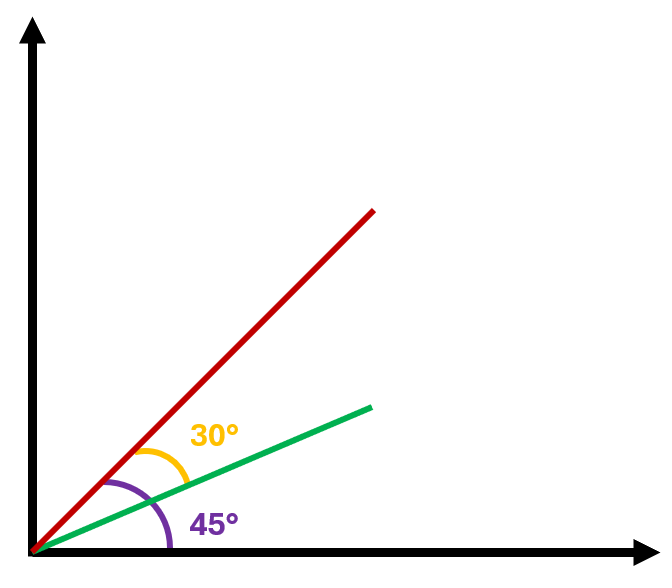
Si on devait schématiser la situation, cela donnerait cela :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

La pente de la ligne implique un angle de 45 degrés. Tu peux donc trouver l'angle de la ligne 1 ainsi que sa pente par trigonométrie.

J'espère que cela ait pu t'aider et si tu as d'autres questions, n'hésite pas !

Bonne journée !