Best Of
Re: Question
Salut!
Tes réponses sont excellentes, tout est bon et il n'y a aucune erreur, bon travail! :)
Si tu as d'autres questions, n'hésite pas à nous réécrire!
Re: Question
Salut !
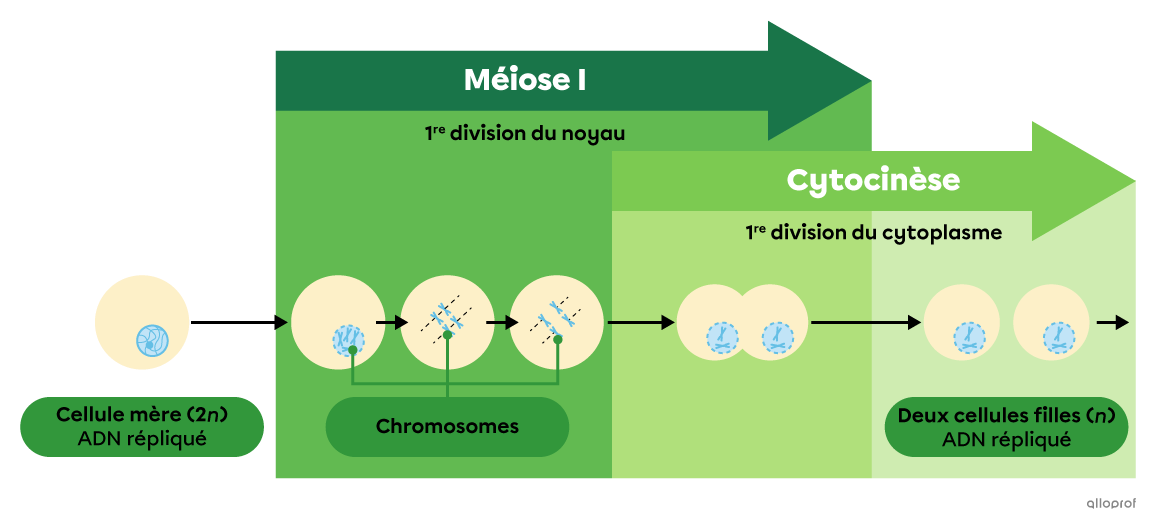
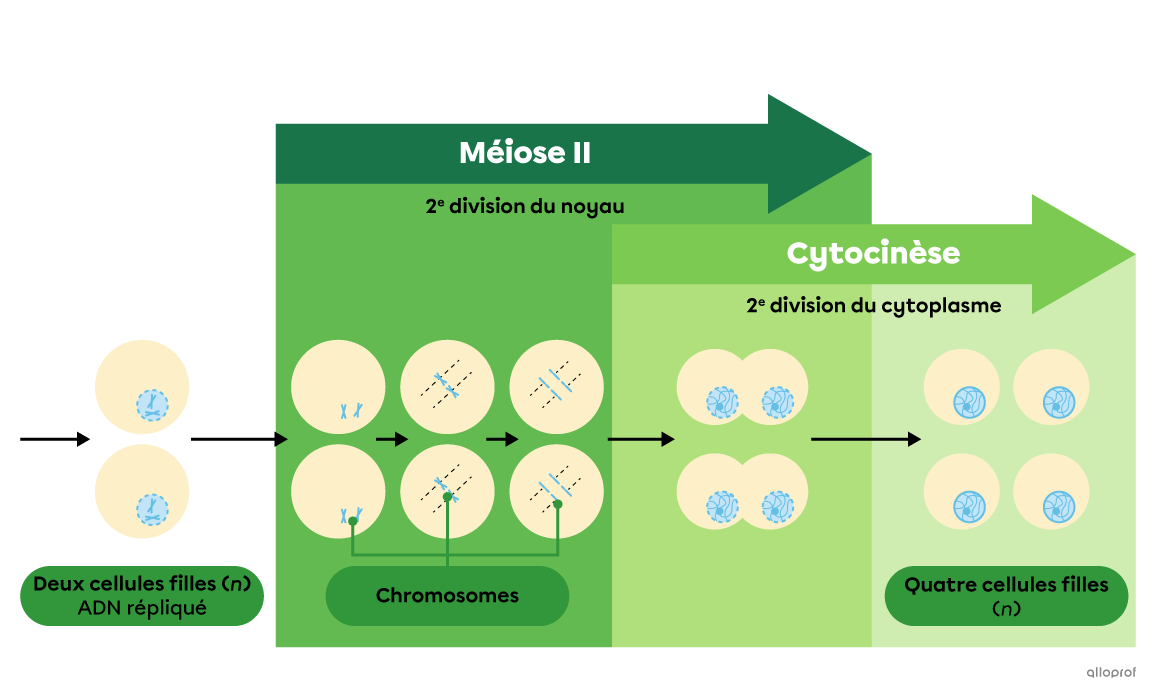
La méiose est un processus de division cellulaire qui permet la formation des cellules sexuelles (gamètes).
La méiose est une division cellulaire réductrice, c’est-à-dire que le bagage génétique des cellules filles est réduit par rapport à celui de la cellule mère. En effet, la cellule mère 2n (diploïde) produit quatre cellules filles n (haploïdes).
Le chromosome sous forme de X se divise en deux. La moitié des brins dans une cellule et l'autre moitié dans une autre cellule (division). C'est cette partie que ton schéma semble montré.
J'espère que cela ait pu t'aider et si tu as d'autres questions, n'hésite pas !
Bonne soirée !
Question
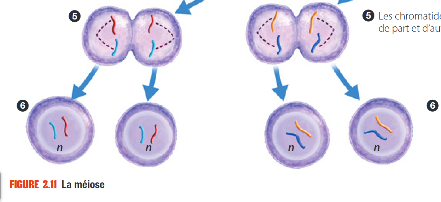
Bonjour, dans le résultat des cellules de la méiose, les 4 cellules filles sont elles différentes entre elles? Car on m'a dit qu'elles le sont mais je ne comprends pas pourquoi.
J'ai l'impression que la partie de gauche (et de droite) est pareille, non ?
Re: Question
Bonsoir! :) Merci pour ta question!
Ça tombe bien, j'avais justement répondu à la même question il n'y a pas longtemps!
Voici ma réponse: https://www.alloprof.qc.ca/zonedentraide/discussion/105120/question/p1#Comment_136036
À la suite de ta lecture, si tu as encore des questions, n'hésite surtout pas! :)
Sarah G ☺
Re: Question
Salut !
La rationalisation est la transformation en nombre rationnel du dénominateur irrationnel d'une expression écrite sous forme fractionnaire. Pour ce faire, il suffit de multiplier l'expression fractionnaire par la fraction-unité appropriée.
Par contre, il semble manquer des étapes dans l'exemple. Tu pourrais comme l'indique la fiche ci-haut, multiplier le dénominateur par \(bc\sqrt{d^2c^3}+abcd\sqrt{c^2d^4}\) comme ceci :
$$ \frac{-cd\sqrt{ba^3}-ab^2\sqrt{c^4d^5}}{bc\sqrt{d^2c^3}-abcd\sqrt{c^2d^4}}\times\frac{bc\sqrt{d^2c^3}+abcd\sqrt{c^2d^4}}{bc\sqrt{d^2c^3}+abcd\sqrt{c^2d^4}} $$
Cela devrait simplifier une partie de l'expression comme cet exemple :
J'espère que cela ait pu t'aider et si tu as d'autres questions, n'hésite pas !
Bonne soirée !
Re: Question
Voici les noms pour chacun des points cardinaux:
Nord: Boréal et Septentrional
Sud: Austral et Méridional
Ouest: Occidental
Est: Oriental
J'espère que cela va aider!
Re: Question
Hi EndorHumble1929 😊
Thanks for your question!
H2O, water, is a molecule.
A molecule is a group of at least two chemically bonded atoms.
See this worksheet for more details.
Hope it helps! 😎
See you on the Help Zone! 😁
Re: Question
Bonsoir, FraiseAdorable5247!
Les deux composées ne sont pas égales.
$$ 1+(\sqrt{x})^2\neq\sqrt{1+x^2} $$
Donc, la composition n'est pas une opération commutative. Ainsi, les domaines ne sont pas les mêmes.
Dans le cas f○g, on commence avec la racine d'un nombre quelconque, donc évidemment qu'il y a une contrainte. Le domaine doit refléter cela.
Dans le cas g○f, on commence avec une expression qui est positive. Si on ajoute une racine, cela reste positif. Il n'y a donc aucune contrainte.
Ainsi, tu vois que les domaines ne sont pas les mêmes.
Pour mieux comprendre, essaie avec une valeur.
On ne pourrait pas mettre -1 dans l'expression
$$ 1+(\sqrt{x})^2 $$
Par contre, on pourrait mettre -1 dans l'expression
$$ \sqrt{1+x^2} $$
J'espère que cela t'éclaircit!
Re: Question
Bonsoir, FraiseAdorable5247!
L'image d'une fonction correspond à l'ensemble des valeurs que peut prendre la variable dépendante.
Je doute que tu doives trouver l'image de n'importe quelle fonction puisque tu n'es qu'en secondaire 5. Je t'invite à nous partager tes exercices et nous pourrons mieux te guider.
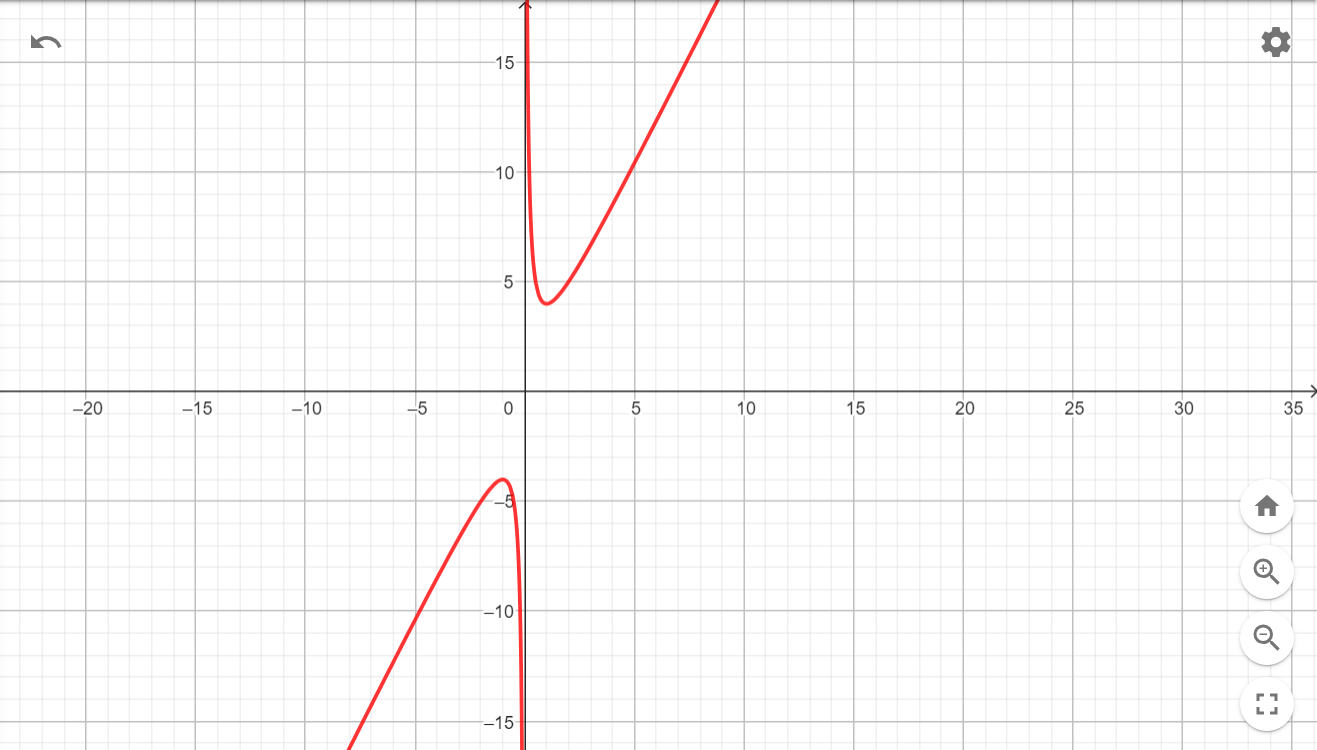
À titre d'exemple, voici le graphique de 2(1+x²)/x.
Pour donner l'image avec précision, on utilise des connaissances postsecondaires de dérivées et de valeurs critiques.
On calcule entre autres que 2(1+x²)/x=0 pour x=-1 et x=1. Lorsqu'on pose ces valeurs dans l'expression, on obtient y=-4 et y=4. On obtiendra l'image (−∞,−4]∪[4,+∞).
Tu pourras apprendre cela l'an prochain!
Re: Question
L'ordonnée à l'origine de la fonction se calcule en remplaçant x par 0 . f(0)=−2[12(0+1)]+2f(0)=2 f ( 0 ) = − 2 [ 1 2 ( 0 + 1 ) ] + 2 f ( 0 ) = 2 L'ordonnée à l'origine est donc 2.