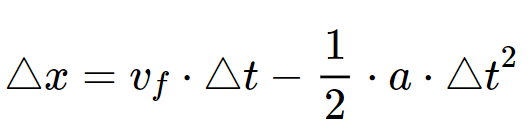Best Of
Re: Question
Salut LapinMauve8378 😁
Merci pour ta question!
C'est plutôt l'inverse, on a nommé les ions atomiques les atomes qui étaient chargés électriquement.
Voici la définition : Un ion polyatomique est un ion formé d’un groupe d’atomes liés entre eux. Un ion est un atome chargé électriquement après avoir subi une perte (+1) ou un gain d’électrons (-1).
Apprends-en plus ici.
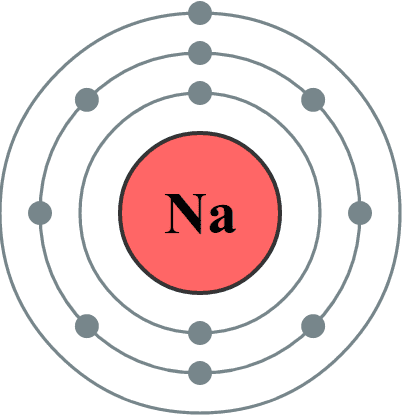
Pour répondre à ta question, prenons l'exemple du Na.
Sa configuration électronique est habituellement la suivante.
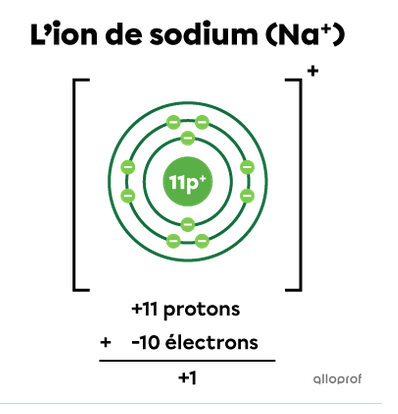
Lorsqu'il perd son électron (+1), il s'est débarrassé d'une charge négative, il devient Na+.
N'hésite pas si tu as d'autres questions 😊
À bientôt 😎
Re: Question
Salut!
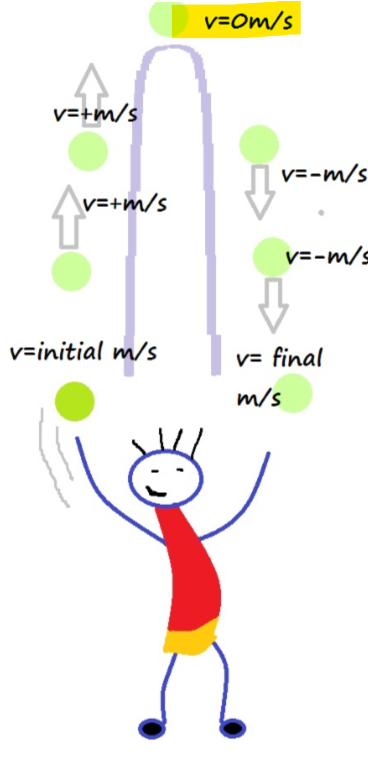
On lance l’objet verticalement, donc parfaitement vers le haut. Lorsque l’objet quitte notre main et est dans les aires, il n’y a aucune force externe appliquée sur lui, seulement la force gravitationnelle. Ainsi, l’accélération de l’objet correspond à l’accélération gravitationnelle. Puisque l’accélération est constante, on peut utiliser les formules du MRUA.
On te dit que l'objet atteint 50% de sa hauteur maximale en 2 secondes. On peut appliquer l'équation du MRUA suivante sur l’axe des y :
Comme ceci :
$$Δy=v_{f}• Δt -0,5•a•Δt^2$$
$$y_{f}-y_{i}=v_{f}• Δt -0,5•(-9,8)•Δt^2$$
La balle part du sol, donc à y=0 :
$$y_{f}-0=v_{f}•Δt -0,5•(-9,8)•Δt^2$$
$$y_{f}=v_{f}•Δt -0,5•(-9,8)•Δt^2$$
Cela prend 2 secondes pour aller de y=0 à 50% de la hauteur maximale, donc à \(0,5•y_{max}\) :
$$0,5y_{max}=v_{f}•2 -0,5(-9,8)(2^2)$$
\(v_{f}\) est ici la vitesse à t=2, donc lorsque l'objet est à la moitié de sa hauteur maximale.
$$0,5y_{max}=2v_{t=2} -0,5(-9,8)(2^2)$$
De plus, lorsque l’objet est à sa hauteur maximale, sa vitesse est nulle (la balle monte, puis redescend lorsqu’elle atteint la hauteur maximale, donc la vitesse est nulle l'instant où la passe passe de la montée à la descente).
On peut appliquer cette formule sur l'axe des y :
Comme ceci :
$$v_{f}^2=v_{i}^2+2 •a•Δy$$
$$v_{f}^2=v_{i}^2+2(-9,8)(y_{f}-y_{i})$$
Comme mentionné, la vitesse finale est nulle lorsque la balle est à \(y_{max}\) :
$$0^2=v_{i}^2+2(-9,8)(y_{max}-y_{i})$$
$$0=v_{i}^2+2(-9,8)(y_{max}-y_{i})$$
Ici, nous n'allons pas définir le moment initial comme étant le moment lorsqu'on lance la balle, puisqu'on ne connait pas la vitesse avec laquelle on lance la balle au tout début (dans ce cas-là, on connaitrait \(y_{i}\), qui est de 0 mètre, mais on ne connaîtrait pas \(v_{i}\) !). Nous allons plutôt poser le moment où la balle est à la moitié de sa hauteur maximale comme moment initial dans cette formule, comme ceci :
$$0=v_{t=2}^2+2(-9,8)(y_{max}-0,5y_{max})$$
On a maintenant deux équations et deux inconnus, soient \(v_{t=2}\), la vitesse à t=2 secondes, et \(y_{max}\) la hauteur maximale atteinte par la balle.
$$0=v_{t=2}^2+2(-9,8)(y_{max}-0,5y_{max})$$
$$0,5y_{max}=2v_{t=2} -0,5(-9,8)(2^2)$$
Tu peux résoudre ce système d'équations pour trouver la vitesse à t=2 sec et la hauteur maximale. Finalement, tu pourras utiliser une autre équation du MRUA pour \(t\) lorsque \(y=y_{max}\).
J'espère que c'est plus clair pour toi! Si tu as d'autres questions, n'hésite pas à nous réécrire :)
Re: Question
Bonjour,
Tu dois d'abord savoir que 12 est équivalent à 12/1 .
Cela revient à faire :
12 * 3/5 ou
12/1 * 3/5 donc
(12*3) / (5*1)
Je te laisse poursuivre :)
Bonne journée !
Re: Question
Bonsoir HippocampeRapide,
Merci de faire appel à nos services! :)
Est-ce que tu aimerais savoir à quel moment utiliser « as » et à quel moment utiliser « like »? Si oui, voici quelques explications :
Généralement, lorsque l'on compare deux éléments entre eux et que ce sont des noms, on utilise « like ».
- This girl looks like her brother.
On utilise as pour comparer deux éléments lorsque c'est suivi d'un verbe.
- No one studies as I do.
Ici, comme tu peux le voir, on a le verbe «I do» après le as.
En fait, like est utilisé pour introduire une comparaison créée par un nom, tandis que as est utilisé pour introduire une comparaison crée par une phrase qui contient un verbe.
Donc, on écrit like lorsqu'un nom (sans verbe) suit (est à droite) et on écrit as lorsqu'une phrase suit (sujet + verbe) (est à droite).
J'espère que c'est plus clair pour toi! :D
N'hésite pas à nous réécrire si tu as d'autres questions!
Sarah g
Re: Question
Ok, si dans le nombre 257 394 il y a le son "deux-cent" puis "mille" ça veut dire qu'il y a deux-cent-mille. Dans l'exercice ils demandent de décomposer le nombre de la plus grande unitée à la plus petite. Dans celle-si, la plus grande unitée son les centaine de mille. Ensuite viennent les dizaine de mille, les centaines, ect.
Re: Question
Voici une façon de procéder.
Pour t'assurer que tu ne te trompes pas, choisis un point à l'intérieur de la région solution (le polygone de contraintes): ce point devrait respecter toutes les inégalités que tu auras trouvées.
Note: Quand une droite n'est pas incluse dans la région solution, on la trace en pointillé et l'inégalité est stricte (< ou >)
Par contre quand une droite est dans la région solution, on la trace en ligne pleine et l'inégalité est ≤ ou ≥.
Ici s'agit-il vraiment de droites en pointillé?
Re: Question
Bonjour,
Avec la calculatrice, pour trouver la racine carrée d'un nombre, il suffit d'entrer le nombre sur la calculatrice, puis d'appuyer sur le bouton dédié à cela. Il est souvent représenté par le symbole \( \sqrt{} \)
Sans Calculatrice, tu peux estimer la racine carrée en trouvant les carrés parfaits les plus proches de ce nombre. Par exemple, pour trouver la racine carrée de 20:
- on sait que 16 et 25 sont les carrés parfaits les plus proches, ce qui signifie que la racine carrée de 20 se situe entre 4 et 5. On peut donc obtenir une approximation de la racine carrée.
J'espère que cela t'auras été utile.
Bonne journée :)
Re: Question
Bonjour,
Je te conseil, pour chaque équation, de trouvé son abscisse et son ordonnée à l'origine. Une fois cela fait il ne te suffit que faire passer une droite à travers ces deux points.
Rappel :
L'ordonnée à l'origine est l'endroit où la droite croise l'axe des ordonnée. Elle peut être trouvée en remplaçant x par 0 dans ta fonction et en résolvant pour y.
À l'inverse, l'abscisse à l'origine est l'endroit où la droite croise l'axe des abscisses. Elle peut être trouvée en remplaçant y par 0 dans ta fonction et en résolvant pour x.
N'hésites pas si tu as d'autres questions.
Bonne journée :D
Re: Question
Salut!
Cela signifie "Culture et citoyenneté québécoise"
J'espère que je t'ai aidé ;)
Re: Question
Bonjour!
Je te suggère de consulter la réponse à la question que tu as posée plus tôt. Elle contient des conseils qui t'aideront à bien réussir ton année scolaire! :D
Aussi, aider les élèves avec Alloprof est une chose merveilleuse. Nous (moi et, je le suppose, mes collègues) sommes très fiers de pouvoir aider et supporter les élèves dans leur réussite! :D
Si tu as d'autres questions, n'hésite pas à nous réécrire. Nous te répondrons avec plaisir!
Laurie :)