Best Of
Question
Je ne comprend pas la question.
Un carré et un triangle ayant la même hauteur sont collés ensemble par un côté, calcul l'aire totale de la géométrie .
Re: Question
Salut,
Merci d'utiliser la zone d'entraide.
Il serait plus simple de t'aider avec une photo du problème, puisqu'il manque des nombres à ta question pour pouvoir bien te l'expliquer.
Mais j'ai créé un exemple fictif, pour te démontrer les calculs nécessaires.
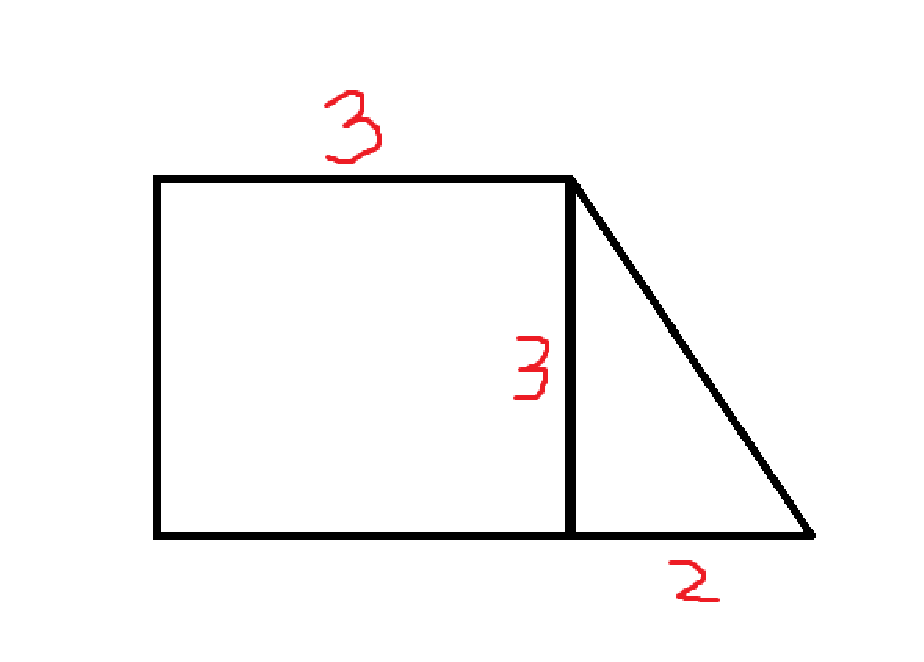
Alors premièrement, voici un carré et un triangle qui ont la même hauteur.
Nous cherchons à avoir l'air total.
Tu dois donc trouver l'air du carré, en utilisant la formule:
côté x côté
Donc, dans cet exemple, 3 x 3 = 9
Ensuite, tu dois trouver l'aire du triangle, en utilisant la formule:
base x hauteur / 2
Donc, dans cet exemple (2 x 3)/2 = 3
Donc l'air total, qui est l'addition de l'aire du carré et du triangle, est de 9 + 3 = 12
Nous n'avons pas l'unité de mesure dans cet exemple, mais il est important de le noter dans ta réponse finale.
J'espère t'avoir aidé,
Bonne soirée,
Karen
Re: Question
Salut à toi!
Merci pour ta question :)
Pi, c'est un nombre qui a un infini de décimales. On l'utilise dans la mesure de cercles (circonférence et aire). C'est probablement quelque chose que tu verras plus tard dans ton parcours!
Pour en apprendre plus sur les symboles mathématiques, c'est par ici:
J'espère que ça répond à ta question!
Bonne journée :D
Ariane
Re: Question
Salut à toi!
Merci pour ta question :)
Pour savoir rapidement si un nombre est divisible par 4, on doit additionner les deux derniers chiffres du nombre (1+0). Si ce nombre est divisible par 4, ça veut dire que ça fonctionne! Comme 1 n'est pas divisible par 4, ce nombre ne se divise pas par 4! Du moins, il se divise, mais ne donnera pas un nombre entier :)
Pour en apprendre plus sur les critères de divisibilité, c'est par ici:
J'espère que ça répond à ta question!
Bonne soirée :D
Ariane
Re: Question
Salut à toi!
Merci pour ta question :)
Normalement, dans la décomposition, on ne met pas de soustractions! Surtout quand celles-ci s'annulent (+1-1). Il y a plusieurs façons de décomposer!
Pour apprendre comment décomposer des nombres, c'est par ici:
J'espère que ça répond à ta question!
Bonne journée :D
Ariane
Re: Question
Salut à toi!
Merci pour ta patience, ta question nous a fait creuser la tête! ;)
Pour résoudre le problème, on devrait utiliser la formule suivante:
$$I=\frac{p}{s}$$
où I représente l'intensité sonore (w/m^2), P représente la puissance sonore (W) et s représente la surface. Comme la surface est ronde, on devrait utiliser 4pi(r)^2!
On pourrait donc considérer que nous sommes sur une surface de 1m^2 à la première position, et que la puissance sonore est de 4,0 x 10^-6 W. On pourra donc remplacer P par cette valeur, et multiplier par 4 la surface (donc 4m^2). On pourra ensuite trouver l'intensité de la deuxième position!
Pour calculer les décibels, on devra utiliser la formule suivante:
$$L=\log_{10}{(\frac{I}{I_{0}}})$$
L représente les décibels, I représente l'intensité et Io est une constante, soit 1,0x10^-12 w/m^2!
J'espère que ça te piste un peu!
Bonne journée :D
Ariane
Re: Question
Identifie clairement ce que tu fais, ça t'aidera énormément pour plus tard
Soit h la hauteur du cône.
La hauteur recherchée est donc h + 18
volume du cône + volume du cylindre = 565 cm³
en utilisant les formules données par Ramzi on a donc
π3²h/3 + π3²18 = 565
π3h = 565 - π162
π3h = 56.06
tu y étais presque! (d'où l'importance de mon premier commentaire)
en isolant le h, on trouve h = 5.95 arrondi à 6
donc la hauteur recherchée est h + 18 = 24
Re: Question
Bonjour à toi!
Merci pour ta question :)
Nous avons en effet une fiche qui explique les grandes lignes du texte argumentatif:
Il y a aussi, sur le site du Ministère, un recueil de texte avec les meilleurs textes de l'année 2019. Malgré que ce ne soit pas nécessairement les mêmes sujets, ça peut toujours aider!
J'espère que ça répond à ta question!
Bonne journée :D
Ariane