Best Of
Re: Question
Bonjour GrenatAuthentique3468,
Merci pour ta question!
Je te suggère d'aller consulter le répertoire de révision de secondaire 1. Il contient tous ce dont tu auras besoin.
S'il y a des notions qui te posent problème, revient nous voir, nous allons te répondre avec plaisir!
J'espère t'avoir aidé!
Lea-Kim
Re: Question
Bonsoir GrenatAuthentique3468,
Cette page pourrait te donner une idée des notions à connaître pour ton examen de fin d'année: https://www.alloprof.qc.ca/fr/eleves/bv/mathematiques/aide-memoire-mathematiques-1re-et-2e-seconda-m1519
De plus, ton cahier de révision (et si c'est le cas, ton cahier d'exercices) est un bon outil pour ta révision en vue de ton examen.
En espérant avoir répondu à ta question, bonne révision
Re: Question
Salut PapillonOptimiste7030 😁
Merci pour ta question!
La rotation de la Terre est le fait qu'elle tourne sur elle-même.
Vois-la en action ici.
La révolution de la Terre est le trajet qu'elle effectue autour du Soleil en une année, soit en 365,25 jours.
Tu connais l'émission de dance Révolution? Le nom de l'émission vient probablement du fait qu'il y a des caméras sur tout le tour de la scène pour prendre en mouvement les danseurs et les danseuses, en quelque sorte, une révolution. Ça pourrait te faire penser à ce mot pour le mouvement circulaire autour du Soleil!
N'hésite pas si tu as d'autres questions 😊
À bientôt 😎
Re: Question
Salut PapillonRose1268 😁
Merci pour ta question!
D'abord, revoyons l'équivalence suivante.
On doit donc viser une concentration en chlore inférieure à: $$4\ \text{g} / 1\ 000\ \text{L}.$$
On a 6,55 x 10^4 L.
On doit alors ne pas dépasser:
$$\frac {4\ \text{g}} {1\ 000\ \text{L}} = \frac {\text {?}\ \text{g}} {6{,}55 \times 10^4\ \text{L}};$$
$$ \text {?} = \frac {4\ \text{g} * 6{,}55 \times 10^4\ \text{L}} {1\ 000\ \text{L}} = 262\ \text{g}.$$
Les granules de chlore étant concentrées à 70%, on peut atteindre une masse de:
$$\frac {70\ \text{g}} {100\ \text{g}} = \frac {262\ \text{g}} {\text {?}\ \text{g}};$$
$$\text {?}\ \text{g} = \frac {100\ \text{g}*262\ \text{g}} {70\ \text{g}} = 374{,}29\ \text{g}.$$
Cela veut donc dire que Christine doit mettre au maximum 374,29 g de granules dans la piscine pour ne pas dépasser la quantité de chlore recommandée.
N'hésite pas si tu as d'autres questions 😊
À bientôt 😎
Re: Question
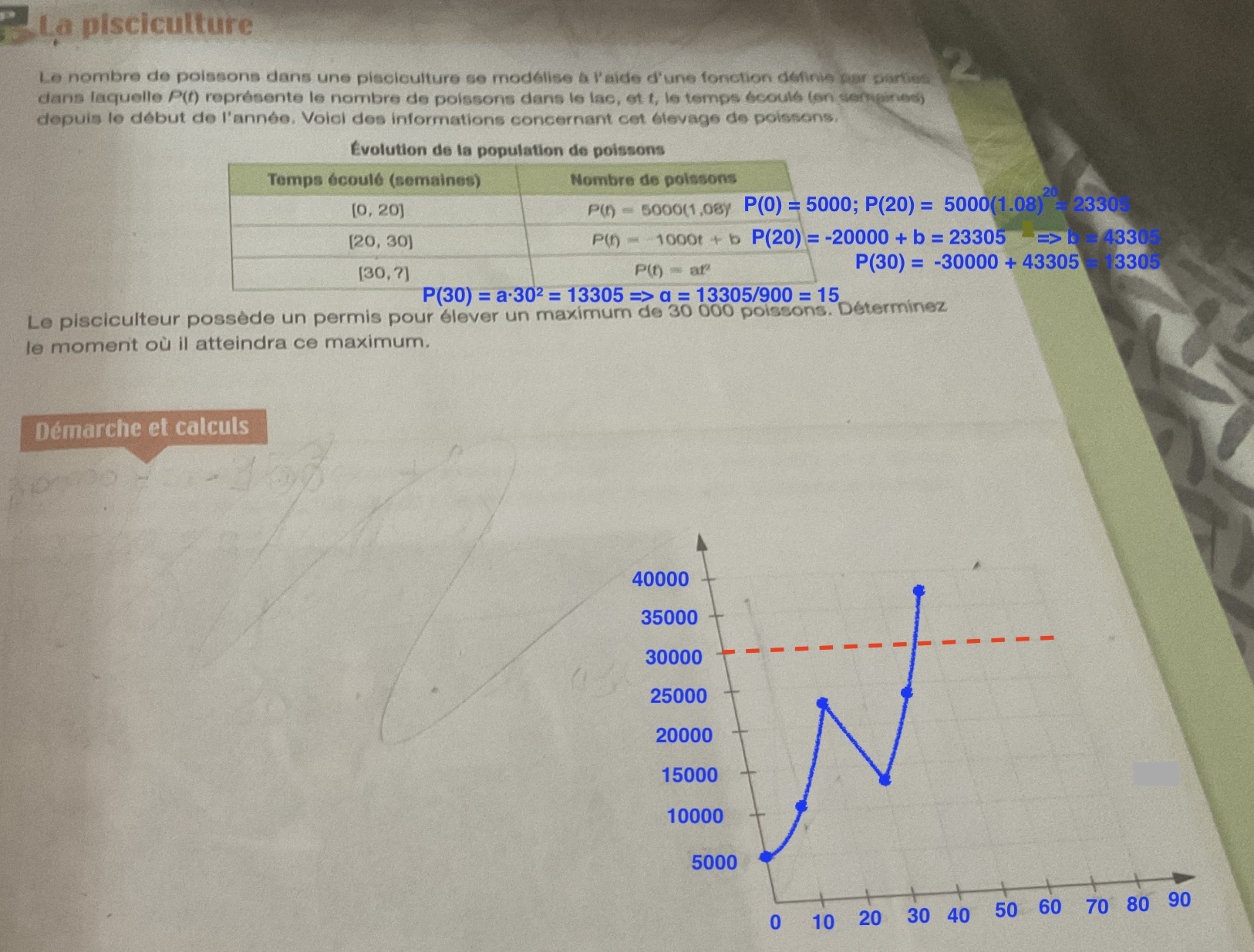
- identifie les valeurs minimales et maximales de la fonction sur le premier intervalle
- comme la fonction est continue (je présume) alors cela te donne la valeur de la fonction au début du prochain intervalle
- ce qui te permet d'identifier le paramètre manquant b
- là aussi tu détermines la valeur maximale sur l'intervalle
- ce qui te permet d'identifier le a dans le dernier intervalle
- trace toutes ces parties sur le plan cartésien et comme tu connais les valeurs cela te permet de mieux identifier tes échelles de valeurs pour l'axe des x et des y ( t et P)
- tu sais sur quel intervalle le maximum de 30000 poIssons sera atteint (quand 15 t² = 30000 )
- trouve t
Re: Question
Salut 😁
Merci pour ta question!
Sur cette fiche, tu trouveras toutes les techniques d'un passage d'une forme à l'autre.
Pour passer de la forme canonique à la forme générale, il suffit de développer de façon algébrique l’équation de la fonction.
En voici un exemple.
Pour passer de la forme générale à la forme canonique, on doit trouver les valeurs des paramètres h et k: a reste le même.
En voici un exemple.
N'hésite pas si tu as d'autres questions 😊
À bientôt 😎
Re: Question
Bonjour!
L’extremum et l’image donnent tous deux les mêmes informations.
Cependant, l’extrémum et l’image ont des notations différentes pour exprimer les mêmes données.
Prenons comme exemple une fonction dont le maximum est 10 et où il n’y a pas de minimum.
Si on l’écrit selon la notion de l’extremum, on le noterait de la façon suivante:
Min: Aucun
Max: 10
Cependant, si on l’écrit selon l’image, on la noterait de la façon suivante :
y e ]-infini, 10]
ou
f(x) e ]-infini, 10]
J’espère que ça t’as aidé!
Question
Salut allôprof!
Est-ce que vous savez quelle est la différence entre l'extrémum et l'image d'une fonction, concernant les propriétés d'une fonction?
Merci beaucoup!
Re: Question
Salut CitrouilleBionique5879 😁
Merci pour ta question!
Évaporation
Vapeur et résidu solide
Filtration
Filtrat et résidu
Distillation
Distillat et résidu
Tamisage
Particules fines et particules grossières
Centrifugation
Surnageant et précipité
Décantation
Décantat (ou surnageant) et Sédiment
N'hésite pas si tu as d'autres questions 😊
À bientôt 😎
Question
Encore bonjour!
Cette fois-ci, j'avais besoin de votre aide sur les changements de vitesse.
En fait, j'ai beaucoup de difficultés à bien interpréter les rapports de vitesse et de dire quel organe (menant ou mené est x fois plus lent ou x fois plus rapide que l'autre).
En fait, si je suis votre formule de rapport de vitesse:
Mettons que j'ai deux roues dentées. L'organe menant est la petite roue dentée (ayant 16 dents) et l'organe mené est la grande roue dentée (ayant 24 dents). Si je fais le rapport, j'obtiens 16/24 = 0,66666666666666666 ou 2/3. C'est ici que ça me pose problème, je ne sais plus comment l'interpréter. Est-ce que je dis que la grande roue dentée tourne 2/3 fois moins vite que la petite roue dentée ? Personnellement, la manière dont moi je le vois c'est que pour 16 dents, la grande roue dentée a fait 2/3 tour. Mais, je ne sais pas comment interpréter le nombre de fois...
Un autre exemple:
Mettons que la grande roue dentée est l'organe menant et a 24 dents, alors que la petite roue dentée est l'organe mené, ayant 16 dents.
Si je fais le rapport, ça me donne 24/16 = 1,5. Qu'est-ce que ça veut dire par rapport au nombre de fois: est-ce que la petite roue tourne 1,5 fois plus rapidement que la grande ou je dis que la grande tourne 1,5 fois moins vite que la petite ?
Svp aidez-moi, je sais que cela et énorme comme question, mais je veux bien réussir mon année :_(
Merci :D