Best Of

Bonjour CitrineDelta9900,

Dans ce problème de mathématiques, tu dois trouver le périmètre d'un des quadrilatères dans les coins du musée, mais je suis sûr que tu le sais déjà.

Décodons cette situation ensemble. Premièrement, il faut savoir que les données que tu as ici ne sont pas toutes en mètres, donc il faudra convertir ces dernières :

-Le périmètre du pentagone extérieur est de 14,25 hectomètres, ce qui donne 1425 mètres.

-Le périmètre du pentagone représentant la cour est de p 0.575 km, ce qui donne 575 mètres.

-Le périmètre d'un des 5 rectangles est de 45 000 cm, ce qui donne 450 mètres.

Ensuite, il est enfin temps de connaître le périmètre de cette figure. Un côté du mur extérieur mesure 285 mètres, issu de 1425 divisé par 5. Un côté du pentagone intérieur mesure 115 mètres, issu de 575 divisé par 5, qui veut dire qu'on a déjà la mesure des longueurs du rectangle. Sachant que les longueurs du rectangle réunies mesurent ensemble 115+115, cela fait 230 mètres. Donc, les largeurs du rectangle mesurent ensemble 450-230, qui donne 220, voulant dire que chaque côté de largeur représente 110 mètres.

Maintenant, 285 (côté du grand rectangle) moins 115 (longueur du rectangle) donne 170, qu'on peut considérer comme les deux petits côtés du quadrilatère isocèle. Et pour trouver les deux plus longs, on a juste à doubler la valeur de la largeur du rectangle, soit 110 x 2, qui donne 220.

Finalement, le périmètre du quadrilatère isocèle est de 220 + 170 qui donne 390 mètres.

Pour plus d'informations, je t'invite à jeter un coup d'œil au fiches d'Alloprof.

Sur ce, je te souhaite une bonne journée.

"Si je comprends bien à la question 2 b) c'est 82 sixième. Si je le divise ça ne fait pas 12 mais 13,6666..."

Tu as tout à fait raison c'est bien 13.666... c'est mon erreur!!

82/6 = (78 + 4)/6 = 13 + 4/6 = 13 4/6

Tel que mentionné chaque petite unité sur la droite représente 1/6 donc ton point sera placé 4 unités plus loin que 13.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

"Puis là question 3, je ne comprend pas je dois faire ? ÷ 6 = 12."

Tu veux connaître la valeur à placer aux ... que j'ai remplacé par un ? mais qu'on peut remplacer par un x pour le numérateur inconnu de la fraction.

Tu cherches le x tel que

x/6 = 12

en multipliant par 6 des deux côtés (pour maintenir l'égalité) on a

x = 6 · 12 = 72

J'espère que c'est plus clair.

Désolée.

Salut !

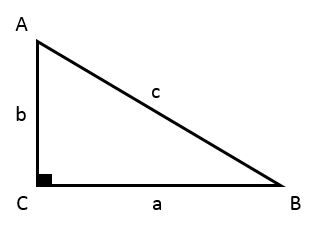
Merci de faire appel au service d'Alloprof ! es rapports trigonométriques dans le triangle rectangle expriment un rapport entre les longueurs de deux côtés.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

$$ \begin{align} \sin A &= \dfrac{\text{mesure de la cathète opposée à l'angle A}}{\text{mesure de l'hypoténuse}}\\ &= \dfrac{a}{c}\\\\ \cos A &= \dfrac{\text{mesure de la cathète adjacente à l'angle A}}{\text{mesure de l'hypoténuse}} \\ &= \dfrac{b}{c}\\\\ \tan A &= \dfrac{\text{mesure de la cathète opposée à l'angle A}}{\text{mesure de la cathète adjacente à l'angle A}} \\ &= \dfrac{a}{b}\end{align} $$

Pour chacun des triangles, on te donne au moins un des ratios, ce qui tonne au moins deux mesures par triangles te permettant de trouver l'autre angle et l'autre mesure. Par exemple, en a), l'hypoténuse est 59 et le côté opposé est 22.

J'espère que cette explication ait pu t'aider et si tu as d'autres questions, n'hésite pas !

Bonne soirée !