Best Of
Re: Question
Bonjour CibouletteBionique995,
Merci d'avoir utilisé la zone d'entraide.
Dans ce cas, tu dois mettre un s à désagréables, puisqu'il s'accord avec "effets" et c'est un adjectif, une classe de mots variable.
Tu peux te renseigner plus sur ce sujet dans la fiche suivante:
Bonne étude!
BrontosaureSigma5635
Re: Question
peu que ma réponse ne t’aide pas mais pour les apprendre moi je me fais une feuille et je les écris mais à chaque verbe différent je laisse une partie vide et j’étudie un peu et j’essaye de compléter je n’arrive pas beaucoup à expliquer mais j’espère que ça pourra t’aider un peut
Re: Question
Bonjour MarsRouge,
Merci de faire appel à nos services! :)
En fait, le futur antérieur sert souvent à exprimer un fait qui sera terminé avant un autre (exprimé au futur simple) dans le futur.
Ex. :
1. Quand j'aurai terminé ce projet, je prendrai des vacances.
2. Quand elle aura fini ses études, elle partira en Angleterre.
N'hésite pas à nous réécrire si tu as d'autres questions! :)
Marilee
Re: Question
Bonjour, ScorpionTurquoise1022.
Merci d'avoir utilisé la zone d'entraide.
Pour écrire un roman, voici 4 étapes;
1.Tout d'abord, trouve toi un thème pour ton histoire. Ton histoire peut aborder le sujet d'horreur psychologique, l'aventure fantastique ou même l'amour.
2.Ensuite, planifie ton histoire en plaçant ses événements dans un ordre chronologique. Ton travail devrait habituellement contenir une introduction (situation initiale), un élément déclencheur, un déroulement, un dénouement et une situation finale.
3.Pour poursuivre, réalise des personnages qui soutiendront ton histoire. Cependant, assure toi de décrire des individus réalistes, crédibles et surtout uniques. Cela rends ton histoire riche et intrigante. Pour effectuer cela, tu peux t'inspirer de personnalités provenant de tes émissions de télévision ou livres préférés.
4.En conclusion, lorsque tu auras accompli toutes ces étapes, tu pourras enfin écrire ton histoire sur un papier brouillon pour ensuite la corriger et effacer les erreurs et la réécrire au propre.
Voici un lien pour t'aider: Trucs pour la correction d'un texte | Secondaire | Alloprof
N'hésite pas à poser des questions de nouveaux,
Bonne continuation,
Re: Question
Bonjour !
En rajoutant sur ce que RubiArtistique a dit , je t'invite à essayer de faire tout tes devoirs !. Si tu as de la difficulté ou si tu bloques, tu peux demander à tes collègues de classe, à ton professeur et même à Alloprof de l'aide ! Je t'invite aussi à aller aux récupérations offertes par ton enseignant :) . Finalement, nous avons aussi une ligne téléphonique, alors si tu veux, tu peux appeler Alloprof pour de l'aide par téléphone !
n'hésite pas si tu as questions :)
VC
Re: Question
Met toi a un bon endroit pour travaille comme ca tu seras concentrer, place tes affaires, prend toi un verre d'eau, met toi de la musique et tout se que tu auras a faire ce sera de trouver la volonter.
Re: Question
Salut!
Pour résoudre une équation et trouver l'inconnu, tu dois toujours placer les termes semblables d'un côté de l'équation, et les constantes de l'autre côté. Prenons un exemple pour mieux comprendre.
On a l'équation :
$$ 4x - 6 = 2x + 10$$
Les termes semblables sont les termes ayant les mêmes variables (les mêmes inconnus), et ces variables sont affectées des mêmes exposants. Donc, nos termes semblables sont ici \(4x \) et \( 2x\), puisqu'ils contiennent tous les deux la variable x affectée d'un exposant 1.
Les constantes sont les termes qui ne contiennent pas de variables, soit ici \(-6\) et \(10\).
Notre but sera d'abord de placer d'un côté de l'égalité les deux termes semblables, et de l'autre côté les constantes. Pour ce faire, nous allons commencer par déplacer un des deux termes semblables de l'autre côté (peu importe lequel), et ce, en effectuant l'opération inverse.
Déplaçons \(2x\) du côté gauche de l'égalité. Puisque l'opération inverse d'une addition est une soustraction, nous allons devoir soustraire \( 2x\) de chaque côté de l'équation, comme ceci :
$$ 4x - 6 -2x= 2x + 10-2x$$
En le soustrayant de chaque côté, cela nous permet de l'éliminer du côté droit de l'équation :
$$ 4x - 6 -2x= 10$$
On a ainsi déplacé le terme \(2x\) afin qu'il soit du même côté que son terme semblable.
Passons maintenant aux constantes. Nous allons déplacer la constante \(6\) de l'autre côté. Puisque l'opération inverse d'une soustraction est une addition, nous allons donc additionner \(6\) de chaque côté :
$$ 4x - 6 -2x+6= 10+6$$
$$ 4x -2x= 10+6$$
On a ainsi réussi à placer nos termes semblables d'un côté et nos constantes de l'autre! La prochaine étape sera d'additionner les constantes, et d'additionner les coefficients des termes semblables. Commençons par les constantes. Puisque 10+6 donne 16, nous avons :
$$ 4x -2x= 16$$
Pour soustraire les termes semblables, il faut soustraire leur coefficient, c'est-à-dire le nombre devant la variable x.
$$ (4-2)x= 16$$
$$ 2x= 16$$
Finalement, la dernière étape sera d'éliminer le coefficient de la variable x, soit \(2\), et ce, en effectuant l'opération inverse d'une multiplication, soit une division :
$$ \frac{2x}{2} = \frac{16}{2} $$
$$x=8$$
Voilà!
Une fois que tu as résolu l'équation, tu peux valider si ton résultat est bon en remplaçant x par la valeur trouvée dans l'équation initiale, puis en vérifiant si tu obtiens le même résultat des deux côtés de l'égalité.
$$ 4x - 6 = 2x + 10$$
$$ 4(8) - 6 = 2(8) + 10$$
$$ 32 - 6 = 16 + 10$$
$$ 26 = 26$$
On a le même résultat des deux côtés de l'égalité, l'équation est donc juste et nous pouvons confirmer que notre réponse, soit x=8, est la bonne!
Voici des fiches sur ces notions qui pourraient t'être utiles :
- La résolution d'équations et d'inéquations | Secondaire | Alloprof
- Algèbre - Expressions algébriques | Alloprof
Voici la résolution du numéro 1) :
$$ \frac{92}{14}+a=\frac{3}{7}$$
On déplace la constante 92/14 de l'autre côté de l'équation :
$$ \frac{92}{14}+a- \frac{92}{14}=\frac{3}{7}- \frac{92}{14}$$
$$ a=\frac{3}{7}- \frac{92}{14}$$
On effectue la soustraction de fraction. Pour cela, on commence par placer nos fractions sur le même dénominateur :
$$ a=\frac{3\times 2}{7\times 2}- \frac{92}{14}$$
$$ a=\frac{6}{14}- \frac{92}{14}$$
$$ a= \frac{6-92}{14}$$
$$ a= \frac{-86}{14}$$
Finalement, on réduit la fraction pour avoir une fraction irréductible :
$$ a= \frac{-86\div 2}{14\div 2}$$
$$ a= \frac{-43}{7}$$
Voici la résolution du numéro 2) :
$$ b \div \frac{3}{4} = \frac{8}{7}$$
On déplace la constante 3/4 de l'autre côté de l'équation afin d'isoler la variable b, et ce, en effectuant l'opération inverse d'une division, soit une multiplication :
$$ b \div \frac{3}{4} \times \frac{3}{4} = \frac{8}{7} \times \frac{3}{4} $$
$$ b = \frac{8}{7} \times \frac{3}{4} $$
On effectue la multiplication de fraction en multipliant les numérateurs ensemble et les dénominateurs ensemble :
$$ b = \frac{8 \times 3}{7 \times 4}$$
$$ b = \frac{24}{28}$$
On réduit la fraction en divisant par le PGCD de 24 et 28 :
$$ b = \frac{24 \div 4}{28 \div 4}$$
$$ b = \frac{6}{7}$$
Voici la résolution du numéro 3) :
$$ \frac{b}{7} = \frac{3}{4} $$
On déplace la constante 7 en effectuant l'opération inverse d'une division par 7, soit une multiplication par 7 :
$$ \frac{b}{7} \times 7= \frac{3}{4} \times 7$$
$$b= \frac{3}{4} \times 7$$
On multiplie les fractions :
$$b= \frac{3}{4} \times \frac{7}{1}$$
$$b= \frac{3\times 7}{4\times 1} $$
$$b= \frac{21}{4} $$
Alternativement, on peut effectuer un produit croisé pour résoudre cette équation, c'est-à-dire qu'on multiplie les nombres en diagonale et on divise par le nombre restant : \(b = 3 \times 7 \div 4 = 21 \div 4 = \frac{21}{4} \)
Voici la résolution du numéro 4) :
$$ \frac{(b-5)}{7}=\frac{3}{4}$$
On commence par détruire la fraction contenant la variable b en multipliant chaque côté par le dénominateur 7 :
$$ \frac{(b-5)}{7} \times 7=\frac{3}{4} \times 7$$
$$ (b-5)=\frac{3}{4} \times 7$$
$$ b-5=\frac{3}{4} \times \frac{7}{1}$$
$$ b-5=\frac{3\times 7}{4\times 1}$$
$$ b-5=\frac{21}{4}$$
On déplace la constante 5 en effectuant l'opération inverse d'une soustraction par 5, soit une addition par 5 :
$$ b-5+5=\frac{21}{4}+5$$
$$ b=\frac{21}{4}+5$$
On effectue l'addition de fraction :
$$ b=\frac{21}{4}+\frac{5}{1}$$
$$ b=\frac{21}{4}+\frac{5\times 4}{1\times 4}$$
$$ b=\frac{21}{4}+\frac{20}{4}$$
$$ b=\frac{21+20}{4}$$
$$ b=\frac{41}{4}$$
Voici la résolution du numéro 5) :
$$ \frac{-64}{24}-(\frac{-30}{45}+c)=\frac{2}{3}$$
On peut commencer par distribuer le signe négatif sur chaque terme dans les parenthèses afin d'éliminer ces parenthèses :
$$ \frac{-64}{24}-\frac{-30}{45}-c=\frac{2}{3}$$
Lorsqu'on a deux signes négatifs consécutifs, cela équivaut à une addition (--30/45 = 30/45):
$$ \frac{-64}{24}+\frac{30}{45}-c=\frac{2}{3}$$
On déplace nos termes -64/24 et 30/45 de l'autre côté de l'équation en effectuant les opérations inverses :
$$ \frac{-64}{24}+\frac{30}{45}-c+\frac{64}{24}=\frac{2}{3}+\frac{64}{24}$$
$$ \frac{30}{45}-c=\frac{2}{3}+\frac{64}{24}$$
$$ \frac{30}{45}-c -\frac{30}{45} =\frac{2}{3}+\frac{64}{24} - \frac{30}{45}$$
$$-c =\frac{2}{3}+\frac{64}{24} - \frac{30}{45}$$
Pour effectuer cette addition et soustraction de fraction, on peut commencer par réduire nos fractions :
$$-c =\frac{2}{3}+\frac{64\div 8}{24\div 8} - \frac{30\div15}{45 \div15} $$
$$-c =\frac{2}{3}+\frac{8}{3} - \frac{2}{3} $$
$$-c =\frac{2+8-2}{3} $$
$$-c =\frac{8}{3} $$
Finalement, on divise chaque côté par -1 afin d'éliminer le signe négatif de la variable c (l'opération inverse d'une multiplication par -1 est une division par -1) :
$$c =-\frac{8}{3} $$
J'espère que c'est plus clair pour toi! Sinon, n'hésite pas à nous réécrire! :)
Bon succès pour ton examen! 😁
PS Si tu as un appareil mobile ou une tablette, tu peux utiliser l'application Photomath pour t'aider dans tes résolutions d'équations!
Re: Question
Salut!
Pour le premier numéro, pour convertir les nombres donnés dans des bases différentes en base 10, il faut utiliser la valeur positionnelle.
Le nombre 425 en base 10 peut se décomposer comme ceci :
$$5 = 5 × 10^0$$
$$20 = 2 × 10^1$$
$$400 = 4 × 10^2$$
En additionnant le tout, on obtient notre nombre de départ : 400 + 20 + 5 = 425
Ainsi, pour décomposer n'importe quel nombre, on peut trouver la valeur de chaque chiffre composant ce nombre, puis additionner toutes les valeurs. Pour trouver la valeur d'un chiffre dans un nombre, on suit cette formule :
$$ valeur~du~chiffre~dans~le~nombre = chiffre \times base^{position~du~chiffre} $$
d'où \(425 =(4 \times 10^2) + (2 \times 10^1) + (5 \times 10^0)\), puisqu'on est en base 10.
Super important, on commence à compter les positions des chiffres à partir de 0, et non 1. En d'autres mots, le chiffre 5 dans le nombre 425 est à la position 0, le chiffre 2 est à la position 1, et le chiffre 4 est à la position 2.
En suivant ce principe, on peut convertir un nombre dans une autre base en un nombre en base 10. Voici comment faire pour chaque nombre :
$$ 325_{(6)}$$
Le nombre 325 en base 6 peut se décomposer comme ceci :
$$ 3 \times 6^2 $$
$$2 \times 6^1 $$
$$5 \times 6^0$$
En additionnant le tout, on obtient le nombre équivalent en base 10 :
$$ 325_{(6)} = [(3 \times 6^2 ) + (2 \times 6^1) + (5 \times 6^0)]_{(10)}$$
$$ 325_{(6)} = [(108) + (12) + (5)]_{(10)}$$
$$ 325_{(6)} = 125_{(10)}$$
------------------
$$ 1258_{(9)}$$
Le nombre 1258 en base 9 peut se décomposer comme ceci :
$$ 1 \times 9^3 $$
$$ 2 \times 9^2 $$
$$5\times 9^1 $$
$$8 \times 9^0$$
En additionnant le tout, on obtient le nombre équivalent en base 10 :
$$ 1258_{(9)} = [(1 \times 9^3 ) +(2 \times 9^2 ) + (5 \times 9^1) + (8 \times 9^0)]_{(10)}$$
$$ 1258_{(9)} = [(729) + (162) + (45) + (8)]_{(10)}$$
$$ 1258_{(9)}= 944_{(10)}$$
------------------
$$ 38541_{(5)}$$
Il y a une erreur dans ce numéro! Il est impossible d'avoir le nombre 38541 en base 5, puisque dans cette base, seuls les chiffres 0, 1, 2, 3 et 4 existent. Il n'existe pas de chiffre 5 ni de chiffre 8 en base 5.
Le nombre 38541 n'existe donc pas pour une base 5, ni pour une base 6, ni pour la 7, ni pour la 8. Il peut seulement exister pour une base 9 et plus.
Concernant le second numéro, nous devons utiliser la méthode de la division successive.
$$625_{(10)}$$
On divise 625 par 4 successivement, et le reste de chaque division nous donnera les chiffres composant le nombre en base 4 :
$$ 625 \div 4 = 156 ~reste~1 $$
$$ 156 \div 4 = 39 ~reste~0 $$
$$ 39 \div 4 = 9 ~reste~3 $$
$$ 9 \div 4 = 2 ~reste~1 $$
$$ 2 \div 4 = 0 ~reste~2 $$
Donc, 625 en base 10 est équivalent à 21301 en base 4.
$$ 625_{(10)}=21301 _{(4)}$$
--------------
$$3245_{(10)}$$
On divise 3245 par 8 successivement, et le reste de chaque division nous donnera les chiffres composant le nombre en base 8 :
$$ 3245 \div 8 = 405 ~reste~5 $$
$$ 405 \div 8 = 50 ~reste~5 $$
$$ 50 \div 8 = 6 ~reste~2 $$
$$ 6 \div 8 = 0 ~reste~6 $$
Donc, 3245 en base 10 est équivalent à 6255 en base 8.
$$ 3245_{(10)}= 6255_{(8)}$$
Pour convertir les nombres \(5421_{(6)}\) et \(322_{(4)}\) en base 5, tu dois commencer par les convertir en base 10 en utilisant la méthode de la valeur des positions décrite au premier numéro, puis tu pourras alors les convertir en base 5 à l'aide de la méthode de la division successive décrite dans ce second numéro. Tu peux ensuite vérifier tes réponses obtenues à l'aide de ce site : Convertisseuse de base
Voici une fiche sur cette notion qui pourrait t'être utile : Les systèmes de numération | Secondaire | Alloprof
J'espère que cela t'aide! :)
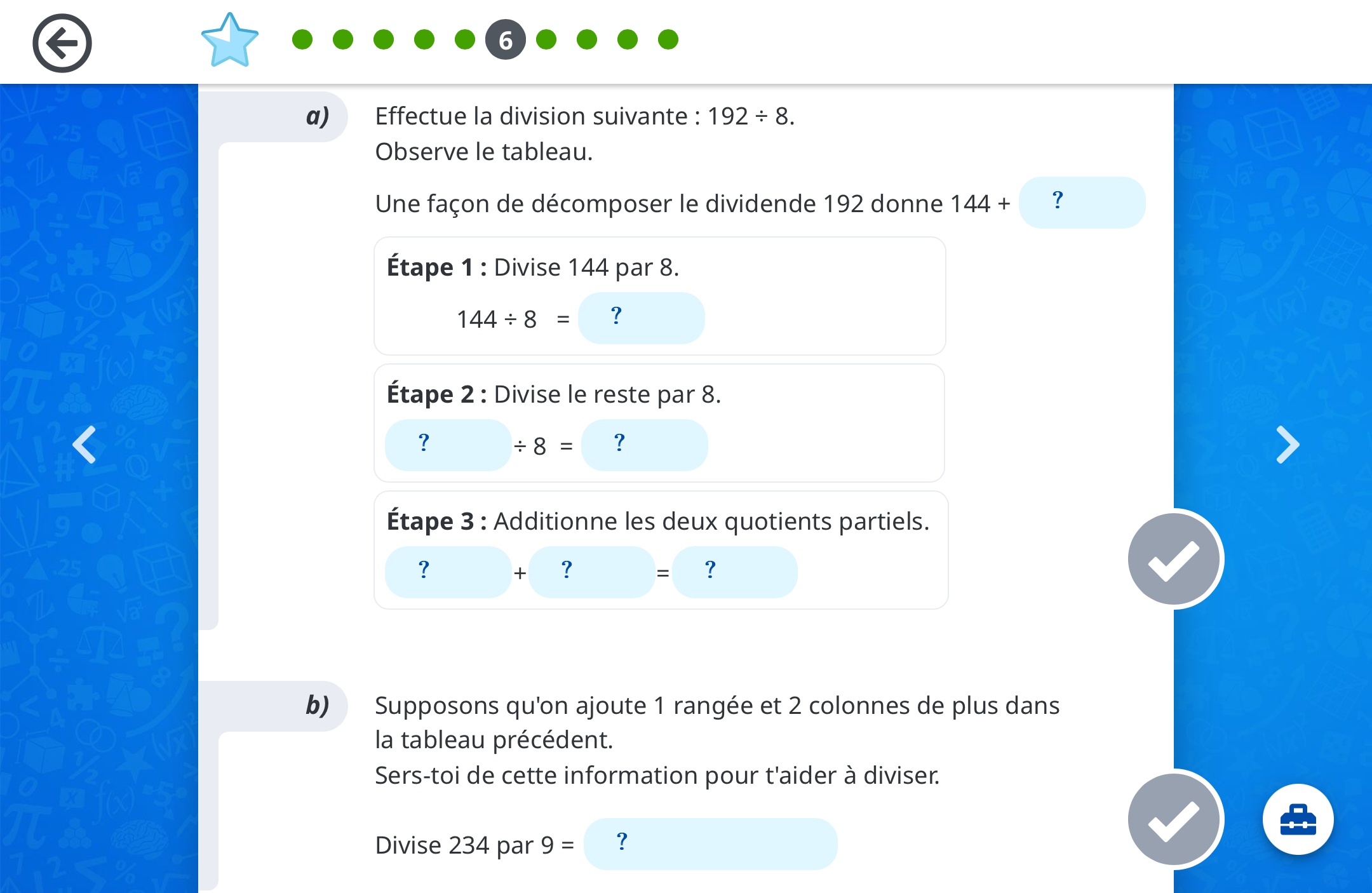
Question
Salut ! Il ne me reste que cet exercice dans netmath pour jeudi ! Aidez moi avec la démarche, je ne sais pas quoi faire. J’aimerais que vous me répondiez ce soir ou demain juste pour en finir avec. Merci beaucoup Katia K et les autres profs !