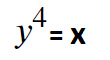Best Of
Re: Question
Rebonjour ! :) Par ta question, je crois que tu es un élève postsecondaire...
Je ne dirais pas qu'il y a des placements «trop audacieux», en soi. Certains sont toutefois trop audacieux pour ton mode de vie/tes moyens.
Ce genre de placement consiste souvent à investir dans quelque chose plus «à risque» (plus volatile), dont la valeur est moins stable. Cela peut aussi être un investissement en lien avec un événement (IPO, merge etc) qui pourrait avoir un gros impact.
Ces investissements ont pour risque de te faire perdre de l'argent rapidement (chute du prix drastique). En même temps, ils ont autant le risque de te faire gagner de l'argent rapidement.
Au contraire, les fonds de placements ou les placements à revenus garantis te donneront un revenu plus petit, mais il y aura moins de risque de pertes.
J'espère que ça répond à ta question ! :) N'hésite pas à contacter un conseiller en placements (banque) si tu as des questions plus précises en lien avec tes propres investissements ! :D
Sarah G
Re: Question
Rebonjour ! :) Merci de faire appel à nos services !
Tu trouveras quelques conseils pour épargner aux liens suivants :
Je t'invite à te planifier un budget pour comprendre quelles sont tes dépenses et comment tu peux épargner. Tu pourrais notamment prendre un montant de ta paye par mois, y aller par % si tu n'as pas un revenu stable, te donner un objectif annuel fixe que tu diviseras selon ton revenu, etc.
Pour plus d'infos, c'est juste ici : https://www.alloprof.qc.ca/fr/eleves/bv/education-financiere/le-budget-personnel-h1821
À ta prochaine question ! ;)
Sarah G
Re: Question
Bonjour ! :) Merci pour ta question !
Le fond commun de placement fait en sorte que plusieurs actionnaires investissent dans un fond qui regroupe plusieurs compagnies. Ce sont des gestionnaires/banquiers qui s'occupent d'investir dans différents fonds.
Puisqu'il s'agit d'un regroupement, l'argent investie est divisée d'avantage et est donc moins à risque (si la cote d'une compagnie chute, il se peut que la valeur du fond reste stable si une autre augmente). Par contre, l'intérêt est souvent plus bas que celui que l'on pourrait faire avec des actions individuelles (notamment certains «pennystock», qui sont extrêmement volatiles et peuvent augmenter de 20% en quelques minutes).
N'hésite pas si tu as d'autres questions ! :D
Sarah G
Re: Question
Tu peux l'appliquer, il faut juste faire un changement de variable
L'expression devient
x²-8x-128 on peut la factoriser en x
puis dans le résultat final, tu remplaces x par y puissance 4
Re: Question
Bonjour!
Les notions à réviser sont les notions de la 4e, 5e année et 6e année, bref les années du primaires! Dans les répertoires de révision que nous t'avons conseillé, il y a les notions que tu dois maîtriser pour l'examen d'entrée.
Je te suggère donc de regarder les notions dans les répertoires et réviser celles que tu connais moins bien. Concentre-toi sur les notions que tu comprends moins pour ne pas avoir de mauvaises surprises à l'examen! :)
Si tu as d'autres questions, n'hésite pas à nous réécrire. Nous te répondrons avec plaisir!
Laurie :)
Re: Question
Bonjour,
Pour cela il faut au moins être au secondaire.
Désolé
Bonne journée :)
Re: Question
Bonjour TigreAutonome,
Merci de faire appel à nos services! :)
Déclarer une faillite est une mesure extrême et entraîne nécessairement des conséquences à long terme sur la vie financière. Avant de prendre cette décision, une personne peut contacter ses créanciers afin de discuter avec eux de ses difficultés financières. Certains créanciers peuvent élaborer un plan de remboursement des dettes qui est plus abordable.
Une autre solution peut être d'établir un budget réaliste qui permet de rembourser les dettes.
Enfin, si une personne a plusieurs dettes, il est parfois possible de les consolider (les regrouper), ce qui simplifie les paiements et pourrait même entraîner une réduction des taux d'intérêt.
N'hésite pas à nous réécrire si tu as d'autres questions! :)
Marilee
Re: Question
Bonjour TigreAutonome,
Merci de faire appel à nos services! :)
Changer le taux d'intérêt aurait nécessairement des impacts sur le paiement à faire chaque mois. Les paiements seront plus élevés avec un taux de 6% qu'un taux de 4%.
Si tu souhaites calculer la différence de paiement entre ces deux taux, je t'invite à consulter la fiche suivante :
N'hésite pas à nous réécrire si tu as d'autres questions! :)
Marilee
Re: Question
Bonjour TigreAutonome,
Merci de faire appel à nos services! :)
Il peut y avoir plusieurs signes associés aux défis financiers, en voici quelques-uns qui sont fréquents :
- Difficultés à payer les factures à temps;
- Avoir recours de manières répétées aux cartes de crédit pour couvrir les dépenses courantes;
- Demandes fréquentes de prêts financiers;
- Réduire les dépenses essentielles (nourritures, soin de santé, etc.);
- L'incapacité à épargner;
- Anxiété liée aux dépenses;
- etc.
N'hésite pas à nous réécrire si tu as d'autres questions! :)
Marilee
Re: Question
Salut!
Si on remplace la variable \(a\) par \(x\), on obtient la forme suivante :
$$ a^2 -51ab+50b^2 $$
$$ x^2 -51xb+50b^2 $$
On peut ensuite réécrire notre expression pour identifier les différents paramètres :
$$ x^2 -51xb+50b^2 $$
$$ 1x^2 +(-51b)x+50b^2 $$
Ce qui équivaut ainsi à la forme \(Ax^2+Bx+C\).
En d'autres mots, la variable \(a\) dans le trinôme \(a^2 -51ab+50b^2\) agit comme la variable \(x\) dans \(Ax^2+Bx+C\), et la variable \(b\) dans \(a^2 -51ab+50b^2\) doit être traitée comme une simple constante.
Nos paramètres A, B et C de la forme \(Ax^2+Bx+C\) sont donc \(A = 1\), \(B = -51b\) et \(C = 50b^2\).
Nous allons alors chercher deux nombres \(m\) et \(n\) dont le produit est :
$$ produit = AC = 1 \times 50b^2 =50b^2 $$
et dont la somme est :
$$ somme = B = -51b$$
Ces nombres sont \(m=-b\) et \(n=-50b\), car leur produit est :
$$ -b \times -50b = 50b^2 $$
et leur somme est :
$$ -b + -50b = -51b$$
Nous allons maintenant décomposer le second terme de notre trinôme par les deux nombres trouvés :
$$ a^2 -51ab+50b^2 $$
$$ a^2 -ab-50ab+50b^2 $$
Pour finir, il faut effectuer une mise en évidence double.
J'espère que c'est plus clair pour toi! Si tu as de la difficulté à terminer la factorisation ou si tu as d'autres questions, n'hésite pas à nous réécrire :)