Best Of
Re: Question
Allo Paruline Rose,
J'ai penser a ça :
ait utilisEncore un effort et je dirais bientôt mon discourt devant les acclamations et les applaudissements de la foule.
Il y a trois mots de la liste qui n'on pas utilisé: effort, acclamation et applaudissement.
Et un verbe au conditionnel ( dire )
J'espère t'avoir aidé !
Bonne chance !
Re: Question
Bonjour ParulineRose3048,
Merci d'avoir utilisé alloprof pour répondre à ta question!
Tu pourrais utiliser les mots une apparition et un effroi, ainsi que le verbe apercevoir au conditionel.
J'espère que ça t'aide!
N'hésite pas à nous poser d'autres questions.
Continue comme ça!
LoupAlpha4506
Re: Question
Bonsoir, CentaureVolubile6818,
Merci de solliciter nos services.
Afin de trouver la réponse à ta question, je t’invite à jeter un coup d’oeil à la fiche explicative ci-dessous.
N’hésite pas à nous réécrire, si tu as d’autres questions ou si tu as besoin de précisions!
Émilie
Re: Question
Bonsoir, CobraGrandiose3942,
Merci de solliciter nos services.
Quels genres de problèmes cherches-tu? Des additions d’expressions algébriques, des soustractions, des multiplications?
Bref, je t’invite à cliquer sur le lien ci-dessous afin d’accéder à tous les exercices de notre site. À partir de cette page, tu pourras trouver le genre d’exercice qui conviendra le mieux à tes besoins.
Si tu ne trouves, n’hésite pas à nous réécrire en nous précisant exactement ce que tu recherches.
À bientôt !
Émilie
Re: Question
Salut!
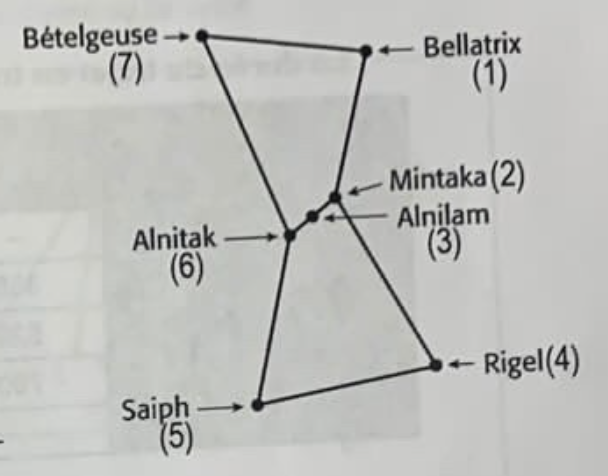
Concernant le numéro 3, dans un graphe, une arête est une ligne reliant des sommets. À la question b), on te demande de trouver un chemin débutant à l'étoile 7 et permettant de traverser toutes les étoiles. Or, on veut que la chaîne soit simple, c'est-à-dire qu'il ne passe pas plusieurs fois sur la même étoile. Par exemple, la chaîne 7-6-5-4-2-1-2-3 permet de passer par toutes les étoiles, mais n'est pas la chaîne la plus simple, puisqu'on passe deux fois que l'étoile 2.
Ensuite, on te demande de trouver un cycle, c'est-à-dire un chemin débutant et revenant à l'étoile 7. Par exemple, 7-6-3-2-1-7 est un cycle, tout comme 7-6-5-4-2-3-6-7 ou encore 7-6-7. Or, on te demande de trouver le plus long cycle possible qui ne passe pas plus d'une fois par la même arête.
Pour le numéro 4, le degré d'un sommet dans un graphe est le nombre d'arêtes incidentes à ce sommet. Par exemple, le degré du sommet de l'étoile Alnitak est de 3, puisqu'il est connecté à trois arêtes.
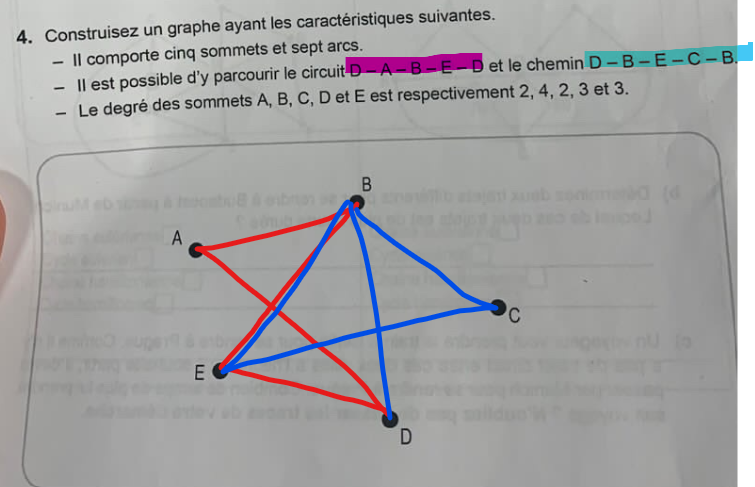
Pour construire ton graphique, tu dois commencer par tracer le circuit (cycle) D-A-B-E-D et le chemin D-B-E-C-B :
Tu peux ensuite vérifier que les autres conditions sont bien respectées.
J'espère que c'est plus clair pour toi! :)
Re: Question
Salut!
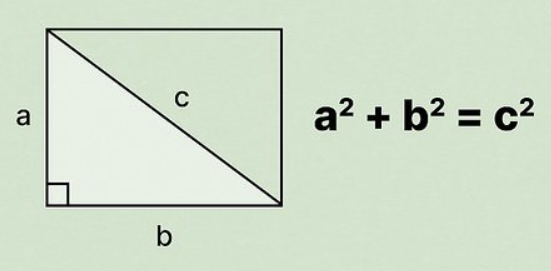
Tu dois utiliser le théorème de Pythagore pour résoudre ce problème.
On sait que la diagonale mesure 40 cm. La diagonale du rectangle est aussi l'hypoténuse du triangle rectangle formé par la diagonale, la hauteur et la base du rectangle. On a donc l'équation suivante :
$$ 40^2 = a^2 + b^2 $$
On nous dit également que la hauteur est le triple de la base. Si nous posons la variable \(x\) comme étant la mesure de la base, alors la hauteur serait de \(3x\) cm. En insérant ces expressions dans notre équation de Pythagore, nous avons :
$$ 40^2 = (3x)^2 + x^2 $$
Tu es alors en mesure de résoudre cette équation pour trouver x, la mesure de la base du rectangle.
Je te laisse terminer avec ces indices. J'espère que c'est plus clair pour toi! :)
Re: Question
Salut MentheTurquoise553!
Merci d'avoir utilisé la zone d'entraide.
D'abord, tu dois trouver le taux de variation "a" des fonctions. Par exemple, le taux de variation du premier énoncé est 3. N'oublie pas que y = ax+b.
Je t'invite à consulter la fiche suivante pour plus de précisions:
J'espère que cela répond à ta question!
Bon travail :)
PoivronRouge571
Re: Question
Bonjour CyborgIntergalactique,
Merci de faire appel à nos services! :)
Voici les différentes étapes de la démarche scientifique :
N'hésite pas à nous réécrire si tu as d'autres questions! :)
Marilee
Re: Question
Bonsoir, JujubeMauve9839,
Merci de solliciter nos services.
Tout d’abord, tu connais déjà deux niveaux de subdivision sur sept. Les cinq autres, tout comme les espèces, permettent d’associer chacune des espèces à de plus grandes familles.
Personnellement, j’aime bien imager les taxons en utilisant les adresses postales pour un extraterrestre. En premier lieu, le règne peut être comparé à la planète, l’embranchement au continent, la classe au pays, l’ordre à la province, la famille à la ville, le genre à la rue et l’espèce au numéro de porte.
Le règne part de l’information la plus large et de plus en plus nous utilisons des informations pour viser spécifiquement une maison, une espèce dans le cas des vivants.
Cela étant dit, je t’invite à cliquer sur le lien ci-dessous afin d’en apprendre davantage concernant la taxonomie et son fonctionnement.
En espérant que ma réponse t’aide un petit peu!
Émilie
Re: Question
Bonjour TatooineBeta,
Merci pour ta question!
Tu dois d'abord de demander si l'énergie doit se trouver du côté des réactifs (l'énergie est absorbée par la réaction) ou des produits (l'énergie est dégagée par la réaction). Ici, il est dit que la réaction "nécessite" l'énergie, qu'elle en a donc besoin.
Ensuite, tu peux trouver la valeur de cette énergie en calculant le nombre de moles correspondant à 1 g de NO, puis en divisant 1732,8 J par ce nombre de moles pour trouver l'enthalpie de réaction par mole.
N'hésite pas si tu as encore besoin d'aide:)
Kylan