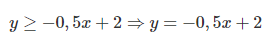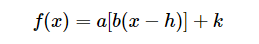Best Of

Bonjour SaturneKappa473,

Pour tracer cette inéquation, il faut:

1) changer ton inéquation en équation:

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

2) faire une table de valeurs avec ton équation y=-0,5x +2 pour placer tes points dans le plan cartésien (tu choisis les valeurs de x)

3) analyser ton symbole d'inéquation: ici, ''plus ou égal'' veut dire que ta droite sera pleine dans le plan cartésien et que ta région-solution se trouve au dessus de ta droite (vers le haut)

En espérant avoir répondu à ta question, je te conseille de consulter cette fiche pour t'aider à comprendre le concept d'inéquation d'une droite et sa représentation graphique dans le plan cartésien: https://www.alloprof.qc.ca/fr/eleves/bv/mathematiques/le-demi-plan-et-l-ensemble-solution-m1534

Bon travail

Salut!

Une fraction irréductible est une fraction dont le numérateur et le dénominateur n'ont aucun diviseur commun (sauf 1). En d'autres mots, le numérateur et le dénominateur ne peuvent pas être simplifiés davantage.

Voici un exemple :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

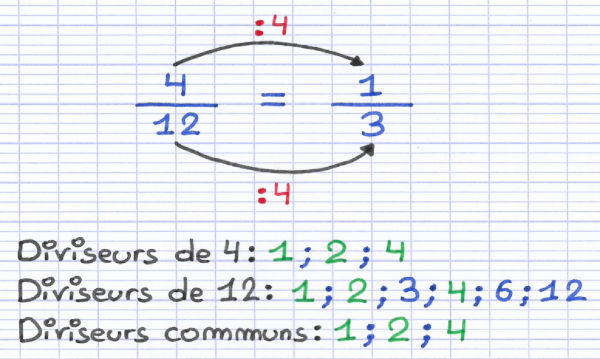
La fraction \(\frac{4}{12}\) n'est pas une fraction irréductible (donc c'est une fraction réductible, c'est-à-dire qui peut être réduite), puisque le numérateur et le dénominateur ont des diviseurs communs qui ne sont pas 1, soit 2 et 4.

Pour transformer la fraction \(\frac{4}{12}\) en une fraction irréductible, nous devons diviser le numérateur et le dénominateur par le plus grand diviseur commun (que l'on appelle le PGCD). Puisque le plus grand diviseur commun du numérateur 4 et du dénominateur 12 est 4, alors nous allons diviser ceux-ci par 4, ce qui nous donne \(\frac{1}{3}\).

Ainsi, \(\frac{4}{12}\) et \(\frac{1}{3}\) sont des fractions équivalentes (qui valent la même chose, qui sont égales), \(\frac{4}{12}\) est une fraction réductible et \(\frac{1}{3}\) est une fraction irréductible.

Voici une fiche sur cette notion pour plus d'exemples : Les fractions irréductibles | Primaire | Primaire | Alloprof

J'espère que c'est plus clair pour toi! :)

Salut à toi 😃

Tout d'abord, une fraction irréductible est une fraction dont son numérateur et son dénominateur n'ont plus aucun diviseur commun. C'est-à-dire qu'elles sont totalement simplifiées. Par exemple, 6/5 est une fraction irréductibles puisque 5 ne peut pas se diviser par 6. Mais, 4/8 n'est pas irréductible car 8 peut être divisé par 4. Donc, la fraction irréductible de 4/8 serait 1/2. Si tu souhaites plus d'informations, tu peux visiter cette fiche:

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Alloprof aide aux devoirs | Alloprof

https://www.alloprof.qc.ca/fr/eleves/bv/mathematiques/les-fractions-irreductibles-primaire-m1605

Grâce à ses services d’accompagnement gratuits et stimulants, Alloprof engage les…

J'espère que cela répond à ta question,

Bon courage! 😉

ne lâche pas 😉

Bonjour SourisJaune9883!

Merci d'avoir utilisé la zone d'entraide pour répondre à tes questions.

Tout d'abord, une fraction irréductible est une fraction dont son numérateur et son dénominateur n'ont plus aucun diviseur commun. C'est-à-dire qu'elles sont totalement simplifiées. Par exemple, 6/5 est une fraction irréductible, puisque 5 ne peut pas se diviser par 6. Cependant, 4/8 n'est pas irréductible, car 8 peut être divisé par 4. Donc, la fraction irréductible de 4/8 serait 1/2. Si tu souhaites plus d'informations, tu peux visiter cette fiche:

J'espère que cela répond à ta question,

Bon courage!

CielSage2034

BonjourPoissonRouge5231,

Une esquisse, c'est dessiner la fonction dans le plan cartésien. Donc, à l'aide d'une table de valeurs où tu choisis les valeurs de x, tu places les coordonnées obtenues afin de les relier pour représenter la fonction.

Ensuite, tu devras trouver, à l'aide ton graphique ou d'une démarche algébrique, le sommet, le zéro (abscisse à l'origine, i.e. le x quand y=0) et le signe de ta fonction (quand est-ce que la fonction est au-dessus de l'axe des x et en-dessous de l'axe des x). Pour le signe, l'information se lit par rapport à l'axe des abscisses.

Salut!

Avant de tracer la fonction, il faut d'abord s'assurer que nous avons bien la forme canonique de l'équation :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

On a l'équation :

k(x) = -3 [-2x-6] -2

Nous devons isoler le paramètre b afin d'obtenir la forme canonique. En isolant -2, nous obtenons :

k(x) = -3 [-2(x+3)] -2

On peut réécrire l'équation pour bien voir le signe négatif de la forme canonique devant le h :

k(x) = -3 [-2(x- -3)] -2

Nos paramètres sont donc : a=-3, b=-2, h=-3 et k=-2.

On est maintenant prêt à tracer la fonction! Pour ce faire, je t'invite à consulter la fiche suivante, elle explique la démarche à suivre pour tracer une fonction partie entière : Tracer une fonction en escalier (partie entière) | Secondaire | Alloprof

Et à revenir nous voir si tu as d'autres questions! :)

Dans chaque cas il y une unité de différence entre le numérateur et le dénominateur, c'est-à-dire dans tous le cas il te manque un morceau pour avoir le tout au complet. Ce morceau qui manque est plus petit quand le dénominateur est plus grand. Donc par exemple, la fraction 1/2 est plus petite que la fraction 2/3 car le morceau qui manque à 1/2 pour avoir le tout est plus grand que le morceau qui manque à 2/3 pour avoir le tout.