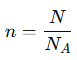Best Of
Re: Question
Bonjour CaribouJaune1036, merci d'utiliser la Zone d'entraide. Je vais t'expliquer ce que tu dois trouver au #2 pour la question 16.
On te demande de trouver le nombre de particules de substance dans chaque quantité de matière. Le mot particules réfère aux atomes ou aux molécules. Un exemple pourrait t'aider à comprendre.
Dans le A, on te dit qu'il y a 50,0 g de cuivre. Dans ce cas, on cherche combien il y a d'atomes de cuivre dans le 50,0g.
Pour t'y prendre, je te suggère de faire la formule suivante:
où
n: Nombre de moles ( tu as trouvé 0,79 mol)
N: Nombre de particules
NA: Nombre d'Avogadro (6,02 x 10²³)
Donc, si tu sais que NA est égal à 6,02 x 10²³ et que n est égal à 0,79 mol, tu peux maintenant trouver N qui est le nombre de particules, cuivre dans ton cas.
Je t'invite à consulter cette fiche https://www.alloprof.qc.ca/fr/eleves/bv/sciences/la-mole-s1115 ou à nous contacter si tu as d'autres questions.
DragonMagnifique5442
Re: Question
Bonjour.
On veut trouver le nombre de particules dans une substance. Puisque tu as trouvé qu'il y a 0,79 mol. On utilise la formule N= n x NA pour trouver le grand N.
n= nombre de mol
NA- Nombre Avogadro(6,022 x 10^23)
N'hésitez pas de demander des questions si vous ne comprenez pas.
Question
bonjour j'aimerais savoir comment transformer une vidéo en lien comme Ex: https://www.alloprof.qc.ca/fr/eleves/bv/jeux.
je vaudrais que sa sois rapide s'il vous plaît merci !
Question
Je me demandais pour mon cours de sciences sociales et droit puisque je ne trouve pas d’information sur le sujet si vous aviez une réponse à la question suivante?:
Aristote et la manière de cultiver la vertu.
cette question est si vague et sans définitions simple. Merci d’avance.
Marck
CCL secondaire 5
Re: Question
Salut à toi !
Merci pour ta question. :)
Je dois t'avouer que cela sort un peu de notre champ d'expertise ! Par contre, Tel-Jeunes a une super section sur l'amitié que tu pourrais consulter ! Tu pourras également t'adresser à un.e intervenant.e au besoin. :)
N'hésite surtout à nous réécrire si tu as d'autres questions !
Océane :)
Re: Question
Salut
En tout cas tu as de la chance ! :D
Sinon voici quelques liens si ça t'intéresse
Je sais que ça fait beaucoup 😅 mais en moins si ça t'intéresse tu es servi(e) !😁
PerleAdorable330